


所属成套资源:2021-2022学年七年级数学下学期重难点精品讲义(沪教版)
- 第14讲-全等三角形性质与判定(二)-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版) 试卷 2 次下载
- 第15讲-等腰三角形-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版) 试卷 3 次下载
- 第17讲-三角形与平行线-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版) 试卷 3 次下载
- 第18讲-三角形-单元综合测试-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版) 试卷 2 次下载
- 第19讲-平面直角坐标系-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版) 试卷 2 次下载
第16讲-等边三角形-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版)
展开这是一份第16讲-等边三角形-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版),文件包含第16讲-等边三角形解析版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx、第16讲-等边三角形原卷版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
第14讲-等边三角形
1.理解等边三角形是特殊的等腰三角形,是轴对称性图形;
2.掌握等边三角形的性质,能够较熟练地利用“等边对等角”及有关特征解决相关问题;
(以提问的形式回顾)
1. 等边三角形性质有哪些?
(1)具备等腰三角形的左右性质
(2)等边三角形的三条边都相等,三个内角都等于60°
2. 等边三角形的判定:
(1)三条边相等的三角形是等边三角形
(2)三个内角相等的三角形是等边三角形
(3)有一个内角是60°的等腰三角形是等边三角形
小练习
1.延长等边ΔABC的边BC到D,使CD = BC,那么ΔABD是 ( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形
2.如图,在ΔABC中,∠C = 120°,∠A = 45°,D在BC上,直线AD将这个三角形分成两个等腰三角形,则∠CDA的度数是 ( )
A、20° B、30°
C、45° D、15°
3.下列说法中错误的是 ( )
A、等腰三角形是锐角三角形 B、等腰直角三角形是直角三角形
C、等边三角形是等腰三角形 D、等边三角形是锐角三角形
4.D是等边ΔABC边AC上一点,∠ACE = ∠ABD,CE = BD,则ΔADE是 ( )
A、钝角三角形 B、直角三角形 C、任意等腰三角形 D、等边三角形
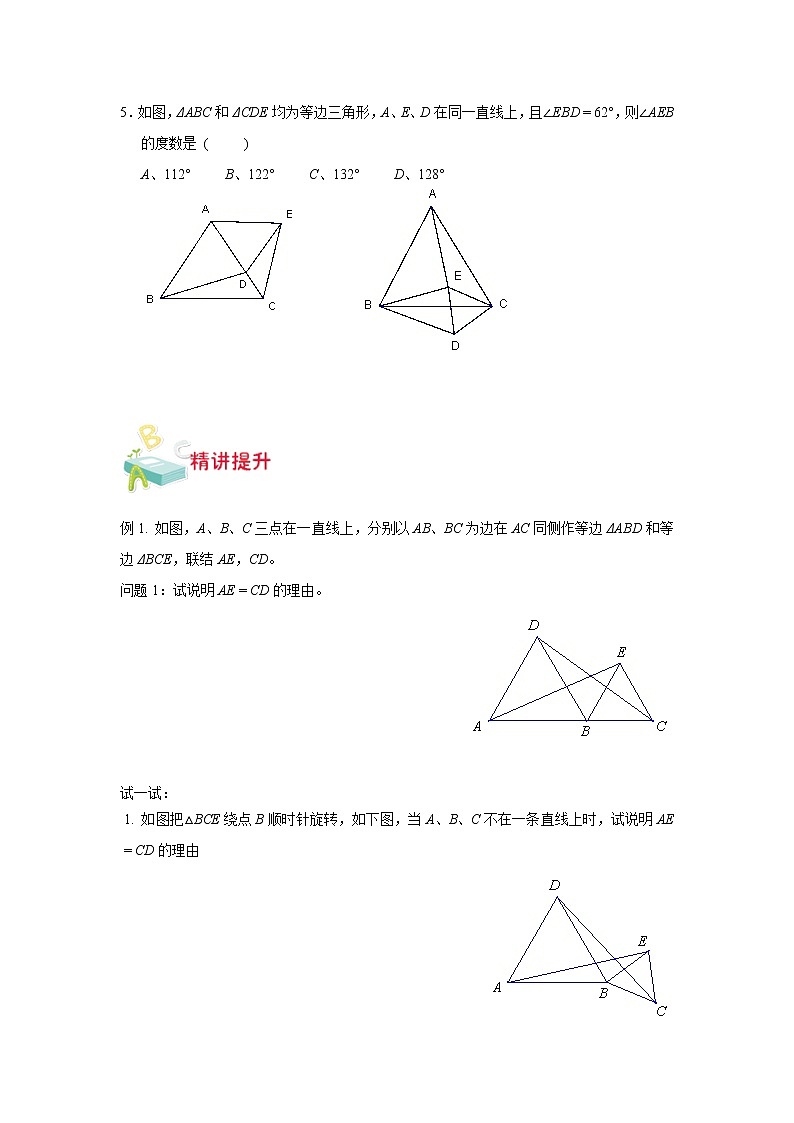
5.如图,ΔABC和ΔCDE均为等边三角形,A、E、D在同一直线上,且∠EBD = 62°,则∠AEB的度数是 ( )
A、112° B、122° C、132° D、128°
参考答案:1、A; 2、B; 3、A; 4、D; 5、B
(采用教师引导,学生轮流回答的形式)
例1. 如图,A、B、C三点在一直线上,分别以AB、BC为边在AC同侧作等边ΔABD和等边ΔBCE,联结AE,CD。
问题1:试说明AE = CD的理由。
解析:证明ΔABE≌ΔDBC(SAS)
试一试:
1. 如图把△BCE绕点B顺时针旋转,如下图,当A、B、C不在一条直线上时,试说明AE = CD的理由
解析:证明ΔABE≌ΔDBC(SAS)
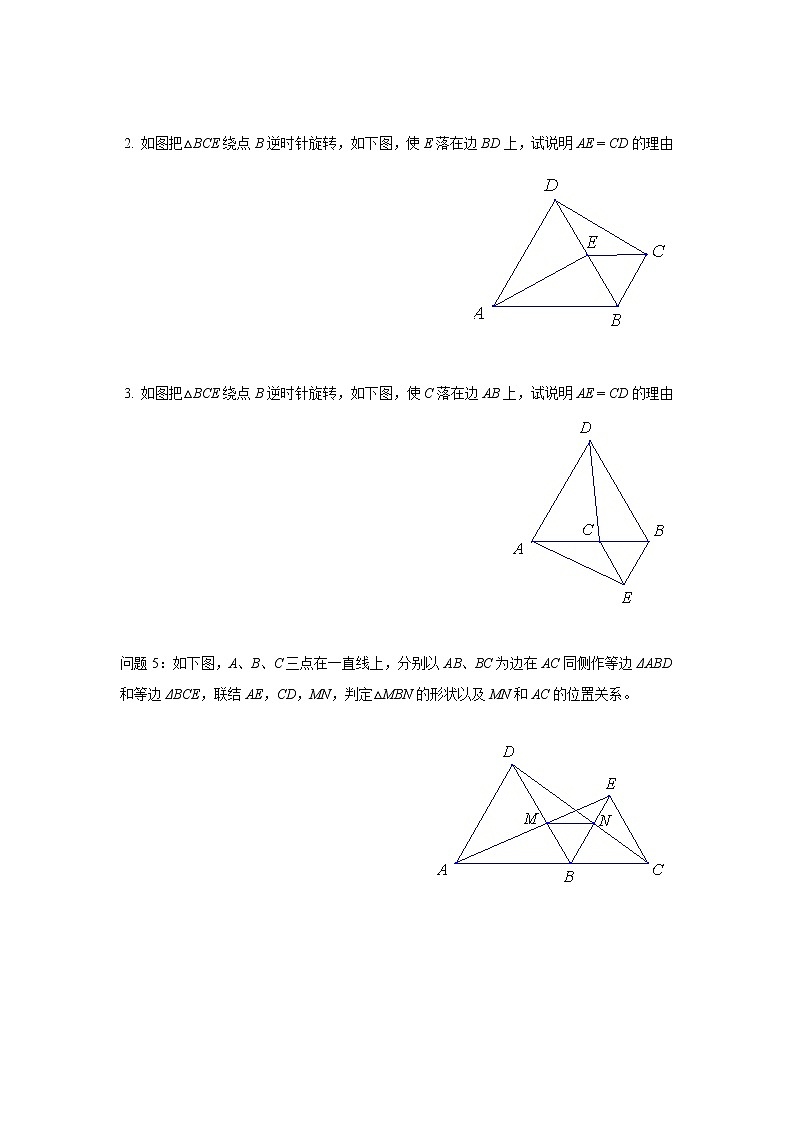
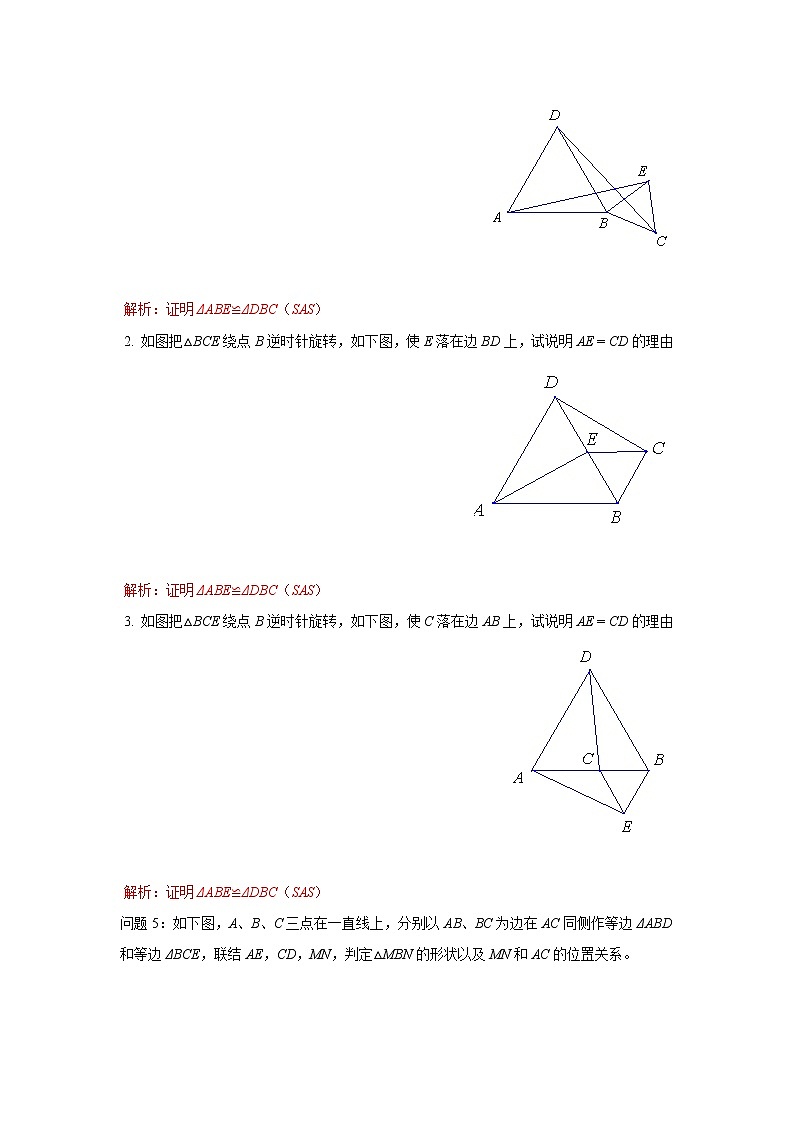
2. 如图把△BCE绕点B逆时针旋转,如下图,使E落在边BD上,试说明AE = CD的理由
解析:证明ΔABE≌ΔDBC(SAS)
3. 如图把△BCE绕点B逆时针旋转,如下图,使C落在边AB上,试说明AE = CD的理由
解析:证明ΔABE≌ΔDBC(SAS)
问题5:如下图,A、B、C三点在一直线上,分别以AB、BC为边在AC同侧作等边ΔABD和等边ΔBCE,联结AE,CD,MN,判定△MBN的形状以及MN和AC的位置关系。
解析:先证明ΔABE≌ΔDBC(SAS)得到∠BAE=∠BDC,
再证明ΔABM≌ΔDBN(ASA)得到BM=BN,所以△MBN为等边三角形,
MN∥AC
例2. 如图,在△中,已知,点、、分别在边、、上,且,.
(1)说明△与△全等的理由.
(2)如果△是等边三角形,那么△是等边三角形吗?试说明理由.
解 :(1)记,.
因为(三角形的一个外角等于与它不相邻的两个内角和),
即.
又因为(已知),
所以(等式性质).
因为(已知),
所以(等边对等角).
在△和△中,
所以△≌△(AAS),
(2)因为△≌△,
所以(全等三角形的对应边相等).
因为△是等边三角形(已知),
所以(等边三角形的每个内角等于60°).
因为(已知),
所以(等量代换).
所以△是等边三角形(有一个内角等于的等腰三角形是等边三角形).
例3. 如图,D为等边ΔABC内一点,DB=DA,BE=AB,∠DBE=∠DBC,求∠BED的度数。
解析:联结DC,先证明ΔACD≌ΔBCD(SSS) 得到∠ACD=∠BCD=30°
再证明ΔEBD≌ΔCBD(SAS)得到∠BED=∠BCD=30°
1.(2021·上海市风华初级中学七年级期末)下列说法中,正确的有( )
①都含有70°的两个直角三角形一定全等;
②都含有100°的两个等腰三角形一定全等;
③底边相等的两个等腰三角形一定全等;
④边长都为10cm的两个等边三角形一定全等;
⑤如果两个等腰三角形的腰长相等,且一腰上的高与另一腰的夹角也恰好相等,那么这两个等腰三角形全等.
A.0个 B.1个 C.2个 D.3个
【答案】C
【解析】
【分析】
利用全等三角形的判定方法判断即可得到结果.
【详解】
解:①都含有70°的两个直角三角形不一定相等,因为没有对应边相等,所以①错误;
②都含有100°的两个等腰三角形不一定相等,因为没有对应边相等,所以②错误;
③底边相等的两个等腰三角形不一定相等,因为没有对应角相等,所以③错误;
④边长都为10cm的两个等边三角形一定全等;
因为根据SSS或AAS或SAS或ASA可以判定两个三角形全等,所以④正确;
⑤如果两个等腰三角形的腰长相等,且一腰上的高与另一腰的夹角也恰好相等,那么这两个等腰三角形全等.
因为根据条件可以得出两个等腰三角形的底角,顶角对应相等,再根据SAS或AAS或ASA可以判定两个三角形全等,所以⑤正确;
所以正确的有④⑤这2个.
故选:C.
【点睛】
本题考查了全等三角形的判定,等腰三角形的性质,熟练掌握全等三角形的判定方法是解本题的关键.
2.(2020·上海市第十中学七年级阶段练习)在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个 B.3个 C.2个 D.1个
【答案】C
【解析】
【分析】
根据等边三角形的性质和定义,可得:有一个角为60°的等腰三角形是等边三角形;三个内角都相等的三角形为等边三角形;再由中线的性质和三角形内角和的定义可解答本题.
【详解】
解:①因为外角和与其对应的内角的和是180°,已知有一个外角是120°,即是有一个内角是60°,有一个内角为60°的等腰三角形是等边三角形.该结论正确;
②两个外角相等说明该三角形中两个内角相等,而等腰三角形的两个底角是相等的,故不能确定该三角形是等边三角形.该结论错误;
③等腰三角形的底边上的高和中线本来就是重合的,“有一边”可能是底边,故不能保证该三角形是等边三角形.该结论错误;
④三个外角都相等的三角形是等边三角形,说法正确,
正确的命题有2个,
故选:C.
【点睛】
本题考查等边三角形的判定,解题的关键是灵活运用的等边三角形的判定方法解决问题.
3.(2021·上海市文来中学七年级期中).如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )
A.3个 B.4个 C.5个 D.6个
【答案】D
【解析】
【详解】
∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
即AB=BC,BD=BE,∠ABE=∠CBD
∴△ABE≌△CBD,
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴△BGD≌△BFE,
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
∴△ABF≌△CGB,
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∵∠FHG+∠FBG=120°+60°=180°,
∴B、G、H、F四点共圆,
∵FB=GB,
∴∠FHB=∠GHB,
∴BH平分∠GHF,
∴题中①②③④⑤⑥都正确.
故选D.
点睛:本题主要考查对等边三角形的性质,全等三角形的判定和性质等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.
4.(2020·上海市徐汇中学七年级阶段练习)如图,将边长为6cm的等边△ABC沿BC边向右平移得到△DEF.平移后,如果四边形ABFD的周长是22cm,那么平移的距离应该是_______cm.
【答案】2
【解析】
【分析】
根据平移的性质,得;根据等边三角形的性质,得,结合题意,通过列一元一次方程并求解,即可得到答案.
【详解】
根据题意,得:,
∴四边形ABFD的周长
∴
故答案为:2.
【点睛】
本题考查了等边三角形、平移的知识;解题的关键是熟练掌握等边三角形、平移的性质,从而完成求解.
5.(2021·上海徐汇·七年级阶段练习)如图,三角形和三角形是等边三角形,三角形绕点顺时针旋转后得三角形,为45度,则__度.
【答案】75
【解析】
【分析】
根据等边三角形的性质以及旋转的性质进行解答即可.
【详解】
解:如图,是等边三角形,
,
绕点顺时针旋转后得,
,
,
,
,
故答案为:75.
【点睛】
本题考查了等边三角形的性质,旋转的性质以及三角形内角和定理的应用,熟练掌握旋转后的对应角相等是解本题的关键.
6.(2021·上海市培佳双语学校七年级期中)用一根长12cm的铁丝围成一个等边三角形,那么这个等边三角形的边长为 ___cm.
【答案】4
【解析】
【分析】
根据等边三角形的定义“三条边都相等的三角形”即可求出答案.
【详解】
根据等边三角形的三条边相等可知其边长cm.
故答案为:4.
【点睛】
本题考查等边三角形的定义.掌握其定义是解答本题的关键.
7.(2019·上海浦东新·七年级期末)已知°,点在的内部,点与点关于对称,点与点关于对称,若,则______.
【答案】5
【解析】
【分析】
连接OP,根据轴对称的性质可得OP1=OP=OP2,∠BOP=∠BOP1,∠AOP=∠AOP2,然后求出∠P1OP2=2∠AOB=60°,再根据有一个角是60°的等腰三角形是等边三角形判定.
【详解】
解:如图,连接OP,
∵P1与P关于OB对称,P2与P关于OA对称,
∴OP1=OP=OP2,∠BOP=∠BOP1,∠AOP=∠AOP2,
∴OP1=OP2,
∠P1OP2=∠BOP+∠BOP1+∠AOP+∠AOP2=2∠BOP+2∠AOP=2∠AOB,
∵∠AOB=30°,
∴∠P1OP2=60°,
∴△P1OP2是等边三角形.
∴P1P2 =OP2=OP=5,
故答案为:5.
【点睛】
本题考查了轴对称的性质,等边三角形的性质和判定,熟练掌握轴对称的性质求出△P1OP2的两边相等且有一个角是60°是解题的关键,作出图形更形象直观.
8.(2019·上海市民办新竹园中学七年级期中)在△ABC中, ∠C=60º, BC= 6, AC= 4, AD是高, 将△ACD沿着AD翻折, 点C落在点E上, 那么BE的长是_________;
【答案】2
【解析】
【分析】
先解直角△ACD,得出CD=2,再根据翻折的性质得到DE=CD=2,那么由BE=BC-CD-DE即可求解.
【详解】
如图,在直角△ACD中,
∵∠ADC=90°,∠C=60°,
∴∠DAC=30°,
∴CD=AC=×4=2.
∵将△ACD沿着AD翻折,点C落在点E上,
∴DE=CD=2,
∵BC=6,
∴BE=BC-CD-DE=6-2-2=2.
故答案是:2.
【点睛】
考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等.也考查了直角三角形的性质.
9.(2018·上海·华东理工大学附属中学七年级阶段练习)在同一平面内,将一副直角三角板ABC和EDF如图放置(∠C=60°,∠F=45°),其中直角顶点D是BC的中点,点A在DE上,则∠CGF=_____°.
【答案】15°
【解析】
【分析】
根据直角三角形斜边中线等于斜边一半证明△ADC是等边三角形,得∠EAG=120°,在△AEG中求出∠AGE=15°即可解题.
【详解】
解:由题得:AD是直角三角形斜边中点,
∴AD=BC=CD=BD
∵∠C=60°,∠F=45°,
∴△ADC是等边三角形,
∴∠DAC=60°,
∴∠EAG=125°,
∴∠CGF=∠AGE=15°.
【点睛】
本题考查了特殊的直角三角形,斜边中线的性质,属于简单题,证明△ADC是等边三角形是解题关键.
10.(2021·上海嘉定·七年级期末)在等边三角形的两边、所在直线上分别有两点、,为外一点,且,,.探究;当点、分别在直线、上移动时,,,之间的数量关系.
(1)如图①,当点、在边、上,且时,试说明.
(2)如图②,当点、在边、上,且时,还成立吗?
答:________(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点、分别在边、的延长线上时,请直接写出,,之间的数量关系.
【答案】(1)见解析
(2)一定成立
(3),理由见解析
【解析】
【分析】
(1)由PM=PN,∠MPN=60°,可证得△MPN是等边三角形,又由△ABC是等边三角形,CP=BP,易证得Rt△BPM≌Rt△CPN,然后由直角三角形的性质,即可求得BM、NC、MN之间的数量关系 BM+NC=MN;
(2)在CN的延长线上截取CH=BM,连接PH.可证△PBM≌△PCH,即可得PM=PH,易证得∠CPN=∠MPN=60°,则可证得△MPN≌△HPN,然后由全等三角形的性质,即可得结论仍然成立.
(3)在上截取,连接,分别证明和即可得到结论
(1)
∵PM=PN,∠MPN=60°,
∴△MPN是等边三角形,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,
∵BP=CP,∠BPC=120°,
∴∠PBC=∠PCB=,
∴∠MBP=∠NCP=60°+30°=90°
∵PM=PN,BP=CP,
∴Rt△BPM≌Rt△CPN(HL),
∴∠BPM=∠CPN=30°,BM=CN,
∴PM=2BM,PN=2CN,
∴MN=2BM=2CN=BM+CN;
(2)
延长到,使,连接,
由(1 )知,
,
,
在和中,
,
,
,,
,,
,
在和中,
,
,
,
,
.
故答案为:一定成立.
(3)
在上截取,连接,
在和中,
,
,
,,
,
,
,
,
在和中,
,
,
,
,
.
【点睛】
此题考查了全等三角形的判定与性质,等边三角形,直角三角形,等腰三角形的性质等知识.解题的关键是注意数形结合思想的应用与辅助线的作法.
11.(2021·上海市向东中学七年级期末)如图,在等边△ABC中,边AB=6厘米,若动点P从点C开始,按C→B→A→C的路径运动,且速度为1厘米/秒,设点P的运动时间为秒.
(1)当t=3秒时,判断AP与BC的位置关系,并说明理由.
(2)当△PBC的面积为△ABC面积的一半时,求t的值.
(3)另有一点Q,从点C开始,按C→A→B→C的路径运动,且速度为1.5厘米/秒,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
【答案】(1)AP⊥BC,证明见解析
(2)9秒或15秒
(3)秒或秒
【解析】
【分析】
(1)根据等边三角形的性质即可得到结论;
(2)根据等边三角形的性质和三角形的面积公式即可得到结论;
(3)根据等边三角形的性质和三角形的周长公式即可得到结论.
(1)
解:当t=3秒时,CP=3×1=3(cm),
∵在等边△ABC中,AB=6cm,
∴BC=AB=6cm,
∴此时,P为BC的中点,
∴AP为等边△ABC的中线,
∴AP⊥BC;
(2)
解:∵由题意得:,
∴当P为AB中点时,满足题意,
此时,P点运动路程为:BC+BP=6+3=9(cm),
∴P点运动时间为:9÷1=9(秒);
当P为AC中点时,满足题意,
此时,P点运动路程为:BC+AB+AP=6+6+3=15(cm),
∴P点运动的时间为:15÷1=15(秒),
∴综上,t的值为9秒或15秒;
(3)
解:∵点P的速度为1厘米/秒,点Q的速度为1.5厘米/秒,
∴由题意得:当时,点P在BC上,点Q在AC上,
∴PC+CQ=t+1.5t=2.5tcm,
,
∴2.5t=9,
解得:,符合;
当时,点Q在AB上,点P在BC上,
,,
.
,解得:,
∴不符合,舍去;
当时,P、Q都在AB上,不符合题意;
当时,点Q在BC上,点P在AB上,
∴BP=(t-6)cm,BQ=(1.5t-12)cm,
,,
解得:,符合,
∴综上,符合条件的t的值为:秒或秒.
【点睛】
本题考查了等边三角形的性质,动点问题的解决方法,用时间t表示出各时段的线段的长度列出方程求解是解题的关键.
12.(2021·上海市市西初级中学七年级期末)在中,,,以BC、AC为边向外作等边和等边.
(1)如图1,连接AD、BE,AD与BE相交于点O.
①说明的理由.
②______°.(直接填答案)
(2)如图2,连接DE,交BC于点F,DF与EF相等吗?为什么?
【答案】(1)①见解析;②120
(2),理由见解析
【解析】
【分析】
(1)①在等边三角形和中,,,,,即,证得,得到.
②设AD与BC交于H,由得到,,,,,得到.
(2)作交BC于M,交AC于N,由于和是等边三角形,证得∠DCA=90°,,得到,,=∠CEM,证得,得CB=EM,,,,DCF=∠EMF,,得到.
(1)
解:①∵和是等边三角形,
∴,,,
∴,
即,
在和中,
,
∴,
∴.
②设AD与BC交于H,如图3,
∵,
∴,
∵,
,
,
∴,
∴.
(2)
解:;理由如下,
过E作交BC于M,交AC于N,如图4,
∵和是等边三角形,
∴,,
,
∵,
∴,
,
∵于N,,
∴,,
∴,
在和中,
,
∴,
∴,
∴,
∵,
∴,
∴,
在和,
,
∴,
∴.
【点睛】
本题主要考查了等边三角形的性质和全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具;在判定三角形全等时,关键是选择恰当的判定条件.
13.(2021·上海市培佳双语学校七年级期中)如图,已知是等边三角形内一点,是线段延长线上一点,且,,求的度数.
【答案】60
【解析】
【分析】
先证是等边三角形,得出是等边三角形,再证,得,从而得出∠BOC的大小.
【详解】
∵∠AOB=120°,∴∠AOD=60°
∵AO=OD,∴△AOD是等边三角形
∴,
∵△ABC是等边三角形,∴∠BAC=60°,AB=AC
∴∠BAC=∠OAD,∴∠BAO+∠OAC=∠OAC+∠CAD
∴∠BAO=∠CAD
在△BAO和△CAD中
∴
∴
∴
【点睛】
本题考查全等的证明和等边三角形的性质和证明,解题关键是证.
14.(2021·上海市久隆模范中学七年级期末)如图,是绕点逆时针方向旋转60°后所得的图形,点恰好在上,,则∠D的度数是( ).
A.40° B.50° C.60° D.70°
【答案】B
【解析】
【分析】
先根据旋转的性质可得,再根据等边三角形的判定与性质可得,从而可得,然后根据角的和差可得,最后根据三角形的内角和定理即可得.
【详解】
解:由旋转的性质得:,
是等边三角形,
,
,
,
,
,
故选:B.
【点睛】
本题考查了旋转的性质、等边三角形的判定与性质、三角形的内角和定理等知识点,熟练掌握旋转的性质是解题关键.
15.(2021·上海闵行·七年级期末)如图,已知点B、C、E在一直线上,、都是等边三角形,联结和,与相交于点F,与相交于点G,下列说法不一定正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】
利用等边三角形的性质和“SAS”证明可得A选项;可利用“ASA”证明可得C、D选项,利用排除法求解即可.
【详解】
解:∵、都是等边三角形,
∴,=60°,,
∴∠ACB+∠ACD=∠ECD+∠ACD,即∠ACE=∠BCD,
∴(SAS),
∴BD=AE,(故A正确);
∴∠AEC=∠BDC,又,,
∴(ASA),
∴EG=FD,(故C正确),
FC=GC,(故D正确)
由于B项不能由已知条件得到,故B错误,
故选:B.
【点睛】
本题考查等边三角形的性质、全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解答的关键.
16.(2019·上海长宁·七年级期末)下列所叙述的图形中,全等的两个三角形是( )
A.含角的两个直角三角形 B.腰对应相等的两个等腰三角形
C.边长均为5厘米的两个等边三角形 D.一个钝角对应相等的两个等腰三角形
【答案】C
【解析】
【分析】
综合运用判定方法判断.根据已知条件,结合全等的判定方法逐一验证.
【详解】
解:A.两个含60°角的直角三角形,缺少对应边相等,所以不是全等形;
B. 腰对应相等的两个等腰三角形,夹角不一定相等,所以不是全等形;
C. 等边三角形的每个内角都等于60°,所以边长均为5厘米的两个等边三角形,各条边相等,各个角也相等,是全等三角形;
D. 一个钝角相等的两个等腰三角形.缺少对应边相等,不是全等形.
故选C
【点睛】
本题考查了三角形全等的判定方法;需注意:判定两个三角形全等时,必须有边的参与,还要找准对应关系.
17.(2021·上海市西南模范中学七年级期末)如图,已知等边中,点D为边BC上一点,延长AC至点E,使得CE=BD,联结ED并延长交边AB于点F,联结AD,若,则的度数为________(用含的式子表示).
【答案】
【解析】
【分析】
根据为等边三角形,得到AB=BC,,过点作,则,则为等边三角形,可证AN=CD,再证,根据全等三角形的性质即可求解.
【详解】
解: 过点作,
∵为等边三角形,
∴AB=BC,,
∵,
∴,
∴为等边三角形,
∴DN=BD=BN,,
∴,
∴BC-BD=AB-BN,即AN=CD,
在和中,
∴,
∴,
∵,
∴.
【点睛】
本题考查全等三角形的判定和性质、等边三角形的判定和性质.本题的关键是做出辅助线构造等边三角形.
18.(2021·上海杨浦·七年级期末)如图,已知直线,等边三角形的顶点分别在直线上,如果边与直线的夹角,那么边与直线的夹角______度.
【答案】
【解析】
【分析】
根据平行线的性质与等边三角形的性质可得,继而可得,即可求得
【详解】
解:是等边三角形,
,
直线,
,
,
,
,
故答案为:34.
【点睛】
本题考查了等边三角形的性质、平行线的性质等知识;熟练掌握等边三角形的性质和平行线的性质,证出是解题的关键.
19.(2021·上海闵行·七年级期末)在中,如果,,那么的形状为______.
【答案】等边三角形
【解析】
【分析】
根据三个角相等的三角形是等边三角形证明即可.
【详解】
在中,由得,
又∵,
∴,
∴是等边三角形.
故答案为:等边三角形.
【点睛】
本题考查了等腰三角形的性质,以及等边三角形的判定,熟练掌握三个角相等的三角形是等边三角形是解答本题的关键.
20.(2021·上海浦东新·七年级期末)在Rt△ABC中,∠C=90°,将这个三角形折叠,使点B与点A重合,折痕交边AB于点M,交BC于点N,如果BN=2NC,那么∠ABC=_____度.
【答案】30
【解析】
【分析】
根据折叠的性质得到∠1=∠B,NA=NB,求出∠ANC=60°,再利用三角形的外角定理得∠2=2∠B,然后根据直角三角形的性质即可得到结论.
【详解】
解:如图,
∵将这个三角形折叠,使点B与点A重合,折痕交AB于点M,交BC于点N,
∴∠1=∠B,NA=NB,
∵BN=2NC,
∴AN=2NC,
∵∠C=90°,
∴∠CAN=30°,
∴∠ANC=60°,
∵∠2=2∠B,
∴∠B=30°,
故答案为:30.
【点睛】
本题考查了折叠的性质:折叠前后两图形全等,即得到对应角相等,对应线段相等.也考查了含30度的直角三角形三边的关系.
21.(2021·上海·七年级期末)若把一个边长为2厘米的等边向右平移a厘米,则平移后所得三角形的周长为__________厘米.
【答案】6
【解析】
【分析】
平移不改变三角形的周长,求出原来的周长即可.
【详解】
解:原三角形的周长是:,
平移后的三角形周长不变,还是.
故答案是:6.
【点睛】
本题考查图形的平行,解题的关键是掌握图形平移的性质.
22.(2018·上海金山·七年级期末)如图,已知是等边三角形,D为BC延长线上一点,CE平分,,,那么AE的长度是______.
【答案】7
【解析】
【分析】
先利用等边三角形的性质得AB=AC,∠B=∠ACB=60°,再根据角平分线的定义得到∠ACE=60°,然后根据“SAS”判断△ABD≌△ACE,从而得到AE=AD=7.
【详解】
∵△ABC为等边三角形,∴AB=AC,∠B=∠ACB=60°,∴∠ACD=120°.
∵CE平分∠ACD,∴∠ACE=∠ACD=60°.
在△ABD和△ACE中,
∵,∴△ABD≌△ACE,∴AE=AD=7.
故答案为7.
【点睛】
本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了等边三角形的性质.
23.(2021·上海市久隆模范中学七年级期末)如图,在等边三角形中,、分别是边、上的动点且,连接、,记交点为,试问、所成的的大小有无变化?说明理由.
【答案】的大小无变化,理由见解析.
【解析】
【分析】
先根据等边三角形的性质可得,再根据三角形全等的判定定理证出,根据全等三角形的性质可得,然后根据三角形的外角性质可得,由此即可得出结论.
【详解】
解:的大小无变化,理由如下:
是等边三角形,
,
在和中,,
,
,
,
,
即的大小无变化.
【点睛】
本题考查了等边三角形的性质、三角形全等的判定定理与性质等知识点,正确找出两个全等三角形是解题关键.
24.(2021·上海市徐汇中学七年级期末)如图,点D是等边△ABC边BA延长线上一点,,且,联结CD、CE.
(1)试说明:△BDC与△AEC全等的理由.
(2)试说明:△CDE是等边三角形的理由.
【答案】(1)理由见解析
(2)理由见解析
【解析】
【分析】
(1)证和,得到;
(2)根据,得到,,再证,则△CDE为等边三角形.
(1)
解:∵△ABC为等边三角形,
∴,,
∵,
∴,
∴,
在△BDC与△AEC中,
,
.
(2)
解:由(1)可知,
∴,,
则,
∴,
∴,
则△CDE为等边三角形.
【点睛】
本题考查全等三角形的判定和性质、等边三角形的判定和性质.有一个角为的等腰三角形是等边三角形.
25.(2021·上海·华东理工大学附属中学七年级期末)如图,,,,且、、三点在一条直线上,若.
(1)与是否全等,请说明理由.
(2)是否是等边三角形,如果是.请说明理由.
(3)是否成立,如果成立请说明理由.
【答案】(1);证明见解析
(2)是等边三角形;证明见解析
(3)成立;证明见解析
【解析】
【分析】
(1)根据AAS证明△ABD与△ACE全等即可;
(2)由△ABD与△ACE全等可得AB=AC,再根据即可证得;
(3)利用全等三角形的性质和等边三角形的判定和性质解答即可.
(1)
解:与全等;
理由如下:
∵,
∴,即,
在与中,
,
∴;
(2)
解:∵,
∴,
又∵,
∴是等边三角形;
(3)
解:成立,
理由如下:
∵,
∴,
∵是等边三角形,
∴,
∴,即.
【点睛】
本题考查了三角形全等的判定及性质,等边三角形的判定及性质,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
26.(2020·上海外国语大学闵行外国语中学七年级期末)如图,已知,△ABC和△ADE都是等边三角形,连接BD、CE.
(1)说明的理由;
(2)延长BD,交CE于点F,求∠BFC的度数.
【答案】(1)见解析;(2)60°.
【解析】
【分析】
(1)证明△ABD≌△ACE即可得到结论;
(2)由△ABD≌△ACE得到∠ABD=∠ACE,根据∠ABC=∠ACB=60°推出∠FBC+∠ACB+∠ACF=∠ABC+∠ACB=120°,再根据三角形内角和定理求出∠BFC的度数.
【详解】
(1)证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE;
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠ABC=∠ACB=60°,
∴∠FBC+∠ACB+∠ACF=∠ABC+∠ACB=120°,
∴∠BFC=180°-(∠ABC+∠ACB)=60°.
【点睛】
此题考查三角形全等的判定及性质,等边三角形的性质,三角形内角和定理,熟记三角形全等的判定定理,根据题意准确证明△ABD≌△ACE是解题的关键.
27.如图,等边△中,点在边上,CE∥AB,且CE=AD,
(1)△是什么特殊三角形,请说明理由.
(2)如果点在边的中点处,那么线段与有怎样的位置关系,请说明理由.
解: (1)△是等边三角形.
说理如下:
记,,
因为△是等边三角形(已知),
所以(等边三角形的三边都相等),
(等边三角形的每个内角都等于).
因为(已知),
所以(两直线平行,内错角相等).
所以(等量代换)
在△和△中,
所以△≌△(SAS),
得(全等三角形的对应角相等),
(全等三角形的对应边相等)
又因为
所以
即
所以△是等边三角形(有一个内角等于的等腰三角形是等边三角形)
(2)线段与的位置关系是:
说理如下:
因为,
所以(等腰三角形的三线合一)
因为
所以
又因为
所以(等腰三角形的三线合一)
相关试卷
这是一份第3讲-实数的运算-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版),文件包含第3讲-实数的运算解析版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx、第3讲-实数的运算原卷版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
这是一份第6讲-相交线-【同步优课】2022年七年级数学下学期重难点精品讲义(沪教版),文件包含第6讲-相交线解析版-同步优课2022年七年级数学下学期重难点精品讲义沪教版docx、第6讲-相交线原卷版-同步优课2022年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
这是一份第5讲-实数 单元综合测试-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版),文件包含第5讲-实数单元综合测试解析版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx、第5讲-实数单元综合测试原卷版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。












