2021-2022学年陕西省咸阳市泾阳县七年级（下）期末数学试卷-（含解析）

2021-2022学年陕西省咸阳市泾阳县七年级（下）期末数学试卷

一、选择题（本大题共8小题，共24分。在每小题列出的选项中，选出符合题目的一项）

1.    计算：(    )

A.  B.  C.  D.

2.    下列“表情图”中，属于轴对称图形的是(    )

A.  B.  C.  D.

3.    如图，，直角三角尺的直角顶点在上，如果，那么的度数为(    )

A.
B.
C.
D.

4.    变量与之间的关系式是，当自变量时，因变量的值是(    )

A.  B.  C.  D.

5.    计算：(    )

A.  B.  C.  D.

6.    下列说法正确的是(    )

A. 长度为、和的三条线段首尾相接可以组成三角形
B. 面积相等的两个三角形全等
C. 两直线被第三条直线所截，同位角相等
D. 等角的补角相等

7.    如图，在中，，平分，于如果，那么等于(    )

A.
B.
C.
D.

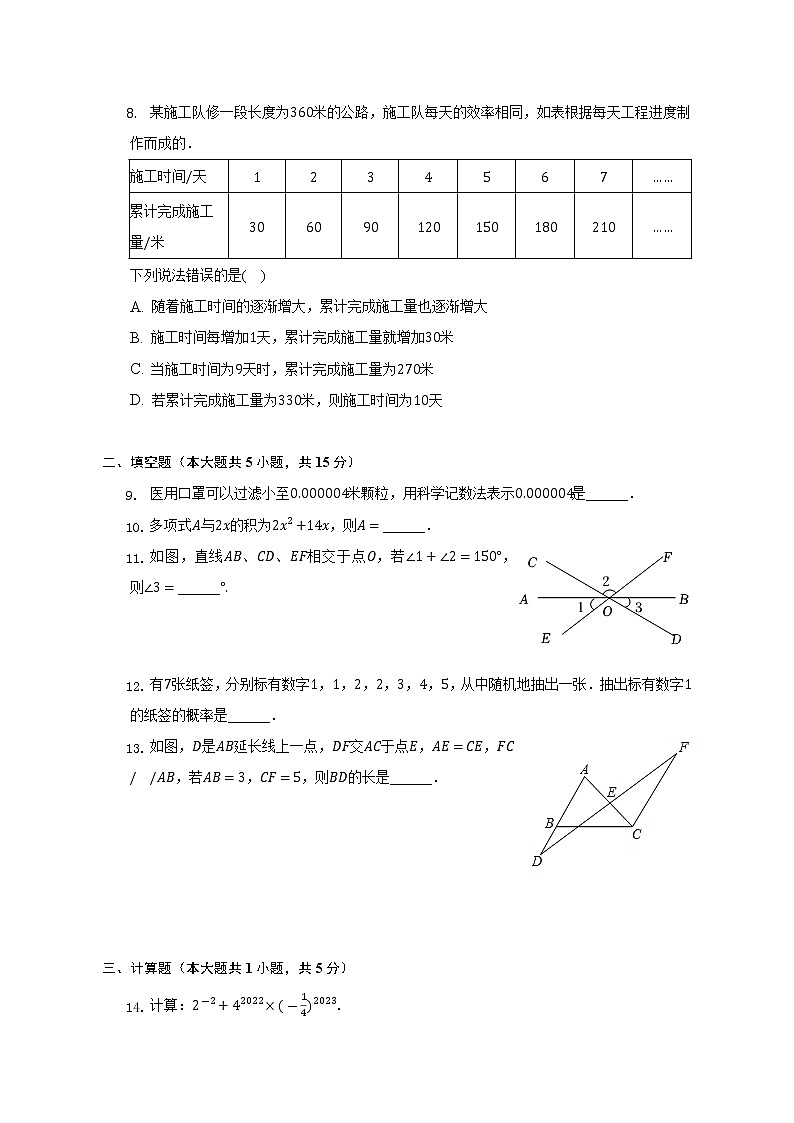
8.    某施工队修一段长度为米的公路，施工队每天的效率相同，如表根据每天工程进度制作而成的．

下列说法错误的是(    )

A. 随着施工时间的逐渐增大，累计完成施工量也逐渐增大
B. 施工时间每增加天，累计完成施工量就增加米
C. 当施工时间为天时，累计完成施工量为米
D. 若累计完成施工量为米，则施工时间为天

二、填空题（本大题共5小题，共15分）

9.   医用口罩可以过滤小至米颗粒，用科学记数法表示是______．
10. 多项式与的积为，则______．
11. 如图，直线、、相交于点，若，则______

12. 有张纸签，分别标有数字，，，，，，，从中随机地抽出一张．抽出标有数字的纸签的概率是______．
13. 如图，是延长线上一点，交于点，，，若，，则的长是______．

三、计算题（本大题共1小题，共5分）

14. 计算：．

四、解答题（本大题共12小题，共76分。解答应写出文字说明，证明过程或演算步骤）

15. 本小题分
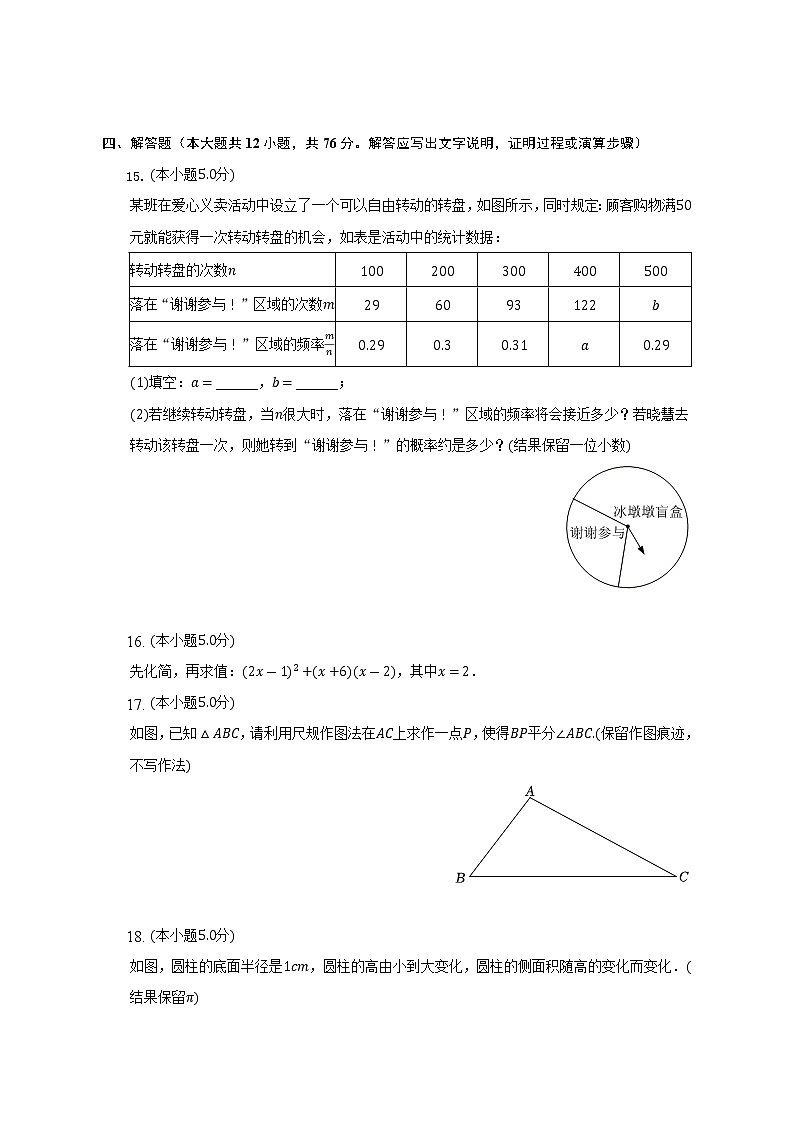
    某班在爱心义卖活动中设立了一个可以自由转动的转盘，如图所示，同时规定：顾客购物满元就能获得一次转动转盘的机会，如表是活动中的统计数据：

填空：______，______；
若继续转动转盘，当很大时，落在“谢谢参与”区域的频率将会接近多少？若晓慧去转动该转盘一次，则她转到“谢谢参与”的概率约是多少？结果保留一位小数

16. 本小题分
    先化简，再求值：，其中．
17. 本小题分
    如图，已知，请利用尺规作图法在上求作一点，使得平分保留作图痕迹，不写作法

18. 本小题分
    如图，圆柱的底面半径是，圆柱的高由小到大变化，圆柱的侧面积随高的变化而变化．结果保留
    在这个变化过程中，自变量和因变量各是什么？求圆柱的侧面积与圆
    柱的高之间的关系式；
    当圆柱的高为时，圆柱的侧面积是多少？

19. 本小题分
    如图，的顶点均在网格的格点上，与关于直线对称，点、、的对应点分别是、、．
    在图中画出；
    点与点关于直线对称，请画出直线．

20. 本小题分
    如图，在中，平分交于点，的垂直平分线交于点，交于点，，，求的度数．

21. 本小题分
    在学习完“探索三角形全等的条件”一节后，小丽总结出很多全等三角形的模型，她设计了以下问题给同桌解决：如图，做一个“”字形框架，，足够长，于点，于点，她在框架里放了两根长度相等的木条、，且，点、、分别在、、上，若，求的长．

22. 本小题分
    如图，有一块长方形板材，长为，宽比长少，若扩大板材，将其长和宽都增加．
    板材原来的面积即长方形的面积是多少平方厘米？
    板材面积增加后比原来多多少平方厘米？

23. 本小题分
    某中学七年级开展了“双减”下劳动实践活动，组织学生到实践基地割麦．张敏与同学从学校出发到实践基地，割完麦后，按原路返回．途中到小卖部买水，然后返回学校，张敏与同学离学校的距离米与所用时间分钟之间的关系如图所示．学校、小卖部、实践基地在同一直线上．
    学校到实践基地的距离为______，小卖部到实践基地的距离为______；
    张敏与同学在实践基地停留了多长时间？他们在小卖部买水用了多长时间？
    若他们上午：从学校出发，那么他们几点回到学校？

24. 本小题分
    如图，直线分别交直线、于点、，平分交于点，点是射线上一点，延长到点，使得，连接．
    若，，求的度数；
    若，，判断直线与是否平行？并说明理由．

25. 本小题分
    在一个不透明的袋子中装了个红球和个白球，这些球除颜色外都相同．
    下列事件中：不可能事件是______，必然事件是______，随机事件是______；填序号
    从袋子中同时摸出个球都是红球；
    从袋子中摸出个球是黑球；
    从袋子中同时摸出个球至少有一个是白球．
    求从袋子中随机摸出个球是红球的概率；
    小宇从袋子中取出个白球，同时又放入相同数目的红球，发现随机摸出一个球是红球的概率为，求的值．
26. 本小题分
    如图，已知是等腰三角形，，是锐角，点在边上，点在边上点、点不与所在线段端点重合，，连接，，射线，延长交射线于点，点在的延长线上，且．
    与全等吗？请说明理由；
    请求出的度数．用含的代数式表示

答案和解析

1.【答案】 

【解析】解：，
故选：．
根据零指数幂的意义计算即可．
本题考查零指数幂的意义，掌握零指数幂的意义是求解本题的关键．
 

2.【答案】 

【解析】解：不属于轴对称图形，故错误；
不属于轴对称图形，故错误；
不属于轴对称图形，故错误；
属于轴对称图形，故正确；
故选：．
根据轴对称图形的概念进行判断即可．
本题考查的是轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
 

3.【答案】 

【解析】解：如图：

，，
，
，
，
故选：．
根据已知先求出，然后利用平行线的性质，即可解答．
本题考查了平行线的性质，余角和补角，熟练掌握平行线的性质是解题的关键．
 

4.【答案】 

【解析】解：把代入中得：


，
故选：．
根据题意把代入中，进行计算即可解答．
本题考查了函数值，准确熟练地进行计算是解题的关键．
 

5.【答案】 

【解析】解：

．
故选：．
先算积的乘方，再算单项式乘单项式即可．
本题主要考查积的乘方，单项式乘单项式，解答的关键是对相应的运算法则的掌握．
 

6.【答案】 

【解析】解：，不符合三角形三边关系定理，不能组成三角形，故本选项不符合题意；
B.当一个三角形的底边是，这边上的高是，而另一个三角形的底边是，对应的高是，此时两三角形的面积相等，但两三角形不一定全等，故本选项不符合题意；
C.只有两条平行线被第三条直线所截，同位角才相等，故本选项不符合题意；
D.等角的补角相等，故本选项符合题意；
故选：．
根据三角形三边关系定理即可判断选项A；根据全等三角形的判定即可判断选项B；根据平行线的性质即可判断选项C；根据补角的性质即可判断选项D．
本题考查了全等三角形的判定，平行线的性质，三角形三边关系定理等知识点，能熟记全等三角形的判定、平行线的性质、三角形三边关系定理是解此题的关键．
 

7.【答案】 

【解析】解：，
，
又平分，，
，
，
，
，
故选：．
利用角平分线的性质，得到，所以，问题即可解决．
本题考查了角平分线的性质，利用角平分线的性质，得到，将转化成，是解决问题的关键．
 

8.【答案】 

【解析】解：根据表格可知，随着施工时间增大，累计完成施工量也逐渐增大，
故A选项不符合题意；
根据表格可知，施工时间每增加天，累计完成施工量就增加米，
故B选项不符合题意；
根据表格可知，施工时间为天时，累计完成施工量为米，
故C选项不符合题意；
当累计完成施工量为米时，天，
施工时间是天，
故D选项符合题意，
故选：．
根据表格依次进行判断即可．
本题考查了函数的表示方法，理解表格上各数据的含义是解题的关键．
 

9.【答案】 

【解析】解：．
故答案为：．
绝对值小于的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为，其中，为由原数左边起第一个不为零的数字前面的的个数所决定．
 

10.【答案】 

【解析】解：由题意得：


．
故答案为：．
根据题意可列出相应的式子，再运算即可得解．
本题主要考查多项式除以单项式，解答的关键是对多项式除以单项式的法则的掌握与运用．
 

11.【答案】 

【解析】解：，，
，
，
．
故答案为：．
根据平角的定义可以求出，再根据对顶角的性质求出即可．
本题考查了对顶角的性质，对顶角的性质：对顶角相等．邻补角、对顶角成对出现，在相交直线中，一个角的邻补角有两个．邻补角、对顶角都是相对与两个角而言，是指的两个角的一种位置关系．它们都是在两直线相交的前提下形成的．
 

12.【答案】 

【解析】解：从中随机地抽出一张共有种等可能结果，其中抽出标有数字的纸签的有种结果，
从中随机地抽出一张．抽出标有数字的纸签的概率为，
故答案为：．
从中随机地抽出一张共有种等可能结果，其中抽出标有数字的纸签的有种结果，再根据概率公式求解即可．
本题主要考查概率公式，随机事件的概率事件可能出现的结果数所有可能出现的结果数．
 

13.【答案】 

【解析】解：，
，，
在和中，
，
≌，
，
，
故答案为：．
由“”可证≌，可得，即可求解．
本题考查了全等三角形的判定和性质，证明三角形全等是解题的关键．
 

14.【答案】解：原式


． 

【解析】根据幂的乘方运算法则将原式化简后，再进行乘法和加法运算．
本题考查了实数的运算，解题关键在于对原式进行合理的化简运算．
 

15.【答案】   

【解析】解：；；
故答案为：；；

若继续不停转动转盘，当很大时，落在“谢谢参与”区域的频率将会接近，晓慧转到“谢谢参与”的概率约是．
根据频率和频数的关系求得和的值即可；
利用大量重复试验中的频率稳定值估计概率即可．
本题考查了利用频率估计概率．大量反复试验下频率稳定值即概率．用到的知识点为：概率所求情况数与总情况数之比．
 

16.【答案】解：原式
，
当时，
原式

． 

【解析】根据完全平方公式、整式的加减运算以及乘法运算进行化简，然后将的值代入原式即可求出答案．
本题考查整式的混合运算，解题的关键是熟练运用完全平方公式、整式的加减运算以及乘法运算，本题属于基础题型．
 

17.【答案】解：如图，点即为所求．
 

【解析】根据要求作出图形即可．
本题考查作图基本作图，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
 

18.【答案】解：圆柱的高是自变量，圆柱的侧面积是因变量；
；
当时，
 

【解析】根据函数的定义，可得答案；
根据圆柱的体积公式，可得答案；
本题考查了函数关系式，利用圆柱的体积公式是解题关键．
 

19.【答案】解：如图所示，即为所求；

如图所示，直线即为所求． 

【解析】根据轴对称变换的性质找出对应点即可求解；
根据对称的性质结合网格即可求解．
本题考查了轴对称变换的性质，熟练掌握轴对称变换的性质是解题的关键．
 

20.【答案】解：是的垂直平分线，
，
，
，，
，
平分，
，
． 

【解析】根据线段的垂直平分线的性质、三角形内角和定理解答即可．
本题考查的是线段的垂直平分线的性质、三角形内角和定理，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
 

21.【答案】解：，
，
，
，
，
，
在和中，
，
≌，
，
，
． 

【解析】根据直角三角形的两锐角互余及平角的定义得出，利用证明≌，根据全等三角形的性质即可得解．
此题考查了全等三角形的判定与性质，熟记全等三角形的判定与性质是解题的关键．
 

22.【答案】解：由题意得，．
板材原来的面积即长方形的面积是．
扩大板材后，长为，宽为．
扩大后的板材面积为．
板材面积增加后比原来多的面积为． 

【解析】根据长方形的面积公式以及多项式乘多项式的乘法法则解决此题．
根据长方形的面积公式以及多项式乘多项式的乘法法则解决此题．
本题主要考查多项式乘多项式，熟练掌握多项式乘多项式的乘法法则是解决本题的关键．
 

23.【答案】   

【解析】解：由图象可得，
学校到实践基地的距离为米，小卖部到实践基地的距离为米，
故答案为：，；
由图象可得，
张敏与同学在实践基地停留了分钟，
他们在小卖部买水用了分钟，
即张敏与同学在实践基地停留了分钟，他们在小卖部买水用了分钟；
分钟小时分钟，
他们上午：从学校出发，
他们：回到学校．
根据函数图象中的数据，可以写出学校到实践基地的距离和小卖部到实践基地的距离；
根据图象中的数据，可以计算出张敏与同学在实践基地停留了多长时间，他们在小卖部买水用了多长时间；
根据图象中的数据，可以计算出他们几点回到学校．
本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．
 

24.【答案】解：，，
，
平分，
；
，
理由：，，
，
，
，
平分，，
，
，
． 

【解析】根据平行线的性质及角平分线的定义求解即可；
根据等腰三角形的性质以及三角形内角和定理可得，由对顶角相等，根据平分得，根据内错角相等，两直线平行即可得出结论．
本题主要考查了等腰三角形的性质，平行线的判定，角平分线的定义的运用，解决问题的关键是掌握等腰三角形的性质以及平行线的判定定理．解题过程中，注意“数形结合”数学思想的运用．
 

25.【答案】     

【解析】解：下列事件中：不可能事件是从袋子摸出球是黑球；
必然事件是从袋子同时摸出个球至少有一个是白球；
随机事件是从袋子同时摸出个球都是红球，
故答案为：、、；

从袋子摸出个球是红球的概率为：；

根据题意，得：，
解得．
根据不可能事件、必然事件及随机事件的概念逐一判断即可；
用红球的数量除以球的总数量即可；
用变化后红球的数量除以球的总数量等于摸到红球的概率列出方程，解之即可．
本题主要考查概率公式，解题的关键是掌握不可能事件、必然事件及随机事件的概念及概率公式．
 

26.【答案】解：≌．
理由：，，
，
，
在和中，
，
≌；
≌，
，
，
，
，
，，
，
，
． 

【解析】首先证明，再利用证明≌；
由全等三角形的性质证出，由平行线的性质和等腰三角形的性质可知，则可得出答案．
本题主要考查了等腰三角形的性质，平行线的性质，全等三角形的判定与性质，证明≌是解题的关键．