八年级下册2 平行四边形的判定图文课件ppt

这是一份八年级下册2 平行四边形的判定图文课件ppt，共27页。PPT课件主要包含了学习目标，这个结论正确吗，平行四边形，平行四边形对角相等，对角线，五种判定方法，平行线间的距离和性质等内容，欢迎下载使用。

1.探索并证明平行四边形其他相关的结论，发展演绎能力； 2.利用平行四边形的判定研究“夹在平行线之间的平行线段相等”，并理解平行线之间的距离； 3.能够综合运用平行四边形的判定定理和性质进行计算和证明．
1.平行四边形的判定对边平行的四边形是平行四边形；对边相等的四边形是平行四边形；对角相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形一组对边平行且相等的四边形是平行四边形
在笔直的铁轨上,夹在铁轨之间的平行枕木是否一样长?你能说明理由吗?
一样长，在铁轨之间的平行枕木之间构成许多平行四边形，平行四边形对边相等
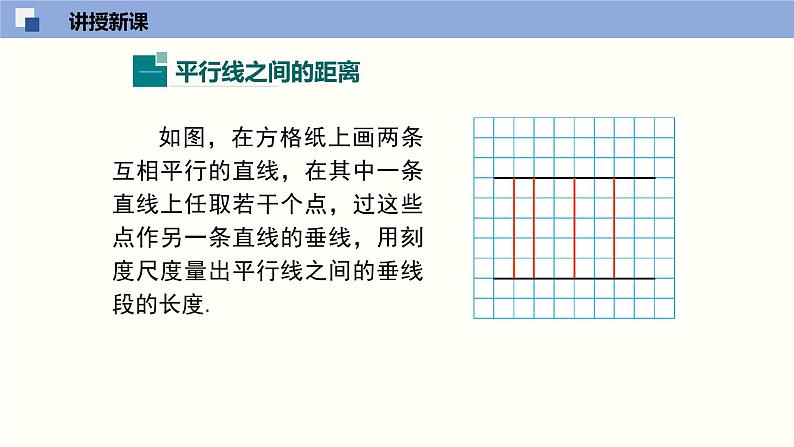
如图，在方格纸上画两条互相平行的直线，在其中一条直线上任取若干个点，过这些点作另一条直线的垂线，用刻度尺度量出平行线之间的垂线段的长度.
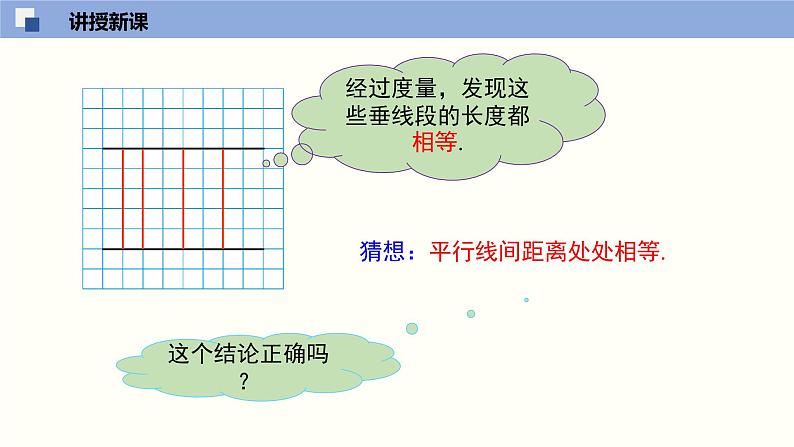
经过度量，发现这些垂线段的长度都相等.
猜想：平行线间距离处处相等.
例: 已知：如图,直线a∥b，A、B是直线a上任意两点，AC⊥b，BD⊥b，垂足分别为C，D.求证：AC＝BD.
证明：∵AC⊥CD，BD⊥CD， ∴∠1＝∠2＝90°. ∴AC∥BD. ∵ AB∥CD. ∴四边形ACDB是平行四边形(平行四边形的定义). ∴AC＝BD(平行四边形的对边相等).
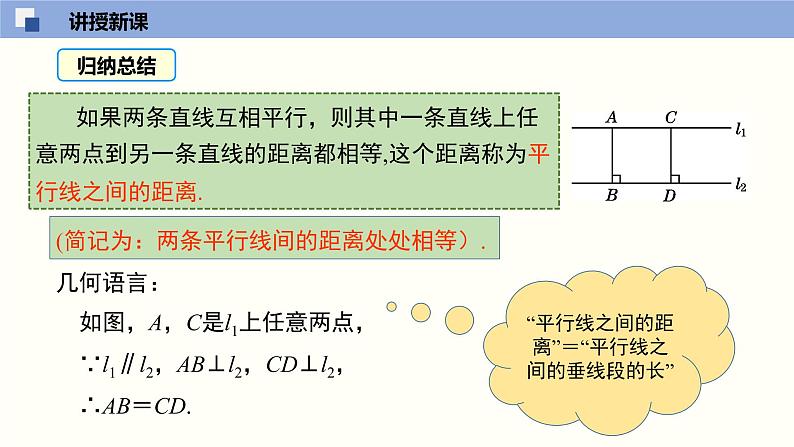
如果两条直线互相平行，则其中一条直线上任意两点到另一条直线的距离都相等,这个距离称为平行线之间的距离.
“平行线之间的距离”＝“平行线之间的垂线段的长”
几何语言：如图，A，C是l1上任意两点，∵l1∥l2，AB⊥l2，CD⊥l2，∴AB＝CD.
(简记为：两条平行线间的距离处处相等）.
若垂线段改为夹在两条平行线间的平行线段呢？它们是否相等呢？
由“两组对边分别平行的四边形是平行四边形”易知其围成的封闭图形为平行四边形，再由平行四边形性质易知夹在两条平行线间的平行线段相等.
如图，已知直线 l∥AB，点 P1，P2，P3都在 l 上，△ABP1，△ABP2，△ABP3 的面积是否相等？为什么．
答：面积相等，同底等高．
(1)夹在两条平行线间的任何平行线段都相等；(2)等(或同)底等（或同）高的三角形的面积相等．
定义： 两组对边分别平行的四边形叫平行四边形
平行四边形对边平行且相等
平行四边形对角线互相平分
两组对边分别相等的四边形
一组对边平行且相等的四边形
对角线互相平分的四边形
两组对边分别平行的四边形
例.已知：如图，在□ABCD中，点M，N分别在AD和BC上，点E，F在BD上，且DM=BN，DF=BE．求证：四边形MENF是平行四边形．
证明：∵ 四边形ABCD是平行四边形，∴ AD∥BC（平行四边形的定义）．∴ ∠MDF=∠NBE．∵ DM=BN，DF=BE，∴ △MDF≌△NBE．
∴ MF=NE，∠MFD=∠NEB．∴ ∠MFE=∠NEF．∴ MF∥NE．∴ 四边形MENF是平行四边形（一组对边平行且相等的四边形是平行四边形）．
例：如图，在 ABCD中，AE⊥BD于E，CF⊥BD于F，连接AF，CE．求证：AF=CE．
证明：∵四边形ABCD是平行四边形
∴AB=CD，AB∥CD，
∴∠ABE=∠CDF．又∵AE⊥BD，CF⊥BD，∴∠AEB=∠CFD=90°，AE∥CF，
在△ABE和△CDF中，∠ABE＝∠CDF， ∠AEB＝∠CFD，AB＝CD ，∴△ABE≌△CDF（AAS）．∴AE=CF，∵AE∥CF，∴四边形AECF是平行四边形，∴AF=CE．
证明：∵四边形ABCD是平行四边形，∴AD=BC，AB//CD，∠FAD=∠ECB.∵AE//CF，∴四边形AECF是平行四边形，∴AF=CE. ∴△FAD≌△ECB(SAS). ∴∠AFD=∠CEB.∵AB//CD，∴∠AFD=∠FDC. ∴∠FDC=∠CEB. ∴DF//BE.又∵AE//CF，∴四边形GEHF是平行四边形.∴EG=FH.
1.如图，已知a∥b，AB∥CD，CE⊥b，FG⊥b，点E，G为垂足，则下列结论中错误的是(　　)A．AB＝CD B．CE＝FGC．A，B两点间的距离就是线段AB的长D．直线a，b间的距离就是线段CD的长
2. 如图，已知直线a∥b，点A，B，C在直线a上，点D，E，F在直线b上，AB＝EF＝2，若△CEF的面积为5，则△ABD的面积为(　　)A．2 B．4 C．5 D．10
3.如图，在平行四边形ABCD中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，给出下列四个条件：①AE=CF；②DE=BF；③∠ADE=∠CBF；④∠ABE=∠CDF．其中不能判定四边形DEBF是平行四边形的有（　　）A．0个 B．1个 C．2个 D．3个
4.如图，以BC为底边的等腰△ABC，点D，E，G分别在BC，AB，AC上，且EG//BC，DE∥AC，延长GE至点F，使得BF=BE.
求证：四边形BDEF为平行四边形；
证明：∵△ABC是等腰三角形，∴∠ABC=∠C.∵EG//BC，DE//AC，∴∠AEG=∠ABC=∠C，四边形CDEG是平行四边形.∴∠DEG=∠C. ∴∠AEG=∠DEG.∵BE=BF，∴∠BFE=∠BEF=∠AEG=∠DEG.∴BF//DE.又∵FG//BC，∴四边形BDEF为平行四边形.
5.如图，将平行四边形ABCD沿CE折叠，使点D落在BC边上的F处.求证：四边形ABFE是平行四边形.
证明：∵将平行四边形ABCD沿CE折叠，使点D落在BC边上的F处，∴EF=ED，∠CFE=∠CDE.∵四边形ABCD是平行四边形∴AD∥BC，∠B=∠D，∴AE∥BF，∠B=∠CFE，∴AB∥EF，∴四边形ABFE是平行四边形.
6.如图，在△ABC中，∠ACB＝90°，∠CAB＝30°，以线段AB为边向外作等边△ABD，点E是线段AB的中点，连接CE并延长交线段AD于点F.
(1)求证：四边形BCFD为平行四边形；
(2)若AB＝6，求平行四边形BCFD的面积．
（1）证明：∵∠ACB＝90°，∠CAB＝30°，∴AB＝2BC，∠ABC＝60°.∵△ABD为等边三角形，∴∠BAD＝∠DBA＝60°，∴∠BAD＝∠ABC＝60°. ∴AD∥BC.∵E为AB的中点，∴AB＝2AE＝2BE，∴BE＝BC，∴△BCE为等边三角形，∴∠BCE＝∠CBE＝60°.∴∠DBC＝∠DBA＋∠CBE＝120°，∴∠DBC＋∠BCE＝180°，∴FC∥BD.∴四边形BCFD是平行四边形．
对边平行,对边相等，对角相等，对角线互相平分
应用：利用等底（或同底）等高（或同高）思考