高中数学湘教版（2019）必修 第一册4.1 实数指数幂和幂函数一等奖教学设计

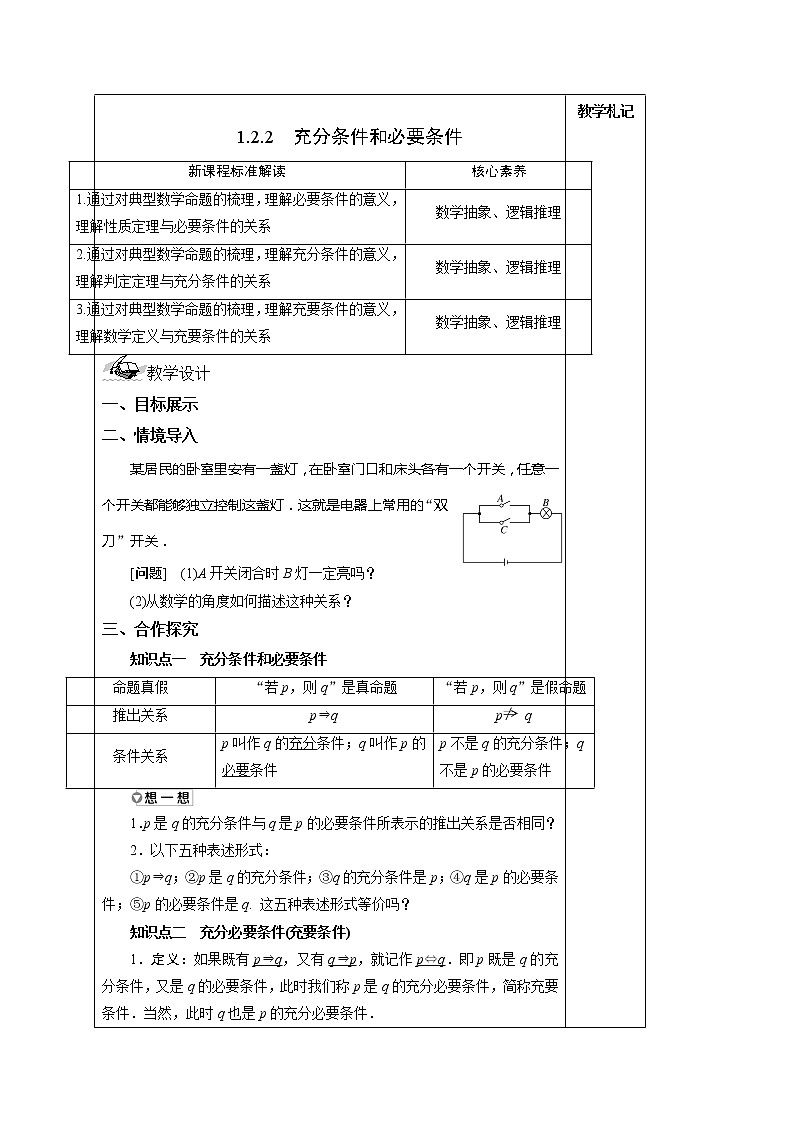
1.2.2　充分条件和必要条件

教学设计

一、目标展示

二、情境导入

某居民的卧室里安有一盏灯，在卧室门口和床头各有一个开关，任意一个开关都能够独立控制这盏灯．这就是电器上常用的“双刀”开关．

[问题]　(1)A开关闭合时B灯一定亮吗？

(2)从数学的角度如何描述这种关系？

三、合作探究

知识点一　充分条件和必要条件

1．p是q的充分条件与q是p的必要条件所表示的推出关系是否相同？

2．以下五种表述形式：

①p⇒q；②p是q的充分条件；③q的充分条件是p；④q是p的必要条件；⑤p的必要条件是q. 这五种表述形式等价吗？

知识点二　充分必要条件(充要条件)

1．定义：如果既有p⇒q，又有q⇒p，就记作p⇔q．即p既是q的充分条件，又是q的必要条件，此时我们称p是q的充分必要条件，简称充要条件．当然，此时q也是p的充分必要条件．

2．记法：如果p是q的充要条件，就记作p⇔q，称为“         ”．

3．传递性：“⇒”和“⇔”都具有传递性，即

(1)如果p⇒q，q⇒s，那么p⇒s；        (2)如果p⇔q，q⇔s，那么p⇔s．

1．若p是q的充要条件，则命题p和q是两个相互等价的命题，这种说法对吗？

2．“p是q的充要条件”与“p的充要条件是q”的区别在哪里？

四、精讲点拨

[例1]　(链接教科书第16页例3)下列各题中，p是q的什么条件？

(1)p：x＝1或x＝2，q：x－1＝；

(2)p：四边形是正方形，q：四边形的对角线互相垂直平分；

(3)p：xy>0，q：x>0，y>0；

(4)p：四边形的对角线相等，q：四边形是平行四边形．

[例2]　已知p：－2≤x≤10，q：1－m≤x≤1＋m(m>0)，若p是q的必要不充分条件，求实数m的取值范围．

[母题探究]

1．(变条件)若本例中“p是q的必要不充分条件”改为“p是q的充分不必要条件”，其他条件不变，求实数m的取值范围．

2．(变设问)本例中p，q不变，是否存在实数m使p是q的充要条件？若存在，求出m的值；若不存在，说明理由．

[例3]　(链接教科书第17页例4)求证：方程x2－2x－3m＝0有两个同号且不相等实根的充要条件是－<m<0.

[例4]　(1)关于x的一元二次方程x2＋x＋m＝0有实数解的一个必要条件是(　　)

A．m<　　　B．m<     C．m<－  D．m<－

(2)若a，b都是实数，试从①ab＝0；②a＋b＝0；③ab>0中分别选出适合下列条件者，用序号填空．(ⅰ)a，b都为0的必要条件是_____；(ⅱ)使a，b都不为0的充分条件是_______．

五、达标检测

1．设x∈R，则“1<x<2”是“1<x<3”的(　　)

A．必要不充分条件　　 B．充分不必要条件

C．充要条件  D．既不充分又不必要条件

2．设a，b是实数，则“a＋b>0”是“ab>0”的(　　)

A．充分不必要条件  B．必要不充分条件

C．充要条件  D．既不充分又不必要条件

3．(多选)设计如图所示的四个电路图，若p：开关S闭合，q：灯泡L亮，则p是q的充要条件的电路图是(　　)

六、课堂小结

1.充分、必要、充要条件的判断；

2.充分条件与必要条件的应用；

3.充要条件的证明；

4.充分条件、必要条件、充要条件的探求.

课后作业

教后反思

教学札记

教学札记