

辽宁省朝阳市三年(2020-2022)中考数学真题分类汇编-03解答题
展开辽宁省朝阳市三年(2020-2022)中考数学真题分类汇编-03解答题
一.分式的化简求值(共3小题)
1.(2022•朝阳)先化简,简求值:÷+,其中x=()﹣2.
2.(2021•朝阳)先化简,再求值:(+1)÷,其中x=tan60°.
3.(2020•朝阳)先化简,再求值:,其中.
二.一元二次方程的应用(共1小题)
4.(2021•朝阳)某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于38元,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间符合一次函数关系,如图所示.
(1)求y与x之间的函数关系式;
(2)该商场销售这种商品要想每天获得600元的利润,每件商品的售价应定为多少元?
(3)设商场销售这种商品每天获利w(元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润是多少?
三.分式方程的应用(共1小题)
5.(2021•朝阳)为了进一步丰富校园文体活动,学校准备购进一批篮球和足球,已知每个篮球的进价比每个足球的进价多25元,用2000元购进篮球的数量是用750元购进足球数量的2倍,求:每个篮球和足球的进价各多少元?
四.一元一次不等式的应用(共1小题)
6.(2022•朝阳)某中学要为体育社团购买一些篮球和排球,若购买3个篮球和2个排球,共需560元;若购买2个篮球和4个排球,共需640元.
(1)求每个篮球和每个排球的价格分别是多少元;
(2)该中学决定购买篮球和排球共10个,总费用不超过1100元,那么最多可以购买多少个篮球?
五.二次函数的应用(共2小题)
7.(2022•朝阳)某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?
(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
8.(2020•朝阳)某公司销售一种商品,成本为每件30元,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的三组对应数值如下表:
销售单价x(元)
40
60
80
日销售量y(件)
80
60
40
(1)直接写出y与x的关系式 ;
(2)求公司销售该商品获得的最大日利润;
(3)销售一段时间以后,由于某种原因,该商品每件成本增加了10元,若物价部门规定该商品销售单价不能超过a元,在日销售量y(件)与销售单价x(元)保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求a的值.
六.二次函数综合题(共3小题)
9.(2022•朝阳)如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)求抛物线的解析式及点B的坐标.
(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.
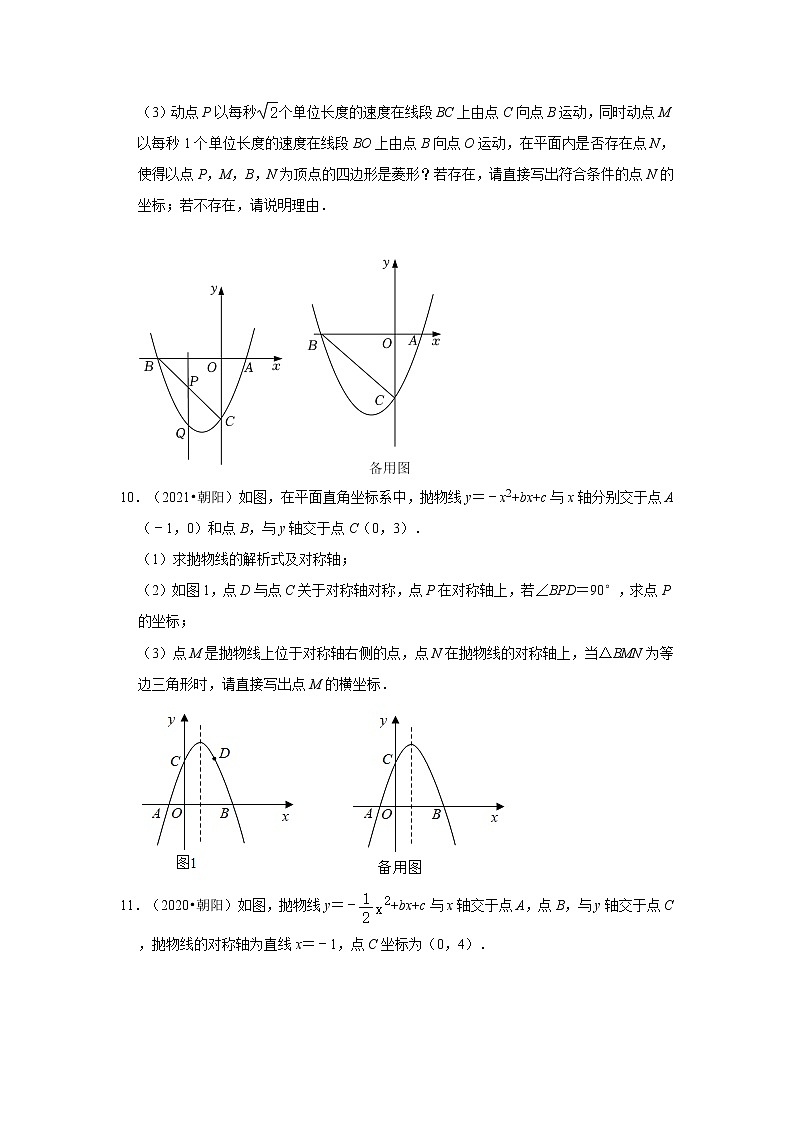
(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.
10.(2021•朝阳)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)和点B,与y轴交于点C(0,3).
(1)求抛物线的解析式及对称轴;
(2)如图1,点D与点C关于对称轴对称,点P在对称轴上,若∠BPD=90°,求点P的坐标;
(3)点M是抛物线上位于对称轴右侧的点,点N在抛物线的对称轴上,当△BMN为等边三角形时,请直接写出点M的横坐标.
11.(2020•朝阳)如图,抛物线y=﹣+bx+c与x轴交于点A,点B,与y轴交于点C,抛物线的对称轴为直线x=﹣1,点C坐标为(0,4).
(1)求抛物线表达式;
(2)在抛物线上是否存在点P,使∠ABP=∠BCO,如果存在,求出点P坐标;如果不存在,请说明理由;
(3)在(2)的条件下,若点P在x轴上方,点M是直线BP上方抛物线上的一个动点,求点M到直线BP的最大距离;
(4)点G是线段AC上的动点,点H是线段BC上的动点,点Q是线段AB上的动点,三个动点都不与点A,B,C重合,连接GH,GQ,HQ,得到△GHQ,直接写出△GHQ周长的最小值.
七.四边形综合题(共2小题)
12.(2022•朝阳)【思维探究】
(1)如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.
小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明△ADE≌△ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.
【思维延伸】
(2)如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.
【思维拓展】
(3)在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=,AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.
13.(2020•朝阳)如图,在Rt△ABC中,∠BAC=90°,AB=AC,M是AC边上的一点,连接BM,作AP⊥BM于点P,过点C作AC的垂线交AP的延长线于点E.
(1)如图1,求证:AM=CE;
(2)如图2,以AM,BM为邻边作平行四边形AMBG,连接GE交BC于点N,连接AN,求的值;
(3)如图3,若M是AC的中点,以AB,BM为邻边作平行四边形AGMB,连接GE交BC于点N,连接AN,经探究发现,请直接写出的值.
八.切线的判定与性质(共1小题)
14.(2021•朝阳)如图,AB是⊙O的直径,点D在⊙O上,且∠AOD=90°,点C是⊙O外一点,分别连接CA,CB、CD,CA交⊙O于点M,交OD于点N,CB的延长线交⊙O于点E,连接AD,ME,且∠ACD=∠E.
(1)求证:CD是⊙O的切线;
(2)连接DM,若⊙O的半径为6,tanE=,求DM的长.
九.几何变换综合题(共1小题)
15.(2021•朝阳)如图,在Rt△ABC中,AC=BC,∠ACB=90°,点O在线段AB上(点O不与点A,B重合),且OB=kOA,点M是AC延长线上的一点,作射线OM,将射线OM绕点O逆时针旋转90°,交射线CB于点N.
(1)如图1,当k=1时,判断线段OM与ON的数量关系,并说明理由;
(2)如图2,当k>1时,判断线段OM与ON的数量关系(用含k的式子表示),并证明;
(3)点P在射线BC上,若∠BON=15°,PN=kAM(k≠1),且<,请直接写出的值(用含
k的式子表示).
一十.相似三角形的判定与性质(共2小题)
16.(2022•朝阳)如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
(1)求证:AF是⊙O的切线;
(2)若⊙O的半径为5,AD是△AEF的中线,且AD=6,求AE的长.
17.(2020•朝阳)如图,以AB为直径的⊙O经过△ABC的顶点C,过点O作OD∥BC交⊙O于点D,交AC于点F,连接BD交AC于点G,连接CD,在OD的延长线上取一点E,连接CE,使∠DEC=∠BDC.
(1)求证:EC是⊙O的切线;
(2)若⊙O的半径是3,DG•DB=9,求CE的长.
一十一.作图-位似变换(共1小题)
18.(2020•朝阳)如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图:
(1)以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1,请画出△A1B1C1;
(2)以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2,使它与△ABC的位似比为2:1.
一十二.解直角三角形的应用-仰角俯角问题(共2小题)
19.(2022•朝阳)某数学兴趣小组准备测量校园内旗杆顶端到地面的高度(旗杆底端有台阶).该小组在C处安置测角仪CD,测得旗杆顶端A的仰角为30°,前进8m到达E处,安置测角仪EF,测得旗杆顶端A的仰角为45°(点B,E,C在同一直线上),测角仪支架高CD=EF=1.2m,求旗杆顶端A到地面的距离即AB的长度.(结果精确到1m.参考数据:≈1.7)
20.(2021•朝阳)一数学兴趣小组去测量一棵周围有围栏保护的古树的高,在G处放置一个小平面镜,当一位同学站在F点时,恰好在小平面镜内看到这棵古树的顶端A的像,此时测得FG=3m,这位同学向古树方向前进了9m后到达点D,在D处安置一高度为1m的测角仪CD,此时测得树顶A的仰角为30°,已知这位同学的眼睛与地面的距离EF=1.5m,点B,D,G,F在同一水平直线上,且AB,CD,EF均垂直于BF,求这棵古树AB的高.(小平面镜的大小和厚度忽略不计,结果保留根号)
一十三.解直角三角形的应用-方向角问题(共1小题)
21.(2020•朝阳)为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是30km/h,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由(结果保留根号).
一十四.用样本估计总体(共1小题)
22.(2022•朝阳)为了解学生的睡眠情况,某校随机抽取部分学生对他们最近两周的睡眠情况进行调查,得到他们每日平均睡眠时长x(单位:h)的一组数据,将所得数据分为四组(A:x<8;B:8≤x<9;C:9≤x<10;D:x≥10),并绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)本次一共抽样调查了 名学生.
(2)求出扇形统计图中D组所对应的扇形圆心角的度数.
(3)将条形统计图补充完整.
(4)若该校共有1200名学生,请估计最近两周有多少名学生的每日平均睡眠时长大于或等于9h.
一十五.条形统计图(共2小题)
23.(2021•朝阳)“赏中华诗词,寻文化基因,品文学之美”,某校对全体学生进行了古诗词知识测试,将成绩分为一般、良好、优秀三个等级,从中随机抽取部分学生的测试成绩,根据调查结果绘制成两幅不完整的统计图,根据图中信息,解答下列问题:
(1)求本次抽样调查的人数;
(2)在扇形统计图中,阴影部分对应的扇形圆心角的度数是 ;
(3)将条形统计图补充完整;
(4)该校共有1500名学生,根据抽样调查的结果,请你估计测试成绩达到优秀的学生人数.
24.(2020•朝阳)由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如图两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)在扇形统计图中,m的值是 ,D对应的扇形圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式D的学生人数.
一十六.列表法与树状图法(共3小题)
25.(2022•朝阳)某社区组织A,B,C,D四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.
(1)王明被安排到A小区进行服务的概率是 .
(2)请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.
26.(2021•朝阳)为了迎接建党100周年,学校举办了“感党恩•跟党走”主题社团活动,小颖喜欢的社团有写作社团、书画社团、演讲社团、舞蹈社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片正面,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小颖从中随机抽取一张卡片是舞蹈社团D的概率是 ;
(2)小颖先从中随机抽取一张卡片,记录下卡片上的字母不放回,再从剩下的卡片中随机抽取一张卡片,记录下卡片上的字母,请用列表法或画树状图法求出小颖抽取的两张卡片中有一张是演讲社团C的概率.
27.(2020•朝阳)某校准备组建“校园安全宣传队”,每班有两个队员名额,七年2班有甲、乙、丙、丁四位同学报名,这四位同学综合素质都很好,王老师决定采取抽签的方式确定人选.具体做法是:将甲、乙、丙、丁四名同学分别编号为1、2、3、4号,将号码分别写在4个大小、质地、形状、颜色均无差别的小球上,然后把小球放入不透明的袋子中,充分搅拌均匀后,王老师从袋中随机摸出两个小球,根据小球上的编号确定本班“校园安全宣传员”人选.
(1)用画树状图或列表法,写出“王老师从袋中随机摸出两个小球”可能出现的所有结果.
(2)求甲同学被选中的概率.
辽宁省朝阳市三年(2020-2022)中考数学真题分类汇编-03解答题
参考答案与试题解析
一.分式的化简求值(共3小题)
1.(2022•朝阳)先化简,简求值:÷+,其中x=()﹣2.
【分析】把除化为乘,再算同分母的分式相加,化简后求出x的值,代入即可.
【解答】解:原式=•+
=+
=
=
=x,
∵x=()﹣2=4,
∴原式=4.
2.(2021•朝阳)先化简,再求值:(+1)÷,其中x=tan60°.
【分析】先把括号内的分式通分,再把各分子和分母因式分解,然后进行约分化简,代入求值即可.
【解答】解:原式=÷
=×
=.
x=tan60°=,代入得:原式==1+.
3.(2020•朝阳)先化简,再求值:,其中.
【分析】根据分式的加法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
【解答】解:
=
=
=,
当时,原式=.
二.一元二次方程的应用(共1小题)
4.(2021•朝阳)某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于38元,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间符合一次函数关系,如图所示.
(1)求y与x之间的函数关系式;
(2)该商场销售这种商品要想每天获得600元的利润,每件商品的售价应定为多少元?
(3)设商场销售这种商品每天获利w(元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润是多少?
【分析】(1)利用待定系数法求解即可;
(2)根据“每件利润×销售量=总利润”列出一元二次方程,解之可得;
(3)根据以上相等关系列出函数解析式,配方成顶点式,利用二次函数性质求解可得.
【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
由所给函数图象可知:,
解得,
故y与x的函数关系式为y=﹣2x+120;
(2)根据题意,得:(x﹣20)(﹣2x+120)=600,
整理,得:x2﹣80x+1500=0,
解得:x=30或x=50(不合题意,舍去),
答:每件商品的销售价应定为30元;
(3)∵y=﹣2x+120,
∴w=(x﹣20)y=(x﹣20)(﹣2x+120)
=﹣2x2+160x﹣2400
=﹣2(x﹣40)2+800,
∵x≤38
∴当x=38时,w最大=792,
∴售价定为38元/件时,每天最大利润w=792元.
三.分式方程的应用(共1小题)
5.(2021•朝阳)为了进一步丰富校园文体活动,学校准备购进一批篮球和足球,已知每个篮球的进价比每个足球的进价多25元,用2000元购进篮球的数量是用750元购进足球数量的2倍,求:每个篮球和足球的进价各多少元?
【分析】设每个足球的进价是x元,则每个篮球的进价是(x+25)元,利用数量=总价÷单价,结合用2000元购进篮球的数量是用750元购进足球数量的2倍,即可得出关于x的分式方程,解之经检验后即可得出足球的单价,再将其代入(x+25)中即可求出篮球的单价.
【解答】解:设每个足球的进价是x元,则每个篮球的进价是(x+25)元,
依题意得:=2×,
解得:x=75,
经检验,x=75是原方程的解,且符合题意,
∴x+25=75+25=100.
答:每个足球的进价是75元,每个篮球的进价是100元.
四.一元一次不等式的应用(共1小题)
6.(2022•朝阳)某中学要为体育社团购买一些篮球和排球,若购买3个篮球和2个排球,共需560元;若购买2个篮球和4个排球,共需640元.
(1)求每个篮球和每个排球的价格分别是多少元;
(2)该中学决定购买篮球和排球共10个,总费用不超过1100元,那么最多可以购买多少个篮球?
【分析】(1)设每个篮球的价格是x元,每个排球的价格是y元,可得:,即可解得每个篮球的价格是120元,每个排球的价格是100元;
(2)设购买m个篮球,可得:120m+100(10﹣m)≤1100,即可解得最多可以购买5个篮球.
【解答】解:(1)设每个篮球的价格是x元,每个排球的价格是y元,
根据题意得:,
解得,
∴每个篮球的价格是120元,每个排球的价格是100元;
(2)设购买m个篮球,
根据题意得:120m+100(10﹣m)≤1100,
解得m≤5,
答:最多可以购买5个篮球.
五.二次函数的应用(共2小题)
7.(2022•朝阳)某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?
(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
【分析】(1)根据给定的数据,利用待定系数法即可求出y与x之间的函数关系式;
(2)根据每件的销售利润×每天的销售量=425,解一元二次方程即可;
(3)利用销售该消毒用品每天的销售利润=每件的销售利润×每天的销售量,即可得出w关于x的函数关系式,再利用二次函数的性质即可解决最值问题.
【解答】解:(1)设每天的销售量y(件)与每件售价x(元)函数关系式为:y=kx+b,
由题意可知:,
解得:,
∴y与x之间的函数关系式为:y=﹣5x+150;
(2)(﹣5x+150)(x﹣8)=425,
解得:x1=13,x2=25(舍去),
∴若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为13元;
(3)w=y(x﹣8),
=(﹣5x+150)(x﹣8),
w=﹣5x2+190x﹣1200,
=﹣5(x﹣19)2+605,
∵8≤x≤15,且x为整数,
当x<19时,w随x的增大而增大,
∴当x=15时,w有最大值,最大值为525.
答:每件消毒用品的售价为15元时,每天的销售利润最大,最大利润是525元.
8.(2020•朝阳)某公司销售一种商品,成本为每件30元,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的三组对应数值如下表:
销售单价x(元)
40
60
80
日销售量y(件)
80
60
40
(1)直接写出y与x的关系式 y=﹣x+120 ;
(2)求公司销售该商品获得的最大日利润;
(3)销售一段时间以后,由于某种原因,该商品每件成本增加了10元,若物价部门规定该商品销售单价不能超过a元,在日销售量y(件)与销售单价x(元)保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求a的值.
【分析】(1)根据题中所给的表格中的数据,利用待定系数法可得其关系式,也可以根据关系直接写出关系式;
(2)根据利润等于每件的利润乘以件数,再利用配方法求得其最值;
(3)根据题意,列出关系式,再分类讨论求最值,比较得到结果.
【解答】解:(1)设解析式为y=kx+b,
将(40,80)和(60,60)代入,可得,解得:,
所以y与x的关系式为y=﹣x+120,
故答案为:y=﹣x+120;
(2)设公司销售该商品获得的日利润为w元,
w=(x﹣30)y=(x﹣30)(﹣x+120)=﹣x2+150x﹣3600=﹣(x﹣75)2+2025,
∵x﹣30≥0,﹣x+120≥0,
∴30≤x≤120,
∵﹣1<0,
∴抛物线开口向下,函数有最大值,
∴当x=75时,w最大=2025,
答:当销售单价是75元时,最大日利润是2025元.
(3)w=(x﹣30﹣10)(﹣x+120)=﹣x2+160x﹣4800=﹣(x﹣80)2+1600,
当w最大=1500时,﹣(x﹣80)2+1600=1500,
解得x1=70,x2=90,
∵40≤x≤a,
∴有两种情况,
①a<80时,在对称轴左侧,w随x的增大而增大,
∴当x=a=70时,w最大=1500,
②a≥80时,在40≤x≤a范围内w最大=1600≠1500,
∴这种情况不成立,
∴a=70.
六.二次函数综合题(共3小题)
9.(2022•朝阳)如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)求抛物线的解析式及点B的坐标.
(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.
(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.
【分析】(1)将A,C两点坐标代入抛物线的解析式求得a,c的值,进而得出解析式,当y=0时,求出方程的解,进而求得B点坐标;
(2)由B,C两点求出BC的解析式,进而设出点P和点Q坐标,表示出PQ的长,进一步得出结果;
(3)要使以点P,M,B,N为顶点的四边形是菱形,只需△PMB是等腰三角形,所以分为PM=BM,PM=PB和BP=BM,结合图象,进一步得出结果.
【解答】解:(1)由题意得,
,
∴,
∴y=x2+2x﹣3,
当y=0时,x2+2x﹣3=0,
∴x1=1,x2=﹣3,
∴B(﹣3,0);
(2)设直线BC的解析式为:y=kx+b,
∴,
∴,
∴y=﹣x﹣3,
设点P(m,﹣m+3),Q(m,m2+2m﹣3),
∴PQ=(﹣m﹣3)﹣(m2+2m﹣3)=﹣m2﹣3m=﹣(m+)2+,
∴当m=﹣时,PQ最大=;
(3)如图1,
∵B(﹣3,0),C(0,﹣3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°,
作PD⊥y轴于D,
∴CD=PD=PC•sin∠OCB==t,
当BM=PM时,
∴∠MPB=∠OBC=45°,
∵∠PMO=∠PDO=∠MOD=90°,
∴四边形OMPD时矩形,
∴OM=PD=t,
由BM+OM=OB得,
∴2t=3,
∴t=,
∴P(﹣,﹣),
∴N(﹣3,﹣),
如图2,
当PM=PB时,作PD⊥y轴于D,作PE⊥x轴于E,
∴BM=2BE,
可得四边形PDOE是矩形,
∴OE=PD=t,
∴BE=3﹣t,
∴t=2(3﹣t),
∴t=2,
∴P(﹣2,﹣1),
∴N(﹣2,1),
如图3,
当PB=MB时,
3﹣=t,
∴t=6﹣3,
∴P(3,3﹣3),
∴N(0,3﹣3),
综上所述:N(﹣3,﹣)或(﹣2,1)或(0,3﹣3).
10.(2021•朝阳)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)和点B,与y轴交于点C(0,3).
(1)求抛物线的解析式及对称轴;
(2)如图1,点D与点C关于对称轴对称,点P在对称轴上,若∠BPD=90°,求点P的坐标;
(3)点M是抛物线上位于对称轴右侧的点,点N在抛物线的对称轴上,当△BMN为等边三角形时,请直接写出点M的横坐标.
【分析】(1)利用待定系数法求解即可.
(2)如图1中,连接BD,设BD的中点T,连接PT,设P(1,m).求出PT的长,构建方程求出m即可.
(3)分两种情形:当点M在第一象限时,△BMN是等边三角形,过点B作BT⊥BN交NM的延长线于T,设N(1,t),设抛物线的对称轴交x轴于E.如图3﹣2中,当点M在第四象限时,设N(1,n),过点B作BT⊥BN交NM的延长线于T.分别利用相似三角形的性质求出点M的坐标,再利用待定系数法求解.
【解答】解:(1)把A(﹣1,0),点C(0,3)的坐标代入y=﹣x2+bx+c,得到,
解得,
∴抛物线的解析式为y=﹣x2+2x+3,对称轴x=﹣=1.
(2)如图1中,连接BD,设BD的中点T,连接PT,设P(1,m).
∵点D与点C关于对称轴对称,C(0,3),
∴D(2,3),
∵B(3,0),
∴T(,),BD==,
∵∠BPD=90°,DT=TB,
∴PT=BD=,
∴(1﹣)2+(m﹣)2=()2,
解得m=1或2,
∴P(1,1)或(1,2).
(3)当点M在第一象限时,△BMN是等边三角形,过点B作BT⊥BN交NM的延长线于T,设N(1,t),设抛物线的对称轴交x轴于E.
∵△BMN是等边三角形,
∴∠NMB=∠NBM=60°,
∵∠NBT=90°,
∴∠MBT=30°,BT=BN,
∵∠NMB=∠MBT+∠BTM=60°,
∴∠MBT=∠BTM=30°,
∴MB=MT=MN,
∵∠NBE+∠TBJ=90°,∠TBJ+∠BTJ=90°,
∴∠NBE=∠BTJ,
∵∠BEN=∠TJB=90°,
∴△BEN∽△TJB,
∴===,
∴BJ=t,TJ=2,
∴T(3+t,2),
∵NM=MT,
∴M(,),
∵点M在y=﹣x2+2x+3上,
∴=﹣()2+2×+3,
整理得,3t2+(4+2)t﹣12+4=0,
解得t=﹣2(舍弃)或,
∴M(,).
如图3﹣2中,当点M在第四象限时,设N(1,n),过点B作BT⊥BN交NM的延长线于T.
同法可得T(3﹣n,﹣2),M(,),
则有=﹣()2+2×+3,
整理得,3n2+(2﹣4)n﹣12﹣4=0,
解得n=或2(舍弃),
∴M(,),
解法二:连接MA,证明∠MAB=30°,求出直线AM的解析式,构建方程组确定点M的坐标即可.
综上所述,满足条件的点M的横坐标为或.
11.(2020•朝阳)如图,抛物线y=﹣+bx+c与x轴交于点A,点B,与y轴交于点C,抛物线的对称轴为直线x=﹣1,点C坐标为(0,4).
(1)求抛物线表达式;
(2)在抛物线上是否存在点P,使∠ABP=∠BCO,如果存在,求出点P坐标;如果不存在,请说明理由;
(3)在(2)的条件下,若点P在x轴上方,点M是直线BP上方抛物线上的一个动点,求点M到直线BP的最大距离;
(4)点G是线段AC上的动点,点H是线段BC上的动点,点Q是线段AB上的动点,三个动点都不与点A,B,C重合,连接GH,GQ,HQ,得到△GHQ,直接写出△GHQ周长的最小值.
【分析】(1)利用抛物线的对称轴为x=﹣1,求出b的值,再把b的值和C的坐标代入y=﹣+bx+c计算即可;
(2)作PE⊥x轴于点E,利用相似三角形的判定方法可证得△PEB∽△BOC,设,则|,BE=2﹣m,再分别讨论P的位置列式求解即可;
(3)作MF⊥x轴于点F,交BP于点R,作MN⊥BP于点N,用待定系数法求出直线BP的解析式,利用解析式表示出MR的长度,再通过求证△MNR∽△BFR联合Rt△MNR建立比值关系列式计算即可;
(4)作Q点关于AC的对称点Q1,作Q关于CB的对称点Q2,连接Q1Q2与AC于G1,与CB交于点H1,连接QQ1交AC于J,连接QQ2交CB于K,此时△QG1H1的周长最小,这个最小值=Q1Q2,再证明Q1Q2=2JK,JK最小时,△QGH周长最小,利用图2证明当点Q与点O重合时JK最小,在图3中利用相似三角形的性质求出JK的最小值即可解决问题.
【解答】解:(1)∵抛物线对称轴为x=﹣1,
∴﹣=﹣1,
∴b=﹣1,
将(0,4)代入y=﹣﹣x+c中,
∴c=4,
∴y=﹣﹣x+4.
(2)如图1中,作PE⊥x轴于点E.
∵∠ABP=∠BCO,∠PEB=∠BOC=90°,
∴△PEB∽△BOC,
∴(此处也可以由等角的正切值相等得到),
设,则PE=|﹣m2﹣m+4|,BE=2﹣m,
①当点P在x轴上方时:,
解得m1=﹣3,m2=2(不符题意,舍),
②当点P在x轴下方时:,
解得m1=﹣5,m2=2(不符题意,舍),
∴或.
(3)作MF⊥x轴于点F,交BP于点R,作MN⊥BP于点N.
∵y=﹣(x+4)(x﹣2),
∴A(﹣4,0),B(2,0),
设yBP=kx+b1,
将代入得解得k=﹣=1,
∴yBP=﹣x+1,
设,则,
∴a+3,
∵∠MNR=∠RFB=90°,∠NRM=∠FRB,
∴△MNR∽△BFR,
∴,
∵tan∠ABP=,
在Rt△MNR中NR:MN:MR=1:2:,
∴,
∴MN=﹣,
当a=﹣时,MN最大为.
(4)作Q点关于AC的对称点Q1,作Q关于CB的对称点Q2,连接Q1Q2与AC于G1,与CB交于点H1,连接QQ1交AC于J,连接QQ2交CB于K,此时△QG1H1的周长最小,这个最小值=Q1Q2.
∵QJ=JQ1,QK=KQ2,
∴Q1Q2=2JK,
∴当JK最小时,Q1Q2最小,如图2中:
∵∠CJQ=∠CKQ=90°,
∴C、J、Q、K四点共圆,线段CQ就是圆的直径,JK是弦,
∵∠JCK是定值,
∴直径CQ最小时,弦JK最小,
∴当点Q与点O重合时,CQ最小,此时JK最小,如图3中:
∵在Rt△COA中,∠COA=90°,CO=4,AO=4,
∴AC=,
∵Rt△COB,∠COB=90°,CB=,
∵OJ⊥AC,OK⊥CB,
∴OC•OB,
∴OK=,
∴CK=,
∵∠JCO=∠OCA,∠CJO=∠COA,
∴△CJO∽△COA,
∴,
∴CO2=CJ•CA,同理可得:CO2=CK•CB,
∴CJ•CA=CK•CB,
∴,
∵∠JCK=∠BCA,
∴△CJK∽△CBA,
∴=,
∴,
∴JK=,
∴△QGH周长的最小值=Q1Q2=2JK=.
七.四边形综合题(共2小题)
12.(2022•朝阳)【思维探究】
(1)如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.
小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明△ADE≌△ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.
【思维延伸】
(2)如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.
【思维拓展】
(3)在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=,AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.
【分析】(1)如图1中,延长CD到点E,使DE=BC,连接AE.证明△ADE≌△ABC(SAS),推出∠DAE=∠BAC,AE=AC,推出△ACE的等边三角形,可得结论;
(2)结论:CB+CD=AC.如图2中,过点A作AM⊥CD于点M,AN⊥CB交CB的延长线于点N.证明△AMD≌△ANB(AAS),推出DM=BN,AM=AN,证明Rt△ACM≌Rt△ACN(HL),推出CM=CN,可得结论;
(3)分两种情形:如图3﹣1中,当∠CDA=75°时,过点O作OP⊥CB于点P,CQ⊥CD于点Q.如图3﹣2中,当∠CBD=75°时,分别求解即可.
【解答】(1)证明:如图1中,延长CD到点E,使DE=BC,连接AE.
∵∠BAD+∠BCD=180°,
∴∠B+∠ADC=180°,
∵∠ADE+∠ADC=180°
∴∠B=∠ADE,
在△ADE和△ABC中,
,
∴△ADE≌△ABC(SAS),
∴∠DAE=∠BAC,AE=AC,
∴∠CAE=∠BAD=60°,
∴△ACE的等边三角形,
∴CE=AC,
∵CE=DE+CD,
∴AC=BC+CD;
(2)解:结论:CB+CD=AC.
理由:如图2中,过点A作AM⊥CD于点M,AN⊥CB交CB的延长线于点N.
∵∠DAB=∠DCB=90°,
∴∠CDA+∠CBA=180°,
∵∠ABN+∠ABC=180°,
∴∠D=∠ABN,
∵∠AMD=∠N=90°,AD=AB,
∴△AMD≌△ANB(AAS),
∴DM=BN,AM=AN,
∵AM⊥CD,AN⊥CN,
∴∠ACD=∠ACB=45°,
∴AC=CM,
∵AC=AC.AM=AN,
∴Rt△ACM≌Rt△ACN(HL),
∴CM=CN,
∴CB+CD=CN﹣BN+CM+DM=2CM=AC;
(3)解:如图3﹣1中,当∠CDA=75°时,过点O作OP⊥CB于点P,CQ⊥CD于点Q.
∵∠CDA=75°,∠ADB=45°,
∴∠CDB=30°,
∵∠DCB=90°,
∴CD=CB,
∵∠DCO=∠BCO=45°,OP⊥CB,OQ⊥CD,
∴OP=OQ,
∴==,
∴==,
∵AB=AD=,∠DAB=90°,
∴BD=AD=2,
∴OD=×2=3﹣3.
如图3﹣2中,当∠CBD=75°时,同法可证=,OD=×2=3﹣,
综上所述,满足条件的OD的长为3﹣3或3﹣.
13.(2020•朝阳)如图,在Rt△ABC中,∠BAC=90°,AB=AC,M是AC边上的一点,连接BM,作AP⊥BM于点P,过点C作AC的垂线交AP的延长线于点E.
(1)如图1,求证:AM=CE;
(2)如图2,以AM,BM为邻边作平行四边形AMBG,连接GE交BC于点N,连接AN,求的值;
(3)如图3,若M是AC的中点,以AB,BM为邻边作平行四边形AGMB,连接GE交BC于点N,连接AN,经探究发现,请直接写出的值.
【分析】(1)通过证△ABM与△CAE全等可以证得AM=CE;
(2)过点E作EF⊥CE交BC于F,通过证明△ABG与△ACE全等,证得AG=AE,通过△GBN≌△EFN证得GN=EN,最后由直角三角形的性质证得结论;
(3)延长GM交BC于点F,连接AF,在Rt△AFC中,由勾股定理求出AN的长,在Rt△AEG中,求出EG的长即可得到答案.
【解答】(1)证明:∵AP⊥BM,
∴∠APB=90°,
∴∠ABP+∠BAP=90°,
∵∠BAP+∠CAE=90°,
∴∠CAE=∠ABP,
∵CE⊥AC,
∴∠BAM=∠ACE=90°,
∵AB=AC,
∴△ABM≌△CAE(ASA),
∴CE=AM;
(2)过点E作CE的垂线交BC于点F,
∴∠FEC=90°,
∵AB=AC,∠BAC=90°,
∴∠ACB=∠ABC=45°,
∵∠ACE=90°,
∴∠FCE=45°,
∴∠CFE=∠FCE=45°,
∴CE=EF,∠EFN=135°,
∵四边形AMBG是平行四边形,
∴AM=BG,∠ABG=∠BAC=90°,
∴∠GBN=∠ABG+∠ABC=135°,
∴∠GBN=∠EFN,
由(1)得△ABM≌△CAE,
∴AM=CE,
∴BG=CE=EF,
∵∠BNG=∠FNE,
∴△GBN≌△EFN(AAS),
∴GN=EN,
∵AG∥BM,
∴∠GAE=∠BPE=90°,
∴,
∴;
(3)如图,延长GM交BC于F,连接AF,
在平行四边形ABMG中,AB∥GM,△ABM≌△MGA,
∴∠AMG=∠BAC=90°,
∴∠GMC=∠ACE=90°,
∴GF∥CE,
∵AM=MC,
∴BF=CF,
∵AB=AC,
∴,
∵,
设CN=x,则BC=8x,AF=FC=4x,FN=3x,
∴,
在Rt△ABM中,
,,
∴,
∴,
由(1)知△ABM≌△CAE,
∴△CAE≌△MGA,
∴AE=AG,
在Rt△AEG中,EG=,
∴.
八.切线的判定与性质(共1小题)
14.(2021•朝阳)如图,AB是⊙O的直径,点D在⊙O上,且∠AOD=90°,点C是⊙O外一点,分别连接CA,CB、CD,CA交⊙O于点M,交OD于点N,CB的延长线交⊙O于点E,连接AD,ME,且∠ACD=∠E.
(1)求证:CD是⊙O的切线;
(2)连接DM,若⊙O的半径为6,tanE=,求DM的长.
【分析】(1)根据圆周角定理和等量代换可得∠BAC=∠ACD,进而得出AB∥CD,由∠AOD=90°可得OD⊥CD,从得出结论;
(2)由tanE=,可得tan∠ACD=tan∠OAN=tanE=,在直角三角形中由锐角三角函数可求出ON、DN、CD,由勾股定理求出CN,由三角形的面积公式求出DF,再根据圆周角定理可求出∠AMD=45°,进而根据等腰直角三角形的边角关系求出DM即可.
【解答】解:(1)∵∠ACD=∠E,∠E=∠BAC,
∴∠BAC=∠ACD,
∴AB∥CD,
∴∠ODC=∠AOD=90°,
即OD⊥CD,
∴CD是⊙O的切线;
(2)过点D作DF⊥AC于F,
∵⊙O的半径为6,tanE==tan∠ACD=tan∠OAN,
∴ON=OA=×6=2,
∴DN=OD﹣ON=6﹣2=4,
∴CD=3DN=12,
在Rt△CDN中,
CN===4,
由三角形的面积公式可得,
CN•DF=DN•CD,
即4DF=4×12,
∴DF=,
又∵∠AMD=∠AOD=×90°=45°,
在Rt△DFM中,
DM=DF=×=.
九.几何变换综合题(共1小题)
15.(2021•朝阳)如图,在Rt△ABC中,AC=BC,∠ACB=90°,点O在线段AB上(点O不与点A,B重合),且OB=kOA,点M是AC延长线上的一点,作射线OM,将射线OM绕点O逆时针旋转90°,交射线CB于点N.
(1)如图1,当k=1时,判断线段OM与ON的数量关系,并说明理由;
(2)如图2,当k>1时,判断线段OM与ON的数量关系(用含k的式子表示),并证明;
(3)点P在射线BC上,若∠BON=15°,PN=kAM(k≠1),且<,请直接写出的值(用含
k的式子表示).
【分析】(1)作OD⊥AM,OE⊥BC,证明△DOM≌△EON;
(2)作OD⊥AM,OE⊥BC,证明△DOM∽△EON;
(3)解Rt△EON和斜△AOM.
【解答】解:(1)OM=ON,
如图1,
作OD⊥AM于D,OE⊥CB于E,
∴∠ADO=∠MDO=∠CEO=∠OEN=90°,
∴∠DOE=90°,
∵AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°,
在Rt△AOD中,
OD=OA.sin∠A=OA.sin45°=OA,
同理:OE=OB,
∵OA=OB,
∴OD=OE,
∵∠DOE=90°,
∴∠DOM+∠MOE=90°,
∵∠MON=90°,
∴∠EON+∠MOE=90°,
∴∠DOM=∠EON,
在Rt△DOM和Rt△EON中,
,
∴△DOM≌△EON(ASA),
∴OM=ON.
(2)如图2,
作OD⊥AM于D,OE⊥BC于E,
由(1)知:OD=OA,OE=OB,
∴==,
由(1)知:
∠DOM=∠EON,∠MDO=∠NEO=90°,
∴△DOM∽△EON,
∴==,
∴ON=k•OM.
(3)如图3,
设AC=BC=a,
∴AB=a,
∵OB=k•OA,
∴OB=•a,OA=•a,
∴OE=OB=a,
∵∠N=∠ABC﹣∠BON=45°﹣15°=30°,
∴EN==OE=•a,
∵CE=OD=OA=a,
∴NC=CE+EN=a+•a,
由(2)知:==,△DOM∽△EON,
∴∠M=∠N
∵=,
∴=,
∴△PON∽△AOM,
∴∠P=∠A=45°,∠AMO=∠N=30°,
∴PE=OE=a,
∴PN=PE+EN=a+•a,
设AD=OD=x,
∴DM=,
由AD+DM=AC+CM得,
()x=AC+CM,
∴x=(AC+CM)<(AC+)=AC,
∴k>1
∴==,
∴=.
一十.相似三角形的判定与性质(共2小题)
16.(2022•朝阳)如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
(1)求证:AF是⊙O的切线;
(2)若⊙O的半径为5,AD是△AEF的中线,且AD=6,求AE的长.
【分析】(1)由圆周角定理得∠ADC=90°,则∠ACD+∠DAC=90°,从而说明OA⊥AF,即可证明结论;
(2)作DH⊥AC于点H,利用△ADH∽△ACD,得,求出AH的长,再利用直角三角形斜边上中线的性质得出AD=DE,利用等腰三角形的性质可得答案.
【解答】(1)证明:∵AC是直径,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵∠ACD=∠B,∠B=∠DAF,
∴∠DAF+∠DAC=90°,
∴OA⊥AF,
∵OA是半径,
∴AF是⊙O的切线;
(2)解:作DH⊥AC于点H,
∵⊙O的半径为5,
∴AC=10,
∵∠AHD=∠ADC,∠DAH=∠CAD,
∴△ADH∽△ACD,
∴,
∴AD2=AH•AC,
∴AH=,
∵AD是△AEF的中线,∠EAF=90°,
∴AD=ED,
∴AE=2AH=.
17.(2020•朝阳)如图,以AB为直径的⊙O经过△ABC的顶点C,过点O作OD∥BC交⊙O于点D,交AC于点F,连接BD交AC于点G,连接CD,在OD的延长线上取一点E,连接CE,使∠DEC=∠BDC.
(1)求证:EC是⊙O的切线;
(2)若⊙O的半径是3,DG•DB=9,求CE的长.
【分析】(1)连接OC,由AB是直径及OD∥BC可得∠CFE=∠ACB=90°,进而得到∠DEC+∠FCE=90°,再根据圆周角定理推导出∠DEC=∠A,进而得到OC⊥CE,再根据OC是半径即可得证;
(2)由(1)得∠CFE=90°,进而得到∠ACD=∠DBC,再通过证明△DCG∽△DBC得到DC2=DG•DB=9,再由即可求出CE的值.
【解答】解:(1)证明:如图,连接OC,
∵AB是直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠CFE=∠ACB=90°,
∴∠DEC+∠FCE=90°,
∵∠DEC=∠BDC,∠BDC=∠A,
∴∠DEC=∠A,
∵OA=OC,
∴∠OCA=∠A,
∴∠OCA=∠DEC,
∵∠DEC+∠FCE=90°,
∴∠OCA+∠FCE=90°,即∠OCE=90°,
∴OC⊥CE,
又∵OC是⊙O的半径,
∴CE是⊙O切线.
(2)由(1)得∠CFE=90°,
∴OF⊥AC,
∵OA=OC,
∴∠COF=∠AOF,
∴,
∴∠ACD=∠DBC,
又∵∠BDC=∠BDC,
∴△DCG∽△DBC,
∴,
∴DC2=DG•DB=9,
∴DC=3,
∵OC=OD=3,
∴△OCD是等边三角形,
∴∠DOC=60°,
在Rt△OCE中,
∴,
∴.
一十一.作图-位似变换(共1小题)
18.(2020•朝阳)如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图:
(1)以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1,请画出△A1B1C1;
(2)以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2,使它与△ABC的位似比为2:1.
【分析】(1)根据网格结构找出点A、B、C关于原点O为旋转中心的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)利用位似的性质,找出点A2、B2、C2的位置,然后画出图形即可.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
一十二.解直角三角形的应用-仰角俯角问题(共2小题)
19.(2022•朝阳)某数学兴趣小组准备测量校园内旗杆顶端到地面的高度(旗杆底端有台阶).该小组在C处安置测角仪CD,测得旗杆顶端A的仰角为30°,前进8m到达E处,安置测角仪EF,测得旗杆顶端A的仰角为45°(点B,E,C在同一直线上),测角仪支架高CD=EF=1.2m,求旗杆顶端A到地面的距离即AB的长度.(结果精确到1m.参考数据:≈1.7)
【分析】延长DF交AB于点G,根据题意可得:DF=CE=8m,DC=EF=BG=1.2m,∠AGF=90°,然后设AG=xm,在Rt△AFG中,利用锐角三角函数的定义求出FG的长,从而求出DG的长,再在Rt△ADG中,利用锐角三角函数的定义列出关于x的方程,进行计算即可解答.
【解答】解:延长DF交AB于点G,
由题意得:
DF=CE=8m,DC=EF=BG=1.2m,∠AGF=90°,
设AG=xm,
在Rt△AFG中,∠AFG=45°,
∴FG==x(m),
∴DG=DF+FG=(x+8)m,
在Rt△ADG中,∠ADG=30°,
∴tan30°===,
∴x=4+4,
经检验:x=4+4是原方程的根,
∴AB=AG+BG≈12(m),
∴旗杆顶端A到地面的距离即AB的长度约为12m.
20.(2021•朝阳)一数学兴趣小组去测量一棵周围有围栏保护的古树的高,在G处放置一个小平面镜,当一位同学站在F点时,恰好在小平面镜内看到这棵古树的顶端A的像,此时测得FG=3m,这位同学向古树方向前进了9m后到达点D,在D处安置一高度为1m的测角仪CD,此时测得树顶A的仰角为30°,已知这位同学的眼睛与地面的距离EF=1.5m,点B,D,G,F在同一水平直线上,且AB,CD,EF均垂直于BF,求这棵古树AB的高.(小平面镜的大小和厚度忽略不计,结果保留根号)
【分析】过点C作CH⊥AB于点H,则CH=BD,BH=CD=1m,由锐角三角函数定义求出BD=CH=AH,再证△EFG∽△ABG,得=,求出AH=(8+4)m,即可求解.
【解答】解:如图,过点C作CH⊥AB于点H,
则CH=BD,BH=CD=1m,
由题意得:DF=9m,
∴DG=DF﹣FG=6(m),
在Rt△ACH中,∠ACH=30°,
∵tan∠ACH==tan30°=,
∴BD=CH=AH,
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°.
由反射角等于入射角得∠EGF=∠AGB,
∴△EFG∽△ABG,
∴=,
即=,
解得:AH=(8+4)m,
∴AB=AH+BH=(9+4)m,
即这棵古树的高AB为(9+4)m.
一十三.解直角三角形的应用-方向角问题(共1小题)
21.(2020•朝阳)为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是30km/h,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由(结果保留根号).
【分析】过点B作BD⊥AC于D,在Rt△BCD中证得BD=CD,设BD=x,则CD=x,在Rt△ABD中,∠BAC=30°,利用三角函数定义表示出AD的长,在Rt△BDC中,利用三角函数表示出CD的长,由AD+CD=AC列出方程问题得解.
【解答】解:作BD⊥AC于D.
依题意得,
∠BAE=45°,∠ABC=105°,∠CAE=15°,
∴∠BAC=30°,
∴∠ACB=45°.
在Rt△BCD中,∠BDC=90°,∠ACB=45°,
∴∠CBD=45°,
∴∠CBD=∠DCB,
∴BD=CD,
设BD=x,则CD=x,
在Rt△ABD中,∠BAC=30°,
∴AB=2BD=2x,tan30°=,
∴,
∴AD=x,
在Rt△BDC中,∠BDC=90°,∠DCB=45°,
∴sin∠DCB=,
∴BC=x,
∵CD+AD=30+30,
∴x+,
∴x=30,
∴AB=2x=60,BC=,
第一组用时:60÷40=1.5(h);第二组用时:30(h),
∵<1.5,
∴第二组先到达目的地,
答:第一组用时1.5小时,第二组用时小时,第二组先到达目的地.
一十四.用样本估计总体(共1小题)
22.(2022•朝阳)为了解学生的睡眠情况,某校随机抽取部分学生对他们最近两周的睡眠情况进行调查,得到他们每日平均睡眠时长x(单位:h)的一组数据,将所得数据分为四组(A:x<8;B:8≤x<9;C:9≤x<10;D:x≥10),并绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)本次一共抽样调查了 50 名学生.
(2)求出扇形统计图中D组所对应的扇形圆心角的度数.
(3)将条形统计图补充完整.
(4)若该校共有1200名学生,请估计最近两周有多少名学生的每日平均睡眠时长大于或等于9h.
【分析】(1)由B组人数及其所占百分比求出总人数;
(2)用360°乘以D组人数所占比例即可;
(3)根据总人数求出A组人数,从而补全图形;
(4)用总人数乘以睡眠时长大于或等于9h人数所占比例即可.
【解答】解:(1)本次调查的学生人数为16÷32%=50(名),
故答案为:50;
(2)表示D组的扇形圆心角的度数为360°×=14.4°;
(3)A组人数为50﹣(16+28+2)=4(名),
补全图形如下:
(4)1200×=720(名).
答:估计该校最近两周有720名学生的每日平均睡眠时长大于或等于9h.
一十五.条形统计图(共2小题)
23.(2021•朝阳)“赏中华诗词,寻文化基因,品文学之美”,某校对全体学生进行了古诗词知识测试,将成绩分为一般、良好、优秀三个等级,从中随机抽取部分学生的测试成绩,根据调查结果绘制成两幅不完整的统计图,根据图中信息,解答下列问题:
(1)求本次抽样调查的人数;
(2)在扇形统计图中,阴影部分对应的扇形圆心角的度数是 90° ;
(3)将条形统计图补充完整;
(4)该校共有1500名学生,根据抽样调查的结果,请你估计测试成绩达到优秀的学生人数.
【分析】(1)由良好的人数除以占的百分比求本次抽样调查的人数;
(2)根据一般的人数所占百分比即可求出圆心角的度数;
(3)求出优秀的人数即可画出条形图;
(4)求出优秀占的百分比,乘以1500即可得到结果.
【解答】解:(1)总人数=50÷=120(人);
(2)阴影部分扇形的圆心角=360°×=90°,
故答案为:90°;
(3)优秀的人数为:120﹣30﹣50=40(人),
条形统计图如图所示:
(4)测试成绩达到优秀的学生人数有:1500×=500(人),
答:该校1500名学生中测试成绩达到优秀的学生有500人.
24.(2020•朝阳)由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如图两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 50 名学生;
(2)在扇形统计图中,m的值是 30 ,D对应的扇形圆心角的度数是 72° ;
(3)请补全条形统计图;
(4)若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式D的学生人数.
【分析】(1)用A的人数除以A的百分比即可;
(2)用B的人数除以样本容量即可;
(3)求出B的人数补全统计图即可;
(4)用2000乘以D的百分比即可.
【解答】解:(1)20÷40%=50(名);
故答案为:50;
(2)15÷50×100%=30%,即m=30;=72°;
故答案为:30,72°;
(3)50﹣20﹣15﹣10=5(名);
(4)(名).
答:该校最喜欢方式D的学生约有400名.
一十六.列表法与树状图法(共3小题)
25.(2022•朝阳)某社区组织A,B,C,D四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.
(1)王明被安排到A小区进行服务的概率是 .
(2)请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.
【分析】(1)根据概率公式求解即可;
(2)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解答】解:(1)王明被安排到A小区进行服务的概率是,
故答案为:;
(2)列表如下:
A
B
C
D
A
(A,A)
(B,A)
(C,A)
(D,A)
B
(A,B)
(B,B)
(C,B)
(D,B)
C
(A,C)
(B,C)
(C,C)
(D,C)
D
(A,D)
(B,D)
(C,D)
(D,D)
由表知,共有16种等可能结果,其中王明和李丽被安排到同一个小区工作的有4种结果,
所以王明和李丽被安排到同一个小区工作的概率为=.
26.(2021•朝阳)为了迎接建党100周年,学校举办了“感党恩•跟党走”主题社团活动,小颖喜欢的社团有写作社团、书画社团、演讲社团、舞蹈社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片正面,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小颖从中随机抽取一张卡片是舞蹈社团D的概率是 ;
(2)小颖先从中随机抽取一张卡片,记录下卡片上的字母不放回,再从剩下的卡片中随机抽取一张卡片,记录下卡片上的字母,请用列表法或画树状图法求出小颖抽取的两张卡片中有一张是演讲社团C的概率.
【分析】(1)共有4种可能出现的结果,其中是舞蹈社团D的有一种,即可求出概率;
(2)用列表法列举出所有可能出现的结果,从中找出一张是演讲社团C的结果数,进而求出概率.
【解答】解:(1)∵共有4种可能出现的结果,其中是舞蹈社团D的有1种,
∴小颖从中随机抽取一张卡片是舞蹈社团D的概率是,
故答案为:;
(2)用列表法表示所有可能出现的结果如下:
共有12种可能出现的结果,每种结果出现的可能性相同,其中有一张是演讲社团C的有6种,
∴小颖抽取的两张卡片中有一张是演讲社团C的概率是=.
27.(2020•朝阳)某校准备组建“校园安全宣传队”,每班有两个队员名额,七年2班有甲、乙、丙、丁四位同学报名,这四位同学综合素质都很好,王老师决定采取抽签的方式确定人选.具体做法是:将甲、乙、丙、丁四名同学分别编号为1、2、3、4号,将号码分别写在4个大小、质地、形状、颜色均无差别的小球上,然后把小球放入不透明的袋子中,充分搅拌均匀后,王老师从袋中随机摸出两个小球,根据小球上的编号确定本班“校园安全宣传员”人选.
(1)用画树状图或列表法,写出“王老师从袋中随机摸出两个小球”可能出现的所有结果.
(2)求甲同学被选中的概率.
【分析】(1)用树状图表示出所有可能的结果;
(2)从树状图中找到甲同学被选中的情况数,利用所求情况数与总数之比求概率即可.
【解答】解:画出树状图如图:
(1,2)(1,3)(1,4)(2,1)(2,3)(2,4)(3,1)(3,2)(3,4)(4,1)(4,2)(4,3)
∴“王老师从袋中随机摸出两个小球”可能出现的所有结果为:(1,2)(1,3)(1,4)(2,3)(2,4)(3,4),
∴所有可能出现的结果共有6种,每种结果出现的可能性相同,
(2)所有可能出现的结果共有6种,甲被选中的结果共有3种,
∴P(甲被选中)==.
辽宁省朝阳市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类: 这是一份辽宁省朝阳市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类,共40页。试卷主要包含了之间符合一次函数关系,如图所示,,与y轴交于点C,连接BC,,连接BC,【思维探究】等内容,欢迎下载使用。
辽宁省朝阳市2021-2023三年中考数学真题分类汇编-03解答题(基础题)知识点分类: 这是一份辽宁省朝阳市2021-2023三年中考数学真题分类汇编-03解答题(基础题)知识点分类,共14页。试卷主要包含了﹣2,÷,其中x=3,÷,其中x=tan60°等内容,欢迎下载使用。
辽宁省鞍山市三年(2020-2022)中考数学真题分类汇编-03解答题: 这是一份辽宁省鞍山市三年(2020-2022)中考数学真题分类汇编-03解答题,共58页。试卷主要包含了,其中m=2,÷,其中a=+2,÷,其中x=﹣2,,与x轴交于点C,,连接BC等内容,欢迎下载使用。












