初中数学人教版八年级下册18.2.3 正方形教学课件ppt

这是一份初中数学人教版八年级下册18.2.3 正方形教学课件ppt，共40页。PPT课件主要包含了素养目标，情境一观察体会，正方形的定义，正方形，思考1，一个角，是直角，轴对称图形，正方形的性质，平行四边形等内容，欢迎下载使用。
　除了矩形和菱形外，还有什么特殊的平行四边形呢？　　　
　 怎样研究这类图形？　想一想我们是怎样研究矩形和菱形的.
1. 理解正方形与平行四边形、矩形、菱形概 念之间的联系和区别.
2. 能用正方形的定义、性质进行推理与计算.
你能给正方形下一个定义吗？
问题1 图中CD在平移时，这个图形始终是怎样的图形？
问题2 当CD移动到CD位置，此时AD ＝AB，四边形ABCD还是矩形吗？
正方形是特殊的矩形.
情景二：两组互相垂直的平行线围成矩形ABCD
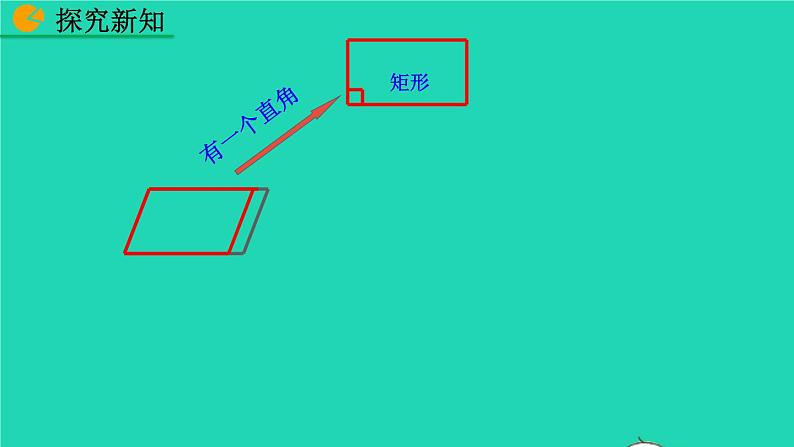
矩形一组邻边相等时变成怎样的图形呢?
【思考】2.菱形有一个角是直角时变成怎样的图形呢?
发现： 一组邻边相等的矩形叫正方形.
发现： 一个角为直角的菱形叫正方形.
如何来给正方形下定义？
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
请同学们拿出准备好的正方形纸片,折一折,观察并思考.正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性： .对称轴：.
总结：平行四边形、矩形、菱形、正方形的对称性
中心对称图形（对角线的交点）
即是中心对称图形，又是轴对称图形（两条）
即是中心对称图形，又是轴对称图形（四条）
有一组邻边相等且有一个角是直角
平行四边形、矩形、菱形、正方形之间关系：
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
性质：1.正方形的四个角都是直角,四条边相等. 2.正方形的对角线相等且互相垂直平分.
已知：如图,四边形ABCD是正方形.求证：正方形ABCD四边都相等,四个角都是直角.
证明：∵四边形ABCD是正方形.∴∠A=90°, AB=BC （正方形的定义）. 又∵正方形是平行四边形.∴正方形是矩形（矩形的定义）, 正方形是菱形(菱形的定义).∴∠A=∠B =∠C =∠D = 90°, AB= BC=CD=AD.
已知：如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证：AO=BO=CO=DO,AC⊥BD.
证明：∵正方形ABCD是矩形, ∴AO=BO=CO=DO.∵正方形ABCD是菱形.∴AC⊥BD.
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证:△ABO、△BCO、△CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,∴ AC=BD,AC⊥BD,AO=BO=CO=DO.∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且△ABO≌ △BCO ≌ △CDO ≌ △DAO.
利用正方形的性质求线段相等
已知正方形ABCD，若E为对角线上一点，连接EA、EC. EA = EC吗？说说你的理由.
解： EA = EC .理由如下：∵四边形ABCD是正方形，∴AB=BC，∠1=∠2=45°，又∵BE=BE,∴△ABE≌△CBE(SAS).∴AE=CE.
例2 如图，在正方形ABCD中， ΔBEC是等边三角形， 求证： ∠EAD＝∠EDA＝15° .
证明：∵ ΔBEC是等边三角形，∴BE=CE=BC,∠EBC=∠ECB=60°，∵ 四边形ABCD是正方形，∴AB=BC=CD,∠ABC=∠DCB=90°，∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°，∴△ABE，△DCE是等腰三角形，∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°，∴∠EAD= ∠EDA=90°-75°=15°.
利用正方形的性质求角度
已知：如图，在正方形ABCD中，F为CD延长线上一点，CE⊥AF于E，交AD于M， 求证：∠MFD＝45°.
证明：∵CE⊥AF， ∴∠ADC＝∠AEM＝90°. 又∵∠CMD＝∠AME， ∴∠1＝∠2.　 又∵CD＝AD，∠ADF＝∠MDC,　 ∴Rt△CDM≌Rt△ADF(ASA). ∴DM=DF. ∴∠DMF=∠DFM. ∵∠ADF=90°，∴∠MFD=45°.
例3 如图四边形ABCD和DEFG都是正方形，试说明AE=CG.
∵四边形ABCD是正方形,
又∵四边形DEFG也是正方形,
又∵正方形的每个内角为90°,
∴∠ADE＋∠EDC＝∠CDG＋∠EDC，
∴∠ADE＝∠CDG.
∴△AED≌△CGD(SAS).
利用正方形的性质证明线段相等
已知：如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且DE=BF．求证：（1）AE=AF；（2）EA⊥AF．
证明：（1）∵ ABCD是正方形,∴AD=AB，∠ADE=∠ABF=90°.在△ABF与△ADE中，AD=AB,∠ADE=∠ABF=90°，DE=BF,∴ △ABF≌△ADE（SAS）.∴ AE=AF ,∠1=∠3.（2）∵∠2+∠3=90 °,∴∠1+∠2=90 °即 EA⊥FA.
如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE≌△BCF．
证明：∵四边形ABCD是正方形， ∴AB=BC，∠ABE=∠BCF=90°， 在△ABE和△BCF中， ∴△ABE≌△BCF（SAS）．
1.正方形具有而矩形不一定具有的性质是( ) A.四个角相等 B.对角线互相垂直平分 C.对角互补 D.对角线相等
2.正方形具有而菱形不一定具有的性质（ ） A.四条边相等 B.对角线互相垂直平分 C.对角线平分一组对角 D.对角线相等
3．在正方形ABC中,∠ADB= ,∠DAC= , ∠BOC= .4.在正方形ABCD中，E是对角线AC上一点，且AE=AB，则∠EBC的度数是 .
5.如图，四边形ABCD是正方形，对角线AC与BD相交于点O，AO＝2，求正方形的周长与面积．
∵四边形ABCD是正方形，∴AC⊥BD，OA＝OD＝2.在Rt△AOD中，由勾股定理，得∴正方形的周长为4AD＝ ， 面积为AD2＝8.
如图，在正方形ABCD中，P为BD上一点，PE⊥BC于E， PF⊥DC于F.试说明：AP=EF.
又∵PE⊥BC ， PF⊥DC,
∴∠FCE=90°， AC垂直平分BD,
∴四边形PECF是矩形,
四边形ABCD是正方形，以正方形ABCD的一边作等边△ADE，求∠BEC的大小．
解：当等边△ADE在正方形ABCD外部时，如图①， AB＝AE，∠BAE＝90°＋60°＝150°.∴∠AEB＝15°.∴∠BEC＝60°－15°－15°＝30°；
同理可得∠DEC＝15°.
当等边△ADE在正方形ABCD内部时，如图②，AB＝AE，∠BAE＝90°－60°＝30°，∴∠AEB＝75°.同理可得∠DEC＝75°.∴∠BEC＝360°－75°－75°－60°＝150°.综上所述，∠BEC的大小为30°或150°.