初中沪科版23.2解直角三角形及其应用说课课件ppt

这是一份初中沪科版23.2解直角三角形及其应用说课课件ppt，共23页。PPT课件主要包含了学习目标，导入新课，复习引入，讲授新课，典例精析，在Rt△ABC中，练一练，归纳总结，变式1，变式2等内容，欢迎下载使用。

1.掌握解直角三角形的概念；（重点）2.掌握解直角三角形的依据并能熟练解题. (重点、难点)
(1) 三边之间的关系:a2+b2=_____；
(2)锐角之间的关系：∠A+∠B=_____；
(3)边角之间的关系：sinA=_____，csA=_____，tanA=_____.
在Rt△ABC中，共有六个元素（三条边，三个角），其中∠C=90°，那么其余五个元素之间有怎样的关系呢？
例1 如图，在Rt△ABC中，∠C＝90°， ,求这个直角三角形的其他元素.
解：在Rt△ABC中，a2+b2=c2,
☆已知两边解直角三角形
在如图的Rt△ABC中，根据AC＝2.4，斜边AB＝6，你能求出这个直角三角形的其他元素吗？
☆已知一边及一锐角解直角三角形
例2 如图，在Rt△ABC中，∠C＝90°，∠B＝35°，b=20,解这个直角三角形(结果保留小数点后一位).
在图中的Rt△ABC中，根据∠A＝75°，斜边AB＝6，你能求出这个直角三角形的其他元素吗？
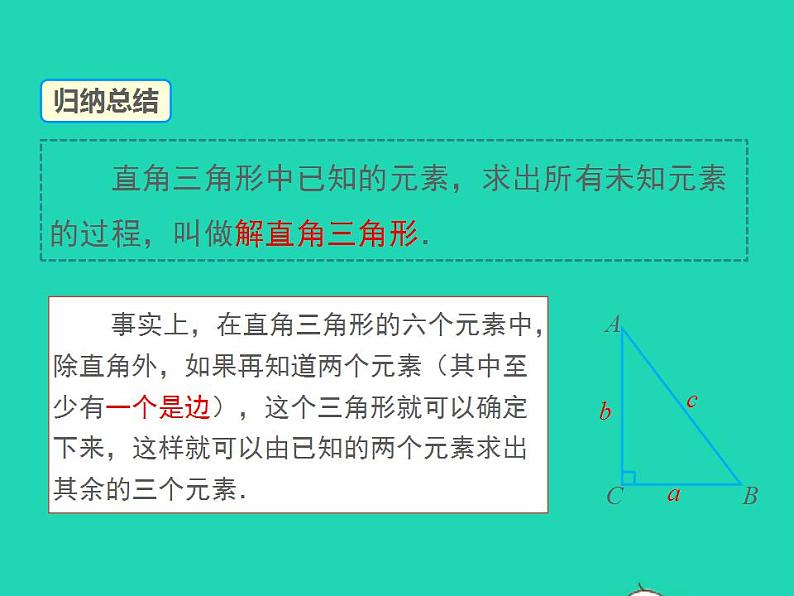
事实上，在直角三角形的六个元素中，除直角外，如果再知道两个元素（其中至少有一个是边），这个三角形就可以确定下来，这样就可以由已知的两个元素求出其余的三个元素．
直角三角形中已知的元素，求出所有未知元素的过程，叫做解直角三角形．
已知：如图Rt△ABC中，∠C=90°，∠A=45°，a=1，解这个直角三角形.
已知：如图Rt△ABC中，∠C=90°，a=1，b= 1，解这个直角三角形
已知：如图Rt△ABC中，∠C=90°，a=1，c= ，解这个直角三角形
☆构造直角三角形解决问题
例3 如图，在△ABC中，∠B=30°，∠C=45°，AC=2，求BC.
解：过点 A作 AD⊥BC于D.在△ACD中，∠C=45°，AC=2，∴CD=AD=sinC·AC=2sin45°= .在△ABD中，∠B=30°，∴BD=∴BC=CD+BD= + .
当△ABC为钝角三角形时，如图①，
∵AC=13，∴由勾股定理，得CD=5
∴BC=BD-CD=12-5=7；
当三角形的形状不确定时，一定要注意分类讨论.
当△ABC为锐角三角形时，如图②，BC=BD+CD=12+5=17.
∴BC的长为7或17.
2.如图，在菱形ABCD中，AE⊥BC于点E，EC=4， sinB＝ ，则菱形的周长是（　　） A．10 B．20 C．40 D．28
1.如图，在Rt△ABC中，∠C=90°，∠B=30°， AB=8，则BC的长是（　　）
3.在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形；（1）a = 30 , b = 20 ;
(2) ∠B＝72°，c = 14.
4. 如图，在Rt△ABC中，∠C＝90°，AC=6， ∠BAC的平分线 ，解这个直角三角形.
5. 如图，在Rt△ABC 中，∠C=90°，csA = ， BC = 5， 试求AB的长.
6. 如图，某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为多少米?
解：如图所示，依题意可知，当∠B=600 时，
答：梯子的长至少4.62米.
解法:只要知道五个元素中的两个元素（至少有一个是边），就可以求出余下的三个未知元素