【最新版】高中数学高三培优小题练第34练　三角函数小题综合练

这是一份【最新版】高中数学高三培优小题练第34练　三角函数小题综合练，共7页。试卷主要包含了已知点P在第三象限，则角α在，中国折叠扇有着深厚的文化底蕴等内容，欢迎下载使用。

A．第一象限 B．第二象限
C．第三象限 D．第四象限
答案 D
解析 ∵点P(tan α，sin α)在第三象限，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(tan α<0，,sin α<0，))
∴α在第四象限．
2．已知函数y＝f(x)＋cs x是奇函数，且f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)))＝1，则f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)))等于( )
A．－2 B．－1 C．1 D．2
答案 A
解析 根据题意，设g(x)＝f(x)＋cs x，则g(x)是奇函数，所以g(x)＋g(－x)＝0，
则geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)))＋geq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)))＝0，则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)))＋cs eq \f(π,3)＋f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)))＋cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)))＝0，即f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)))＝－2.
3．已知偶函数f(x)在(0，＋∞)上单调递减，若a＝tan 2，b＝tan 3，c＝tan 5，则下列不等关系正确的是( )
A．f(c)>f(b)>f(a)
B．f(c)>f(a)>f(b)
C．f(b)>f(a)>f(c)
D．f(b)>f(c)>f(a)
答案 C
解析 偶函数f(x)在(0，＋∞)上单调递减，
a＝tan 2，b＝tan 3，c＝tan 5，
则f(a)＝f(tan 2)＝f(tan(－2))＝f(tan(π－2)) ；
f(b)＝f(tan 3)＝f(tan(－3))＝f(tan(π－3))；
f(c)＝f(tan 5)＝f(tan(－5))＝f(tan(2π－5))；
易知0<π－3<π－2<2π－5故0故f(b)>f(a)>f(c)．
4．(2022·南昌模拟)已知sin α，cs α是方程2x2－x－m＝0的两个根，则m等于( )
A.eq \f(3,4) B．－eq \f(3,4) C.eq \f(1,2) D．－eq \f(1,2)
答案 A
解析 sin α，cs α是方程2x2－x－m＝0的两个根，
可得eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ＝1＋8m≥0，,sin α＋cs α＝\f(1,2)，,sin α·cs α＝－\f(m,2)，))
由eq \b\lc\(\rc\)(\a\vs4\al\c1(sin α＋cs α))2＝1＋2sin αcs α＝eq \f(1,4)，
得sin αcs α＝－eq \f(3,8)＝－eq \f(m,2)，解得m＝eq \f(3,4).
5．(2022·成都模拟)已知taneq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,4)))＝－3，则sin 2α等于( )
A.eq \f(4,5) B.eq \f(2,5)
C．－eq \f(4,5) D．－eq \f(4\r(5),5)
答案 A
解析 ∵taneq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,4)))＝－3，
∴tan α＝taneq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1( α＋\f(π,4)))－\f(π,4)))
＝eq \f(－3－1,1＋－3×1)＝2，
∴sin 2α＝2sin αcs α＝eq \f(2sin αcs α,sin2α＋cs2α)
＝eq \f(2tan α,1＋tan2α)＝eq \f(2×2,1＋4)＝eq \f(4,5).
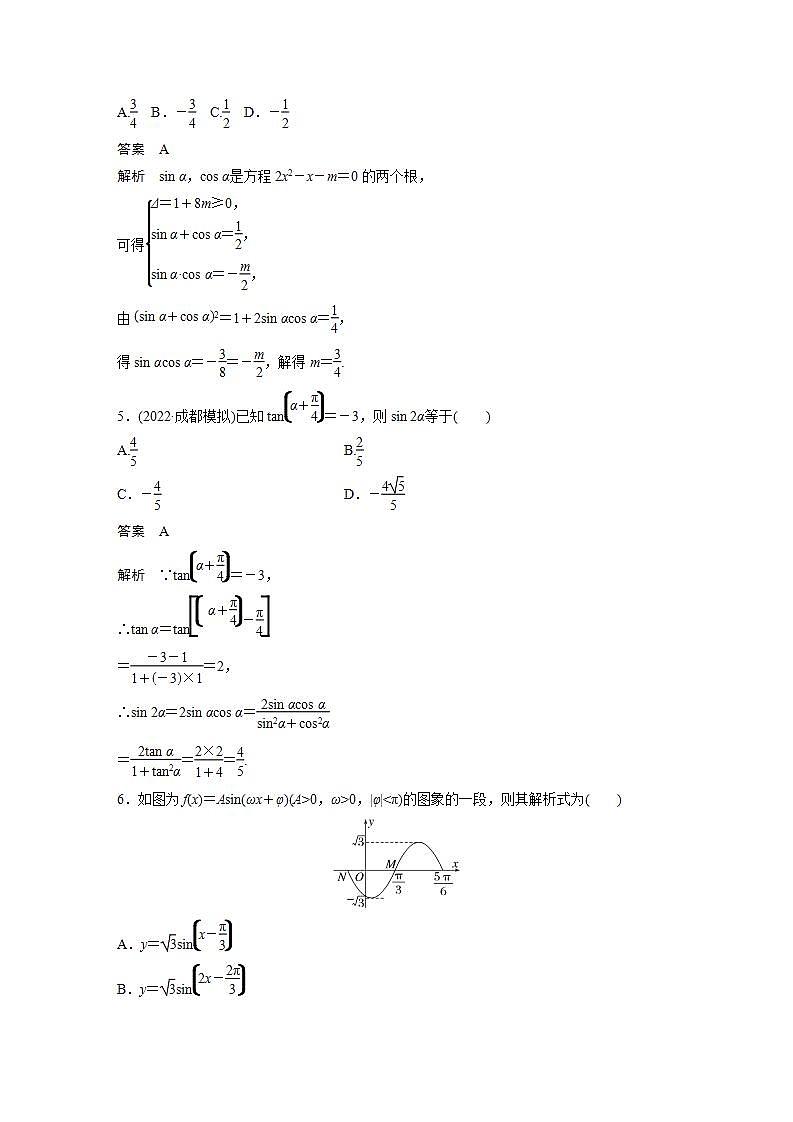
6．如图为f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<π)的图象的一段，则其解析式为( )
A．y＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))
B．y＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(2π,3)))
C．y＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))
D．y＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))
答案 B
解析 观察图象可知，A＝eq \r(3)，ω＝2，将Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)，0))代入f(x)＝eq \r(3)sin(2x＋φ)，
得eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(π,3)＋φ))＝0,2×eq \f(π,3)＋φ＝2kπ，k∈Z，解得φ＝2kπ－eq \f(2π,3)，k∈Z, 又|φ|<π，所以取φ＝－eq \f(2π,3)，
故y＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(2π,3))).
7．将函数f(x)＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,6)))的图象向右平移eq \f(π,6)个单位长度得到函数g(x)的图象，则( )
A．g(x)是奇函数
B．g(x)是偶函数
C．g(x)的图象的一条对称轴为直线x＝－eq \f(π,18)
D．g(x)的图象的一个对称中心为点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,18)，0))
答案 C
解析 由题意，
函数f(x)＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,6)))的图象向右平移eq \f(π,6)个单位长度，
得到函数g(x)＝3sineq \b\lc\[\rc\](\a\vs4\al\c1(3\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)))＋\f(π,6)))
＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,3))).
由三角函数的性质，可得g(x)为非奇非偶函数，所以A，B不正确；
令x＝－eq \f(π,18)，得3×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,18)))－eq \f(π,3)＝－eq \f(π,2)，所以直线x＝－eq \f(π,18)是函数g(x)图象的一条对称轴，所以C正确；
当x＝eq \f(5π,18)时，3×eq \f(5π,18)－eq \f(π,3)＝eq \f(π,2)，
此时geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,18)))＝3sin eq \f(π,2)＝3，所以D不正确．
故选C.
8．在△ABC中，A，B，C满足cs Acs Bcs C>0，则此三角形的形状是( )
A．锐角三角形
B．钝角三角形
C．直角三角形
D．可能是锐角三角形也可能是钝角三角形
答案 A
解析 因为cs Acs Bcs C>0，
所以cs A，cs B，cs C三者中，同为正或两负一正，
因为A，B，C为三角形的内角，
所以cs A，cs B，cs C三者中，同为正，
即A，B，C均为锐角．
9．中国折叠扇有着深厚的文化底蕴．如图(2)，在半圆O中作出两个扇形OAB和OCD，用扇环形ABDC(图中阴影部分)制作折叠扇的扇面．记扇环形ABDC的面积为S1，扇形OAB的面积为S2，当S1与S2的比值为eq \f(\r(5)－1,2)时，扇面的形状较为美观，则此时扇形OCD的半径与半圆O的半径之比为( )
图(1) 图(2)
A.eq \f(\r(5)＋1,4) B.eq \f(\r(5)－1,2)
C．3－eq \r(5) D.eq \r(5)－2
答案 B
解析 设∠AOB＝θ，半圆O的半径为r，扇形OCD的半径为r1，
依题意，有eq \f(\f(1,2)θr2－\f(1,2)θr\\al(2,1),\f(1,2)θr2)＝eq \f(\r(5)－1,2)，即eq \f(r2－r\\al(2,1),r2)＝eq \f(\r(5)－1,2)，
所以eq \f(r\\al(2,1),r2)＝eq \f(3－\r(5),2)＝eq \f(6－2\r(5),4)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(5)－1,2)))2，得eq \f(r1,r)＝eq \f(\r(5)－1,2).
10．(2022·济南模拟)如图，摩天轮的半径为40 m，其中心O点距离地面的高度为50 m，摩天轮按逆时针方向做匀速转动，且20 min转一圈，若摩天轮上点P的起始位置在最高点处，则摩天轮转动过程中，下列说法不正确的是( )
A．经过10 min点P距离地面10 m
B．若摩天轮转速减半，则其周期变为原来的eq \f(1,2)倍
C．第17 min和第43 min时P点距离地面的高度相同
D．摩天轮转动一圈，P点距离地面的高度不低于70 m的时间为eq \f(20,3) min
答案 B
解析 由题意知，可以以点O为原点，建立如图所示的平面直角坐标系，
设转动的时间为t min，点P距离地面的高度h(t)＝Asin(ωt＋φ)＋50，其中|φ|≤eq \f(π,2)，ω>0.
由题意得A＝40，函数h(t)的最小正周期T＝20，得ω＝eq \f(2π,20)＝eq \f(π,10)，又当t＝0时，h(t)＝90，所以φ＝eq \f(π,2)，
所以h(t)＝40sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,10)t＋\f(π,2)))＋50，
化简得h(t)＝40cseq \f(π,10)t＋50.
当t＝10时，h(t)＝10，故A正确；
若摩天轮转速减半，T＝40，则其周期变为原来的2倍，故B错误；
第17 min时P点距离地面的高度为heq \b\lc\(\rc\)(\a\vs4\al\c1(17))＝40cs eq \f(17π,10)＋50＝40cs eq \f(3π,10)＋50，
第43 min时P点距离地面的高度为heq \b\lc\(\rc\)(\a\vs4\al\c1(43))＝40cs eq \f(43π,10)＋50＝40cs eq \f(3π,10)＋50，
所以第17 min和第43 min时P点距离地面的高度相同，故C正确；
摩天轮转动一圈，P点距离地面的高度不低于70 m，即40cs eq \f(π,10)t＋50≥70，
即cs eq \f(πt,10)≥eq \f(1,2)，由0≤t≤20，得0≤eq \f(πt,10)≤2π，
所以0≤eq \f(πt,10)≤eq \f(π,3)或eq \f(5π,3)≤eq \f(πt,10)≤2π，
解得0≤t≤eq \f(10,3)或eq \f(50,3)≤t≤20，共eq \f(20,3) min，故D正确．
11．(2022·长春模拟)已知点Peq \b\lc\(\rc\)(\a\vs4\al\c1(sin \f(2π,3)，cs \f(2π,3)))落在角θ的终边上，则tan θ＝________.
答案 －eq \f(\r(3),3)
解析 由题设，Peq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)，－\f(1,2)))，又P落在角θ的终边上，
∴tan θ＝eq \f(－\f(1,2),\f(\r(3),2))＝－eq \f(\r(3),3).
12．若2cs 2θ＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(θ＋\f(π,4)))，且θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))，则sin 2θ的值为________．
答案 －eq \f(7,8)
解析 因为2cs 2θ＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(θ＋\f(π,4)))，
故2eq \b\lc\(\rc\)(\a\vs4\al\c1(cs2θ－sin2θ))＝eq \f(\r(2),2)eq \b\lc\(\rc\)(\a\vs4\al\c1(cs θ－sin θ)).
因为θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))，故cs θ－sin θ≠0，
所以2eq \b\lc\(\rc\)(\a\vs4\al\c1(cs θ＋sin θ))＝eq \f(\r(2),2).
即cs θ＋sin θ＝eq \f(\r(2),4)，两边平方得1＋sin 2θ＝eq \f(1,8).
故sin 2θ＝－eq \f(7,8).
13．关于x的方程eq \r(3)sin x＋cs x＋a＝0在0≤x≤eq \f(π,2)上有两个不同的解，则a的取值范围是________．
答案 (－2，－eq \r(3)]
解析 eq \r(3)sin x＋cs x＝－a化简得2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))＝－a.
∵x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))，
∴x＋eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3)))，
令t＝x＋eq \f(π,6)，
∵关于x的方程eq \r(3)sin x＋cs x＋a＝0在0≤x≤eq \f(π,2)上有两个不同的解，
∴函数y＝2sin t，t∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3)))与函数y＝－a的图象有两个不同的交点，
函数y＝2sin t，t∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3)))与函数y＝－a的图象如图所示．
由图可知，要使得函数y＝2sin t，t∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3)))与函数y＝－a的图象有两个不同的交点，则eq \r(3)≤－a<2，即－214．已知函数f(x)＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))eq \b\lc\(\rc\)(\a\vs4\al\c1(0≤x≤\f(91π,6)))，若函数F(x)＝f(x)－3的所有零点依次记为x1，x2，x3，…，xn，且x1答案 445π
解析 令2x＋eq \f(π,6)＝eq \f(π,2)＋kπ，k∈Z，解得x＝eq \f(π,6)＋eq \f(kπ,2)，k∈Z，故函数f(x)的图象在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(91π,6)))上的对称轴为x＝eq \f(π,6)，eq \f(2π,3)，…，eq \f(44π,3)，共有30条，所以x1＋x2＝2×eq \f(π,6)＝eq \f(π,3)，x2＋x3＝2×eq \f(2π,3)＝eq \f(4π,3)，x3＋x4＝2×eq \f(7π,6)＝eq \f(7π,3)，以此类推，xn－1＋xn＝2×eq \f(44π,3)＝eq \f(88π,3)，所以(x1＋x2)＋(x2＋x3)＋…＋(xn－1＋xn)＝eq \f(30×\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)＋\f(88π,3))),2)＝445π.