


人教版数学八年级上册-第十二章 全等三角形 复习课件(共30张PPT)
展开知识回顾——全等三角形
能够完全重合的两个三角形叫做全等三角形。
全等三角形的对应边、对应角相等。
3、一个图形经过平移、翻折、旋转后,位置发生了变化,但是它的形状和大小并没有改变。即:平移、翻折、 旋转前后的两个图形全等。
1、有公共边的,公共边是对应边;2、有公共角的,公共角是对应角;3、有对顶角的,对顶角是对应角;4、两个全等三角形最大的边是对应边,最小的边是对应边;5、两个全等三角形最大的角是对应角,最小的角是对应角;
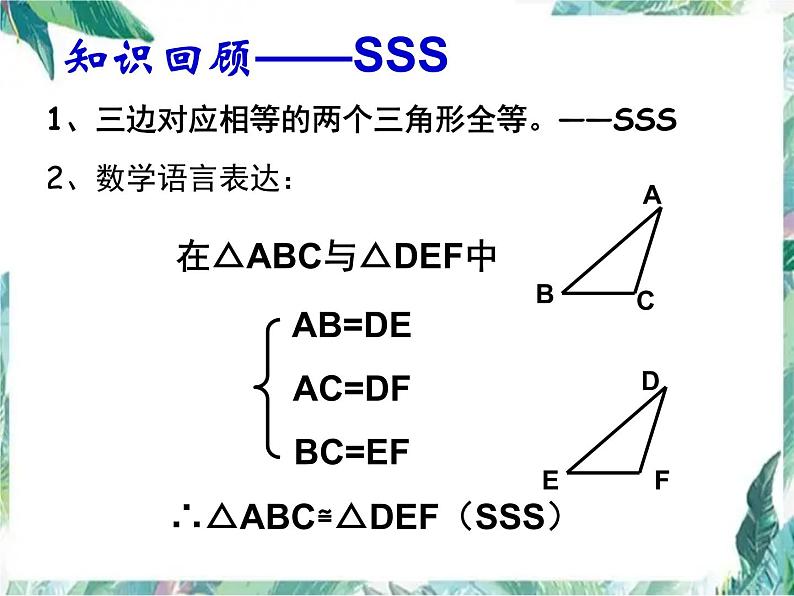
1、三边对应相等的两个三角形全等。——SSS
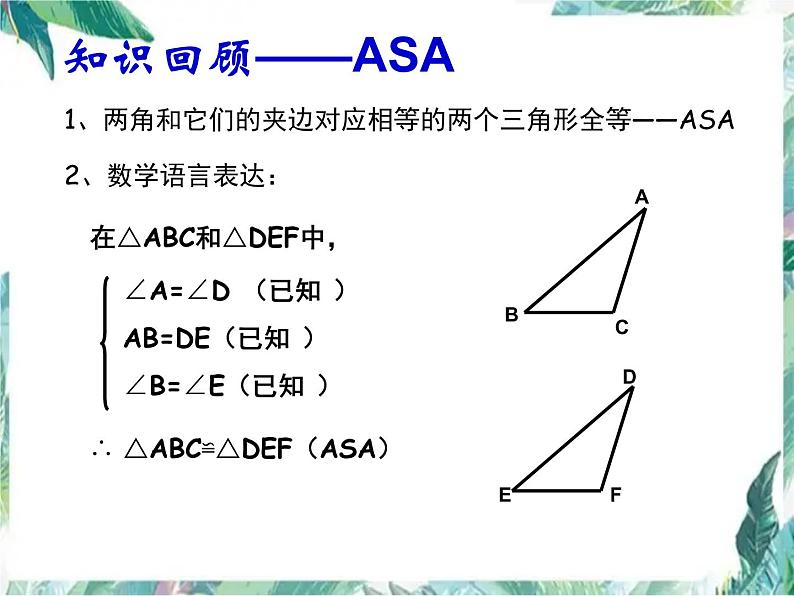
在△ABC与△DEF中
AB=DEAC=DFBC=EF
∴△ABC≌△DEF(SSS)
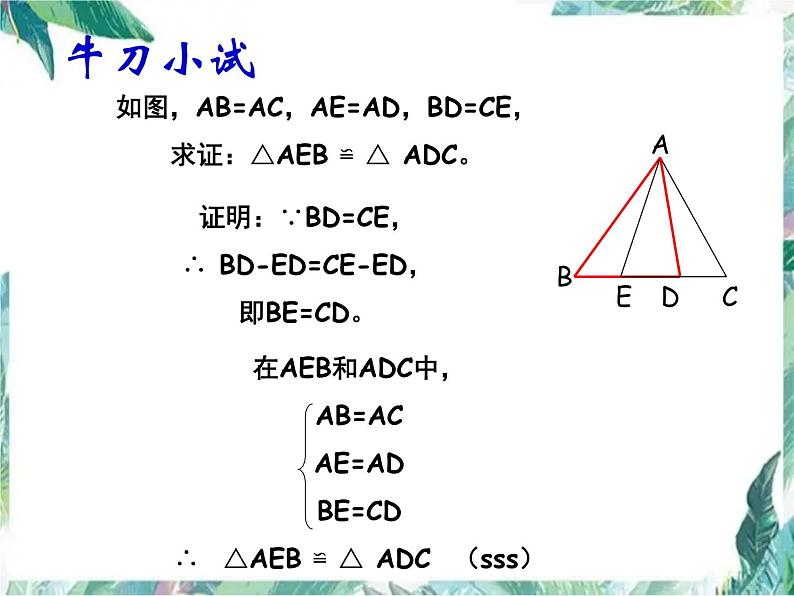
如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。
证明:∵BD=CE,∴ BD-ED=CE-ED,即BE=CD。
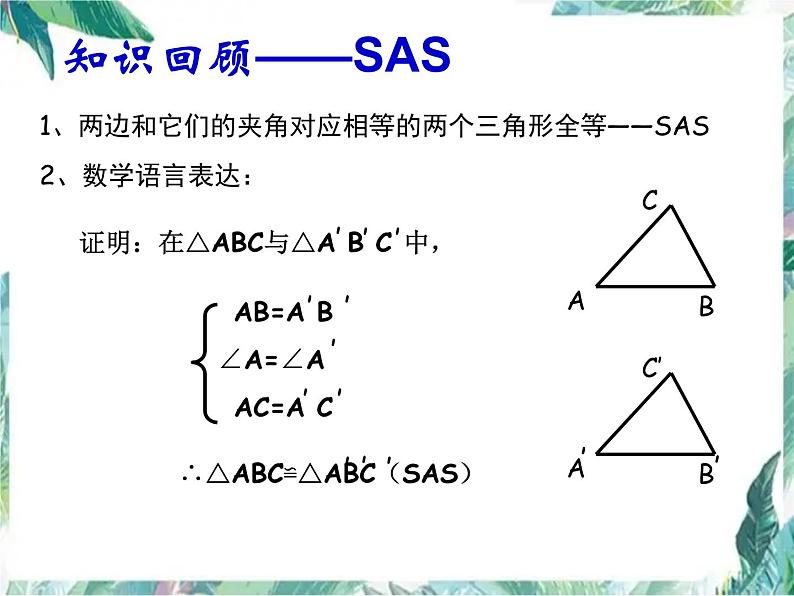
1、两边和它们的夹角对应相等的两个三角形全等——SAS
∴△ABC≌△ABC(SAS)
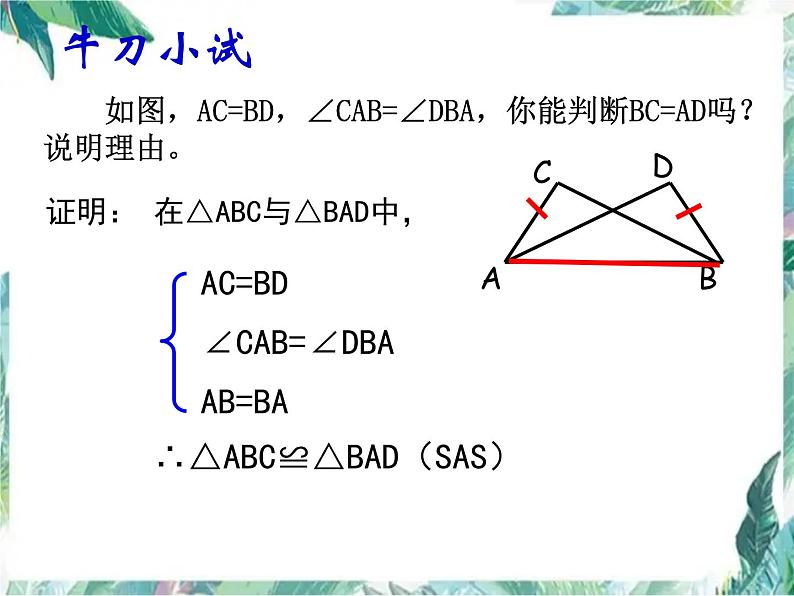
如图,AC=BD,∠CAB=∠DBA,你能判断BC=AD吗?说明理由。
证明: 在△ABC与△BAD中,
AC=BD∠CAB=∠DBAAB=BA
∴△ABC≌△BAD(SAS)
1、两角和它们的夹边对应相等的两个三角形全等——ASA
如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB = AC,∠B = ∠C。求证:BD = CE
1、两个角和其中一个角的对边对应相等的两个三角形全等——AAS
已知,如图,∠1=∠2,∠C=∠D,求证:AC=AD。
在△ABD和△ABC中,∠1=∠2 (已知)∠D=∠C(已知) AB=AB(公共边)∴△ABD≌△ABC (AAS)∴AC=AD (全等三角形对应边相等)
1、斜边和一条直角边对应相等的两个直角三角形全等——HL
∵∠C=∠C′=90°,
∴在Rt△ABC和Rt△ 中,
已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,垂足分别为C,D,AD=BC,求证:BD=AC。
证明:∵ AC⊥BC, AD⊥BD,∴∠C=∠D=90°,在Rt△ABC和Rt△BAD中,
∴ Rt△ABC≌Rt△BAD (HL)
(1)角的平分线上的点到角的两边的距离相等。
知识回顾——角平分线的性质1
如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E。求证PD=PE。
角的平分线上的点到角的两边的距离相等。
角的内部到角的两边的距离相等的点在角的平分线上。
应用:证明某条线是角平分线(证明角相等)。
如图PD=PE,PD⊥OA,PE⊥OB,垂足分别为D,E。求证∠1=∠2。
证明1:∵ PD⊥OA,PE⊥OB,∴ ∠ODP= ∠OEP=90°。在Rt△ODP和 Rt △OEP中, OP=OP PD=PE ∴ Rt △ODP≌ Rt △OEP(HL) ∴∠1=∠2。
证明2:∵PD⊥OA,PE⊥OB,PD=PE,∴∠1=∠2。
知识回顾——角平分线的性质2
如图,在△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC。
证明:过点D作DE⊥AB于E,DF⊥AC于F。
一般三角形 全等的条件:
直角三角形 全等特有的条件:
不包括其它形状的三角形
证明两个三角形全等的基本思路
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
已知角是直角,找一边(HL)
找两角的夹边(ASA)
找夹边外的任意边(AAS)
一、挖掘“隐含条件”判全等
1.如图(1),AB=CD,AC=BD,则△ABC≌△DCB吗?说说理由。
学习提示:公共边,公共角,对顶角这些都是隐含的边,角相等的条件!
4.如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”需要添加条件 ;根据“ASA”需要添加条件 ;根据“AAS”需要添加条件 ;
友情提示:添加条件的题目。首先要找到已具备的条件,这些条件有些是题目已知条件,有些是图中隐含条件。
三、熟练转化“间接条件”判全等
5.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△CEB全等吗?为什么?
解:∵AE=CF(已知),
∴AE-FE=CF-EF(等量减等量,差相等)。
在△AFD和△CEB中,
解:∵ ∠CAE=∠BAD(已知),
∴ ∠CAE+∠BAE=∠BAD+∠BAE,(等量加等量,和相等)
即∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌ △ADE
7.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。
∴△ADC≌△ABC(SSS)
∴ ∠ABC=∠ADC(全等三角形的对应角相等)。
在△ABC和△ADC中,
8 . 测量如图河的宽度,某人在河的对岸找到一参照物树木A,视线AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75m)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。
9.如图,ΔABC与ΔDEF是否全等?为什么?
已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,求证:BE=AD。
变式:以上条件不变,将△ABC绕点C旋转一定角度,以上的结论还成立吗?
学习全等三角形应注意以下几个问题:
(1)要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;
(2)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3)要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4)时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”。
人教版 数学八年级上册第十二章全等三角形复习课件: 这是一份人教版 数学八年级上册第十二章全等三角形复习课件
人教版八年级上册课件: 全等三角形复习 (共32张PPT): 这是一份人教版八年级上册课件: 全等三角形复习 (共32张PPT),共32页。PPT课件主要包含了全等三角形的应用,基础过关,ABAE,①ABAE,BCED,∠C∠D,③∠C∠D,∠B∠E,④EF∥BC,⑤AEDB等等内容,欢迎下载使用。
人教版 八年级数学上册第十二章:全等三角形复习课件(共15张PPT): 这是一份人教版 八年级数学上册第十二章:全等三角形复习课件(共15张PPT),共15页。PPT课件主要包含了知识点回顾,全等图形,全等三角形,能够完全重合的图形,形状相同大小相等,对应角相等,SAS,ASA,AAS,SSS等内容,欢迎下载使用。












