人教版八年级上册数学课件 第十二章 小结与复习(共31张PPT)

这是一份人教版八年级上册数学课件 第十二章 小结与复习(共31张PPT)，共31页。PPT课件主要包含了4性质，▼应用格式，▼用符号语言表达为，角的平分线的性质，OP平分∠AOB，PD⊥OA于D，PE⊥OB于E，PDPE，角的平分线的判定，∴GEGC等内容，欢迎下载使用。

1.能完全重合的两个三角形叫全等三角形.
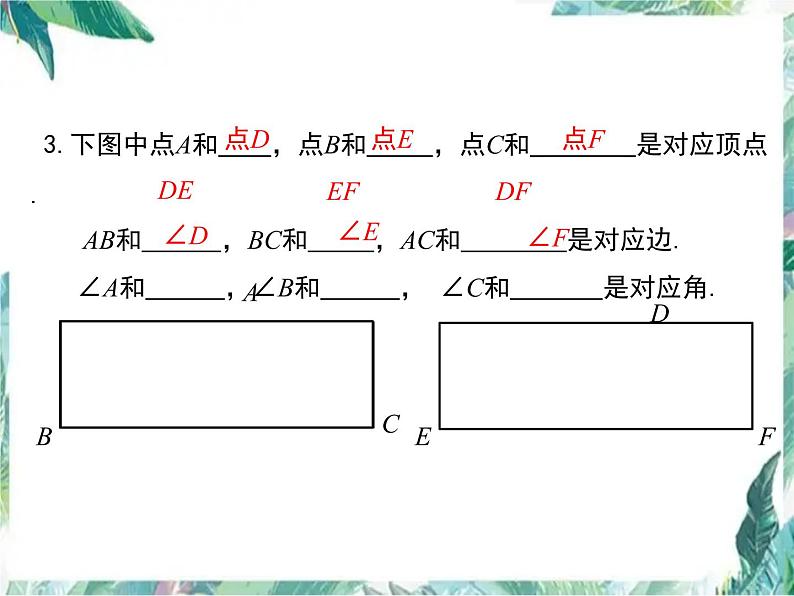
3.下图中点A和 ，点B和 ，点C和_ _是对应顶点. AB和 ，BC和 ，AC和 是对应边. ∠A和 ，∠B和 ， ∠C和 是对应角.
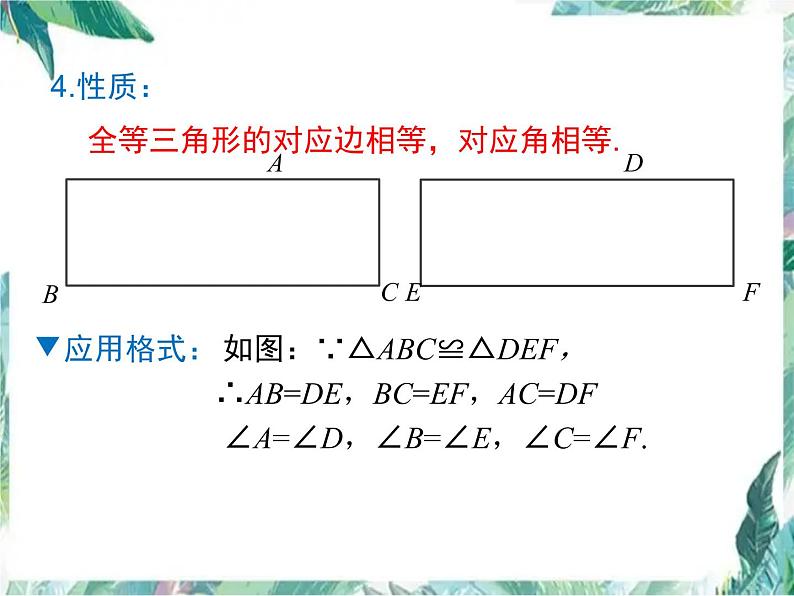
全等三角形的对应边相等，对应角相等.
如图：∵△ABC≌△DEF， ∴AB=DE，BC=EF，AC=DF ∠A=∠D，∠B=∠E，∠C=∠F.
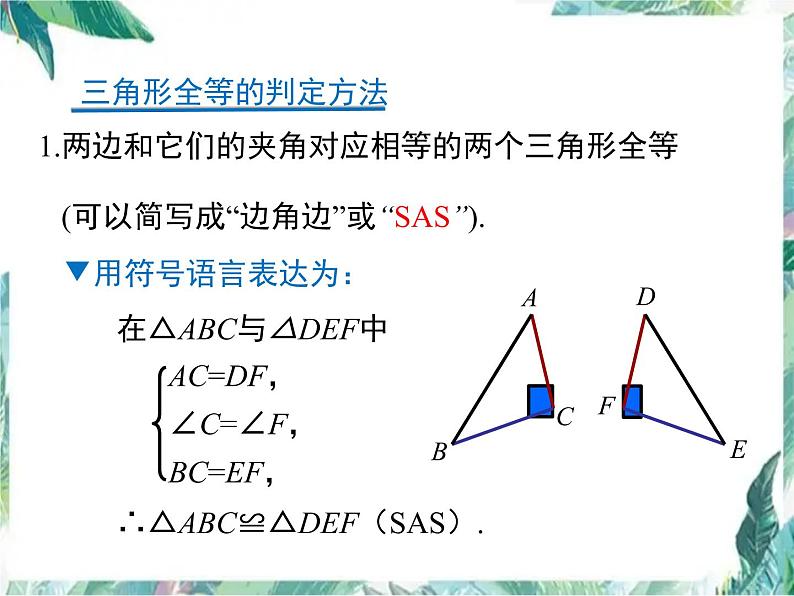
在△ABC与△DEF中
∴△ABC≌△DEF（SAS）.
1.两边和它们的夹角对应相等的两个三角形全等 (可以简写成“边角边”或“SAS”).
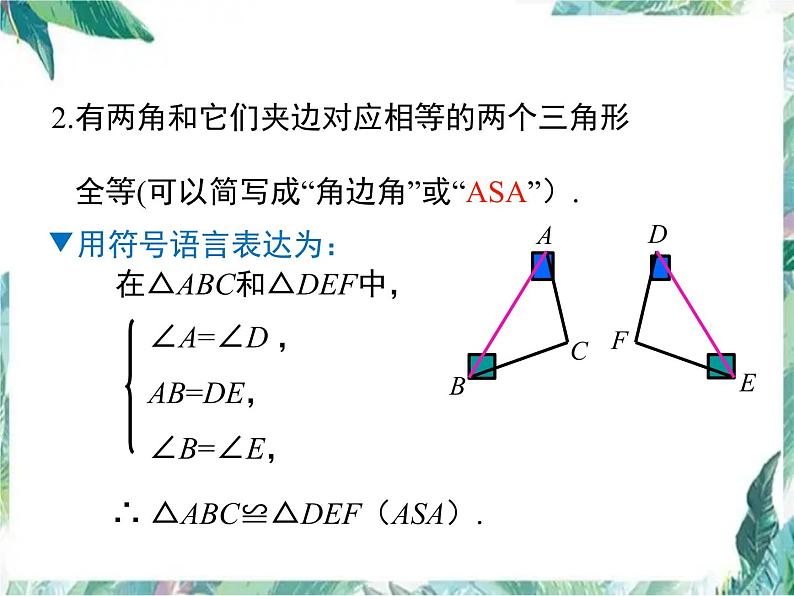
在△ABC和△DEF中，
∴ △ABC≌△DEF（ASA）.
2.有两角和它们夹边对应相等的两个三角形 全等(可以简写成“角边角”或“ASA”）.
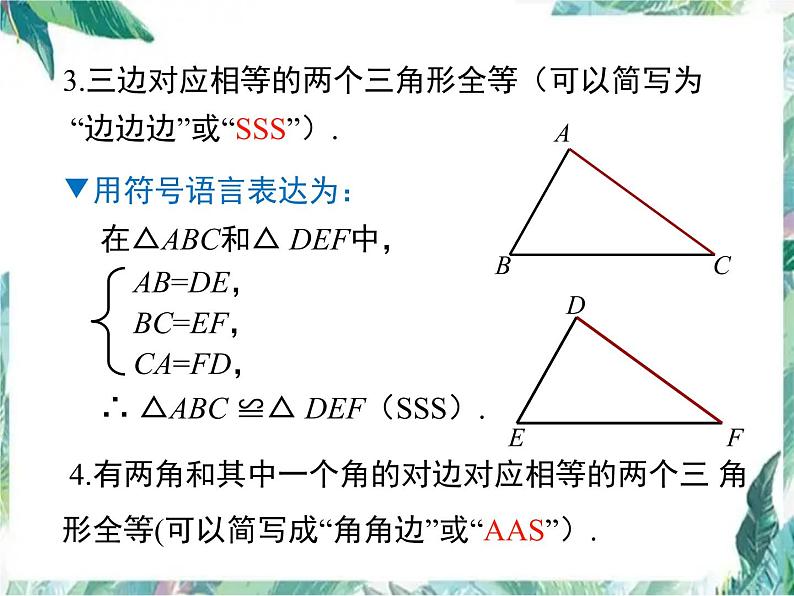
3.三边对应相等的两个三角形全等（可以简写为 “边边边”或“SSS”）.
在△ABC和△ DEF中，
∴ △ABC ≌△ DEF（SSS）.
4.有两角和其中一个角的对边对应相等的两个三 角形全等(可以简写成“角角边”或“AAS”）.
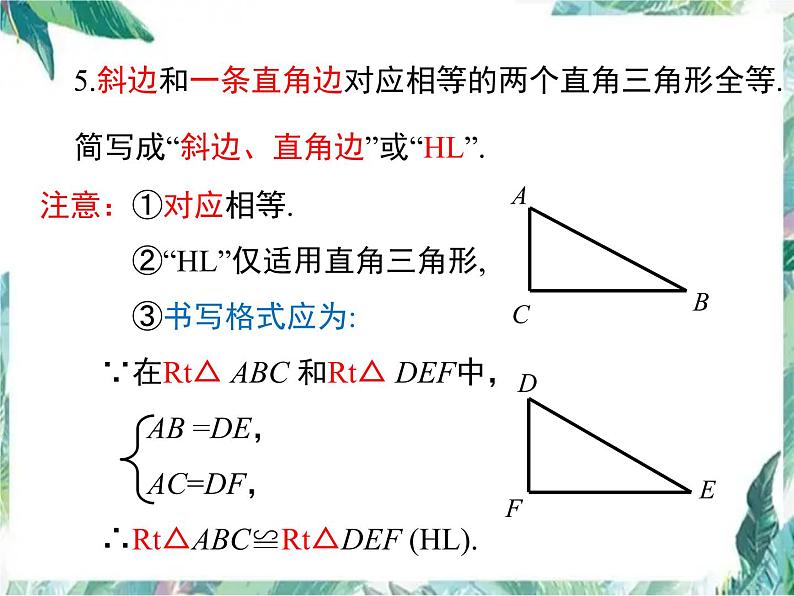
5.斜边和一条直角边对应相等的两个直角三角形全等. 简写成“斜边、直角边”或“HL”.
注意：①对应相等. ②“HL”仅适用直角三角形, ③书写格式应为: ∵在Rt△ ABC 和Rt△ DEF中， AB =DE， AC=DF， ∴Rt△ABC≌Rt△DEF (HL).
如图，已知△ACE≌△DBF，CE=BF，AE=DF，AD=8，BC=2．（1）求AC的长度；（2）试说明CE∥BF．
解：（1）∵△ACE≌△DBF，∴AC=BD，则AB=DC.∵BC=2，∴2AB+2=8，∴AB=3，∴AC=3+2=5.（2）∵△ACE≌△DBF，∴∠ECA=∠FBD，∴CE∥BF．
两个全等三角形的长边与长边，短边与短边分别是对应边，大角与大角，小角与小角分别是对应角.有对顶角的，两个对顶角一定为一对对应角.有公共边的，公共边一定是对应边.有公共角的，公共角一定是对应角.
练习1：如图所示，△ABD≌△ACD，∠BAC=90°．（1）求∠B； （2）判断AD与BC的位置关系，并说明理由．
解：（1）∵△ABD≌△ACD，∴∠B=∠C.又∵∠BAC=90°，∴∠B=∠C=45°.（2）AD⊥BC．理由：∵△ABD≌△ACD，∴∠BDA=∠CDA.∵∠BDA+∠CDA=180°，∴∠BDA=∠CDA=90°，∴AD⊥BC．
已知，∠ABC＝∠DCB，∠ACB＝ ∠DBC， 求证：△ABC≌△DCB．
∠ABC＝∠DCB， BC＝CB， ∠ACB＝∠DBC，
在△ABC和△DCB中，
∴△ABC≌△DCB（ASA ）.
分析：运用“两角和它们的夹边对应相等两个三角形全等”进行判定．
练习2：已知△ABC和△DEF,下列条件中,不能保证△ABC和△DEF全等的是( )A.AB=DE,AC=DF,BC=EF B. ∠A= ∠ D, ∠ B= ∠ E,AC=DFC.AB=DE,AC=DF, ∠A= ∠D D.AB=DE,BC=EF, ∠ C= ∠ F
如图，在△ABC中，AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,求证：∠DEC=∠FEC.
欲证∠DEC=∠FEC
由平行线的性质转化为证明∠DEC=∠DCE
转化为证明△DEG ≌ △DCG
证明： ∵CE⊥AD, ∴ ∠AGE=∠AGC=90 °.
在△AGE和△AGC中，
∴ △AGE ≌ △AGC(ASA)，
∵AD平分∠BAC,∴ ∠EAG=∠CAG.
在△DGE和△DGC中，
∴ △DGE ≌ △DGC(SAS).
∴ ∠DEG = ∠ DCG.
∴ ∠FEC= ∠ECD，
∴ ∠DEG = ∠ FEC.
利用全等三角形证明角相等，首先要找到两个角所在的两个三角形，看它们全等的条件够不够；有时会用到等角转换，等角转换的途径很多，如：余角、补角的性质，平行线的性质等，必要时要想到添加辅助线.
练习3：如图，OB⊥AB,OC⊥AC,垂足为B、C,OB=OC，∠BAO =∠CAO吗？为什么？
解： ∠BAO=∠CAO.
理由：∵ OB⊥AB,OC⊥AC， ∴ ∠B=∠C=90°. 在Rt△ABO和Rt△ACO中， OB=OC，AO=AO， ∴ Rt△ABO≌Rt△ACO （HL）， ∴ ∠BAO=∠CAO.
利用全等三角形解决实际问题
如图，两根长均为12米的绳子一端系在旗杆上，旗杆与地面垂直，另一端分别固定在地面上的木桩上，两根木桩离旗杆底部的距离相等吗？
分析：将本题中的实际问题转化为数学问题就是证明BD=CD.由已知条件可知AB=AC，AD⊥BC.
∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中，
∴ Rt△ADB ≌ Rt△ADC(HL).
利用全等三角形可以测量一些不易测量的距离和长度，还可对某些因素作出判断，一般采用以下步骤：（1）先明确实际问题；（2）根据实际抽象出几何图形；（3）经过分析，找出证明途径；（4）书写证明过程.
练习4：如图，有一湖的湖岸在A、B之间呈一段圆弧状，A、B间的距离不能直接测得．你能用已学过的知识或方法设计测量方案，求出A、B间的距离吗？
解：要测量A、B间的距离，可用如下方法：过点B作AB的垂线BF，在BF上取两点C、D，使CD=BC；再作出BF的垂线DE，使A、C、E在一条直线上.∵∠ACB=∠ECD，CB=CD，∠ABC=∠EDC，∴△EDC≌△ABC（ASA）．∴DE=BA．即测出DE的长就是A、B之间的距离．
角平分线的性质与判定
如图,∠1=∠2,点P为BN上的一点，∠PCB+ ∠BAP=180 °.求证:PA=PC.
分析：由角平分线的性质易想到过点P向∠ABC的两边作垂线段PE、PF，构造角平分线的性质与判断的基本图形.
证明：过点P作PE⊥BA,PF⊥BC,垂足分别为E、F.
∵∠1=∠2,PE⊥BA,PF⊥BC,垂足分别为E、F，
∴PE=PF, ∠PEA=∠PFC=90 °.
∵ ∠PCB+ ∠BAP=180 °,∠BAP+∠EAP=180 °.
∴ ∠EAP=∠PCB.
在△APE和△CPF中，
∴ △APE ≌ △CPF(AAS)，
方法2思路分析：由角是轴对称图形，其对称轴是角平分线所在的直线，所以可想到构造轴对称图形.方法是在BC上截取BD=AB,连接PD（如图）.则有△PAB≌△PDB,再证△PDC是等腰三角形即可获证.
证明过程请同学们自行完成！
归纳拓展：角的平分线的性质是证明线段相等的常用性质.应用时要依托全等三角形发挥作用.作辅助线有两种思路，一种作垂线段构造角平分线性质基本图；另一种是构造轴对称图形.
练习5：如图,∠1=∠2,点P为BN上的一点， PA=PC ，求证:∠PCB+ ∠BAP=180 °.
在Rt△APE和Rt△CPF中，
∴ Rt△PAE ≌ Rt△PCF(HL).
∴ ∠ EAP= ∠ FCP.
∵ ∠BAP+∠EAP=180 °，
∴ ∠PCB+ ∠BAP=180 °.
想一想：本题如果不给图，条件不变，请问∠PCB与∠PAB有怎样的数量关系呢？
基本性质和其他重要性质
是证明两条线段相等和角相等的常用方法
寻找现有条件（包括图中隐含条件）
选定判定方法证明准备条件