

2023届广西柳州市新高三摸底考试数学(文)试题含解析
展开广西柳州市2023届新高三摸底考试
数学(文)试题
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.设,若复数的虚部与复数的虚部相等,则( )
A. B. C. D.
3.已知向量,的夹角为,且,,则( )
A.-1 B. C.-2 D.1
4.某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( )
A.这五个社团的总人数为100
B.脱口秀社团的人数占五个社团总人数的20%
C.这五个社团总人数占该校学生人数的8%
D.从这五个社团中任选一人,其来脱口秀社团或舞蹈社团的概率为50%
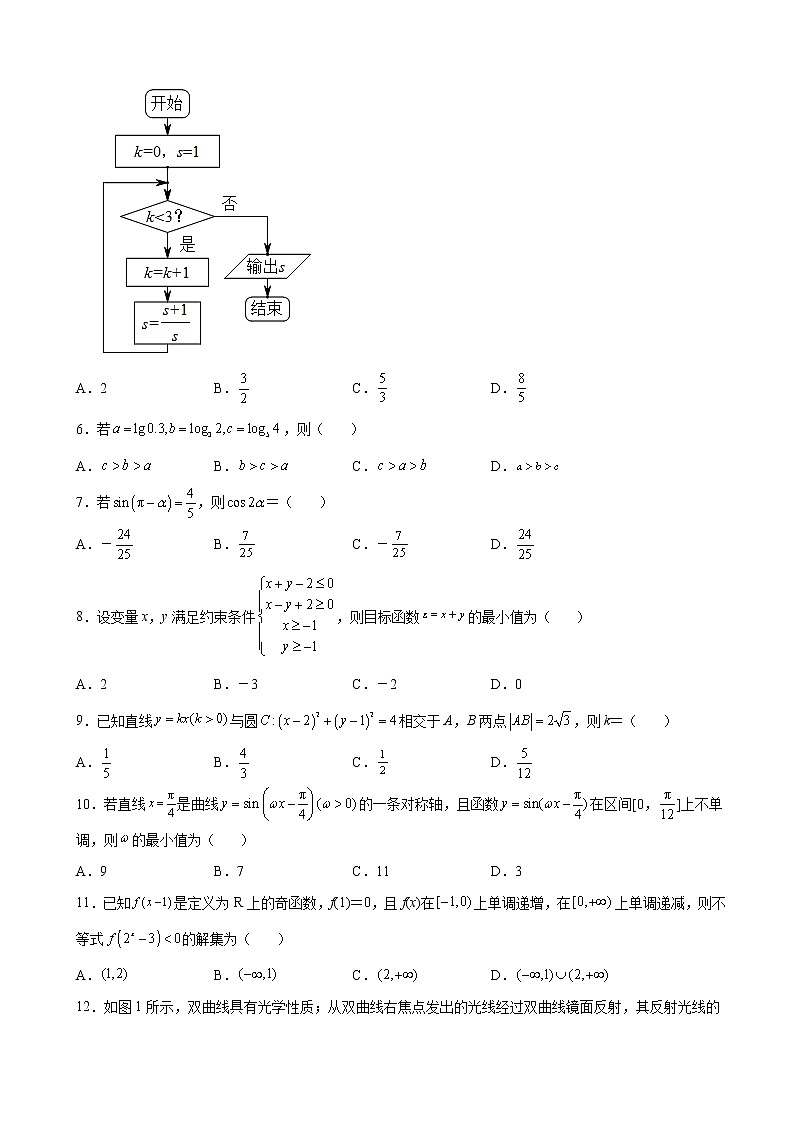
5.执行如图所示的程序框图,输出的s值为( )
A.2 B. C. D.
6.若,则( )
A. B. C. D.
7.若,则=( )
A.- B. C.- D.
8.设变量x,y满足约束条件,则目标函数的最小值为( )
A.2 B.-3 C.-2 D.0
9.已知直线与圆相交于A,B两点,则k=( )
A. B. C. D.
10.若直线是曲线的一条对称轴,且函数在区间[0,]上不单调,则的最小值为( )
A.9 B.7 C.11 D.3
11.已知是定义为R上的奇函数,f(1)=0,且f(x)在上单调递增,在上单调递减,则不等式的解集为( )
A. B. C. D.
12.如图1所示,双曲线具有光学性质;从双曲线右焦点发出的光线经过双曲线镜面反射,其反射光线的反向延长线经过双曲线的左焦点.若双曲线E:的左、右焦点分别为,,从发出的光线经过图2中的A,B两点反射后,分别经过点C和D,且,,则E的离心率为( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13.记等差数列的前n项和为,若,则___.
14.若函数,则在点处的切线方程为___.
15.已知是椭圆的左、右焦点,P在椭圆上运动,求的最小值为___.
16.在正方体中,点E为线段上的动点,现有下面四个命题:
①直线DE与直线AC所成角为定值;②点E到直线AB的距离为定值;
③三棱锥的体积为定值;④三棱锥外接球的体积为定值.
其中所有真命题的序号是______.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答
17.在锐角△ABC中,角A、B、C所对的边分别为a、b、c,已知.
(1)求角A的大小;
(2)若,,求△ABC的面积.
18.已知数列满足.
(1)证明是等比数列,并求的通项公式;
(2)求数列的前项和公式.
19.2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了200人进行调查,其中女生中对冰球运动有兴趣的占,而男生有20人表示对冰球运动没有兴趣.
(1)完成列联表,并回答能否有97.5%的把握认为“对冰球是否有兴趣与性别有关”?
| 有兴趣 | 没兴趣 | 合计 |
男 |
|
| 110 |
女 |
|
|
|
合计 |
|
|
|
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取2人,求至少有1人对冰球有兴趣的概率.
0.10 | 0.05 | 0.025 | 0.010 | |
2.706 | 3.841 | 5.024 | 6.635 |
.
20.如图,在三棱锥中,,,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.
21.已知函数.
(1)讨论当时,f(x)单调性.
(2)证明:.
22.已知平面上动点Q(x,y)到F(0,1)的距离比Q(x,y)到直线的距离小1,记动点Q(x,y)的轨迹为曲线C.
(1)求曲线C的方程.
(2)设点P的坐标为(0,-1),过点P作曲线C的切线,切点为A,若过点P的直线m与曲线C交于M,N两点,证明:.
参考答案:
1.B
【解析】
【分析】
先化简集合,再利用交集运算求解.
【详解】
因为,所以,即,所以.
故选:B.
2.D
【解析】
【分析】
根据已知条件求得的值,利用复数的乘法化简可得结果.
【详解】
因为复数的虚部与复数的虚部相等,则,则,
因此,.
故选:D.
3.A
【解析】
【分析】
根据数量积的运算求解即可
【详解】
故选:A
4.B
【解析】
【分析】
根据饼状图及有关数据得各个社团比例,计算人数及相应概率判断各选项.
【详解】
这五个社团的总人数为,.A错误,C错误.
因为太极拳社团人数的占比为,所以脱口秀社团人数的占比为
,B正确.从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为,D错误.
故选:B.
5.C
【解析】
【详解】
试题分析:时,成立,第一次进入循环:;成立,第二次进入循环:;成立,第三次进入循环:,不成立,输出,故选C.
【名师点睛】解决此类型问题时要注意:第一,要明确是当型循环结构,还是直到型循环结构,并根据各自的特点执行循环体;第二,要明确图中的累计变量,明确每一次执行循环体前和执行循环体后,变量的值发生的变化;第三,要明确循环体终止的条件是什么,会判断什么时候终止循环体,争取写出每一个循环,这样避免出错.
6.A
【解析】
【分析】
利用对数的运算及对数函数的性质进行比较大小.
【详解】
因为,所以;
因为,所以,
,,而,
所以,即.
故选:A.
7.C
【解析】
【分析】
根据给定条件,利用诱导公式、二倍角的余弦公式化简计算作答.
【详解】
依题意,,所以.
故选:C
8.C
【解析】
【分析】
作出平面区域,结合图像求直线在轴截距的最小值,通过平移直线可得在在点处取到最小值,代入运算求解.
【详解】
根据题意可得平面区域,如图所示:
∵目标函数,即,则求直线在轴截距的最小值
结合图像可得在点处取到最小值
故选:C.
9.B
【解析】
【分析】
圆心到直线的距离为,则,而,所以,解方程即可求出答案.
【详解】
圆的圆心,
所以圆心到直线的距离为,则,
而,所以,解得:.
故选:B.
10.C
【解析】
【分析】
根据给定条件,求出的关系式,再求出函数含有数0的单调区间即可判断作答.
【详解】
因直线是曲线的一条对称轴,则,即,
由得,则函数在上单调递增,
而函数在区间上不单调,则,解得,
所以的最小值为11.
故选:C
11.D
【解析】
【分析】
由是定义为R上的奇函数可知函数关于点对称;再结合,即可得出.再结合f(x)在上单调递增,在上单调递减,可知函数在上单调递减,在上单调递增,在上单调递减.再分类讨论即可你求出答案.
【详解】
因为是定义为R上的奇函数,
所以;函数关于点对称.
当时:;
当时:;
所以在上单调递减,在上单调递增,在上单调递减.
所以当时,解得;
当时,解得;
当时,解得;
综上所述:不等式的解集
故选:D.
12.B
【解析】
【分析】
利用双曲线的光学性质及双曲线定义,用表示,再在两个直角三角形中借助勾股定理求解作答.
【详解】
依题意,直线都过点,如图,有,,
设,则,显然有,,
,因此,,在,,
即,解得,即,令双曲线半焦距为c,在中,,即,解得,
所以E的离心率为.
故选:B
【点睛】
方法点睛:求双曲线离心率的三种方法:①定义法,通过已知条件列出方程组,求得得值,根据离心率的定义求解离心率;
②齐次式法,由已知条件得出关于的二元齐次方程,然后转化为关于的一元二次方程求解;
③特殊值法:通过取特殊值或特殊位置,求出离心率.
13.33
【解析】
【分析】
根据给定条件,利用等差数列性质求出首项和公差,再利用前n项公式计算作答.
【详解】
等差数列中,,由得,则公差,
首项,
所以.
故答案为:33
14.
【解析】
【分析】
求导,再根据导数的几何意义即可得出答案.
【详解】
解:由函数,
得,,
则,
故,
所以在点处的切线方程为,
即.
故答案为:.
15.1
【解析】
【分析】
利用椭圆的定义知,利用基本不等式即可求出的最小值.
【详解】
因为是椭圆的左、右焦点,P在椭圆上运动,
所以.
所以,所以(当且仅当时等号成立).
所以.
即的最小值为1.
故答案为:1
16.①③
【解析】
【分析】
由线面垂直的性质定理得线线垂直判断①,由正方体的性质,可通过到的距离来计算到的距离,从而判断②,根据棱锥体积公式,判断③,想象在不同位置时外接球的半径的变化,判断④.
【详解】
易证平面,平面,所以恒有,直线DE与直线AC所成角为90°,所以①是真命题.点E到直线AB的距离与点E到直线的距离有关,所以②是假命题.因为,由线面平行的判定定理可得平面,故点E到平面的距离d为定值,则为定值,所以③是真命题.平面,在上变化,例如点E在处和在的中点处时,三棱锥的外接球半径不同,故其外接球的体积不是定值,所以④是假命题.
故答案为:①③
17.(1)
(2)
【解析】
【分析】
(1)根据正弦定理结合内角的范围求解即可;
(2)由余弦定理与面积公式求解即可
(1)
由已知及正弦定理知:.
因为C为锐角,则,所以.
因为A为锐角,则
(2)
由余弦定理,.
则,即
即,因为,则
所以△ABC的面积.
18.(1)证明见解析,(2)
【解析】
【分析】
(1)由已知得an+12(an),,从而能证明{an}是首项为,公比为2的等比数列,并能求出{an}的通项公式.
(2)利用分组求和可求解
【详解】
(1)由可得,即
所以是一个以2为首项,以2为公比的等比数列
所以,所以
(2)
【点睛】
本题考查等比数列的证明,考查等比数列的通项公式及前n项和的求法,是中档题,解题时要认真审题,注意分组求和的合理运用.
19.(1)填表见解析;有97.5%的把握认为“对冰球是否有兴趣与性别有关”;
(2).
【解析】
【分析】
(1)根据给定数据,完善列联表,计算的观测值,再与临界值表比对作答.
(3)对5人编号,利用列举法结合古典概型概率公式计算作答.
(1)
根据已知数据得到如下列联表:
| 有兴趣 | 没有兴趣 | 台计 |
男 | 90 | 20 | 110 |
女 | 60 | 30 | 90 |
合计 | 150 | 50 | 200 |
根据列联表中的数据,得,,
所以有97.5%的把握认为“对冰球是否有兴趣与性别有关”.
(2)
记至少1人对冰球有兴趣为事件D
记5人中对冰球有兴趣的3人为A、B、C,对冰球没有兴趣的2人为m、n,
则从这5人中随机抽取2人,有,共10个结果,
其中2人对冰球都有兴趣的有,共3个结果,
1人对冰球有兴趣的有,共6个结果,则至少1人对冰球有兴趣的有9个结果,
所以所求事件的概率.
20.(1)证明见解析;
(2).
【解析】
【分析】
(1)证明,利用线面垂直判定定理求解;
(2)利用等体积法求点C到平面POM的距离即可.
(1)
连接OB,如图,
∵,∴,即△ABC是直角三角形,
又O为AC的中点,∴,又∵,
∴
∴.
∴,OB、AC平面ABC
∴PO⊥平面ABC.
(2)
由(1)得PO⊥平面ABC,
在中,,
.
设点C到平面POM的距离为d,由,
解得,
∴点C到平面POM的距离为.
21.(1)见解析;(2)证明见解析.
【解析】
【分析】
(1)对函数求导,按和两类讨论,得出函数的单调性;
(2)要证,即证.构造函数,利用函数的导数判断函数的单调性,求出函数的最小值,转化求解即可.
【详解】
(1)解:由题意可知
对于二次函数.
当时,恒成立,f(x)在上单调递减;
当时,二次函数有2个大于零的零点,分别是,
当,f(x)在单调递增;
当,f(x)在和单调递减
综上:当时,f(x)在(0,+∞)单调递减
当时f(x)在单调递增;单调递减.
(2)证明:要证,即证.
(方法一)设,则,在(0,+∞)上为增函数,
因为,所以在(,1)上存在唯一的零点m,
且,即.
所以h(x)在(0,m)上单调递减,在上单调递增,
所以,.
因为,所以等号不成立,所,
所以,从而原不等式得证
(方法二)不妨设,则,
当时,,当时,,
因此恒成立,.
则恒成立,.
则恒成立,即.
又,所以等号不成立,即,从而不等式得证
22.(1);
(2)证明见解析.
【解析】
【分析】
(1)由题意列出方程化简求解即可;
(2)要使,只需,利用斜率公式及根与系数的关系化简即可得证.
(1)
Q(x,y),由题意,得,
当时,,平方可得,
当时,,平方可得,
由可知,不合题意,舍去.
综上可得,所以Q的轨迹方程C为.
(2)
不妨设,因为,所以,
从而直线PA的斜率为,解得,即A(2,1),
又F(0,1),所以轴.要使,只需.
设直线m的方程为,代入并整理,得.
首先,,解得或.
其次,设,则,
,故.
此时直线m的斜率的取值范围为.
广西壮族自治区柳州市2024届新高三摸底考试数学试题(图片版含答案): 这是一份广西壮族自治区柳州市2024届新高三摸底考试数学试题(图片版含答案),文件包含柳州市2024届新高三摸底考数学试卷pdf、柳州市2024届新高三摸底考数学-答案+评分标准pdf等2份试卷配套教学资源,其中试卷共7页, 欢迎下载使用。
2023届广西柳州市高三第三次模拟数学(文)试题含解析: 这是一份2023届广西柳州市高三第三次模拟数学(文)试题含解析,共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
广西柳州市2023届新高三理数摸底考试试卷及答案: 这是一份广西柳州市2023届新高三理数摸底考试试卷及答案,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












