华师大版八年级上册第14章 勾股定理综合与测试单元测试课后复习题

华师大版初中数学八年级上册第十四章《勾股定理》单元测试卷 

考试范围：第十四章；考试时间：120分钟；总分120分

学校:___________姓名：___________班级：___________考号：___________

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、选择题（本大题共12小题，共36.0分）

1. 下列条件中，使不是直角三角形的是(    )

A. ，， B.
C.  D. ：：：：

2. 如图，在中，，为的中点，为上一点，过点作，交的延长线于点，若，，则四边形周长的最小值是(    )

A.  B.  C.  D.

3. 如图，在数轴上点，点表示的数分别为，，，，以点为圆心，长为半径画弧，交数轴于点，则点表示的数是(    )

A.  B.  C.  D.

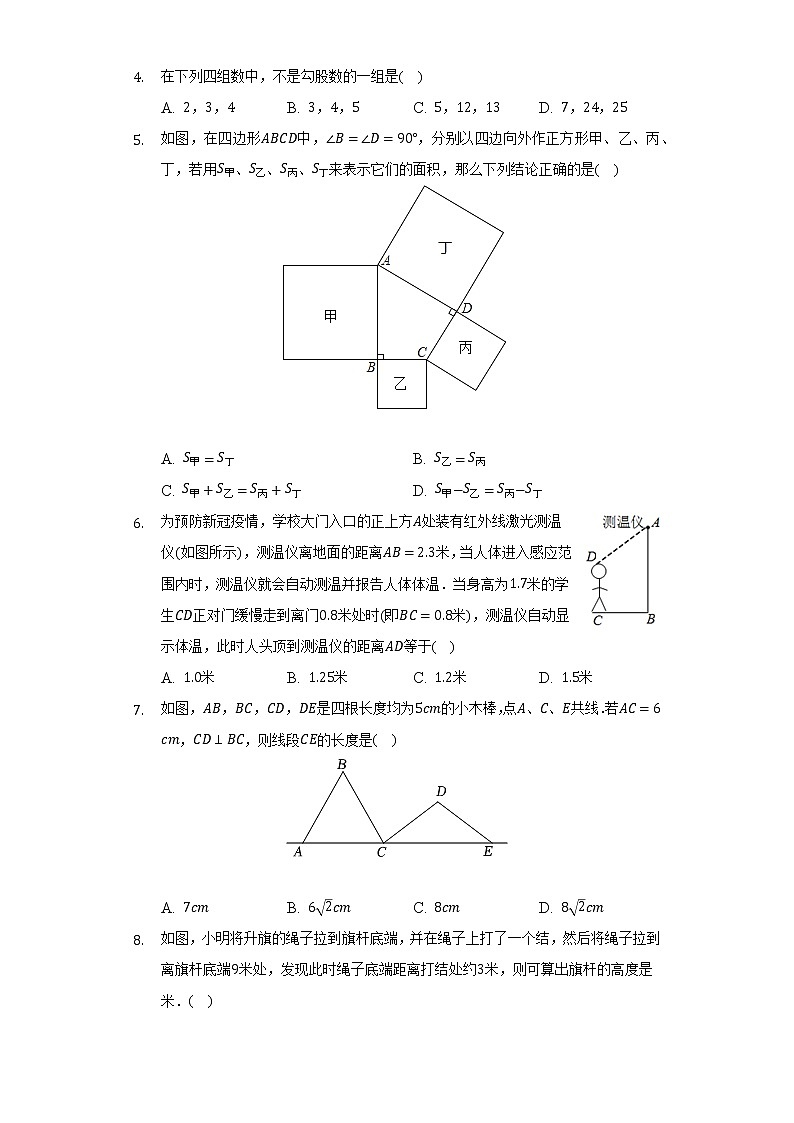
4. 在下列四组数中，不是勾股数的一组是(    )

A. ，， B. ，， C. ，， D. ，，

5. 如图，在四边形中，，分别以四边向外作正方形甲、乙、丙、丁，若用、、、来表示它们的面积，那么下列结论正确的是(    )

A.  B.
C.  D.

6. 为预防新冠疫情，学校大门入口的正上方处装有红外线激光测温仪如图所示，测温仪离地面的距离米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温．当身高为米的学生正对门缓慢走到离门米处时即米，测温仪自动显示体温，此时人头顶到测温仪的距离等于(    )

A. 米 B. 米 C. 米 D. 米

7. 如图，，，，是四根长度均为的小木棒，点、、共线．若，，则线段的长度是(    )

A.  B.  C.  D.

8. 如图，小明将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端米处，发现此时绳子底端距离打结处约米，则可算出旗杆的高度是米．(    )

A.  B.  C.  D.

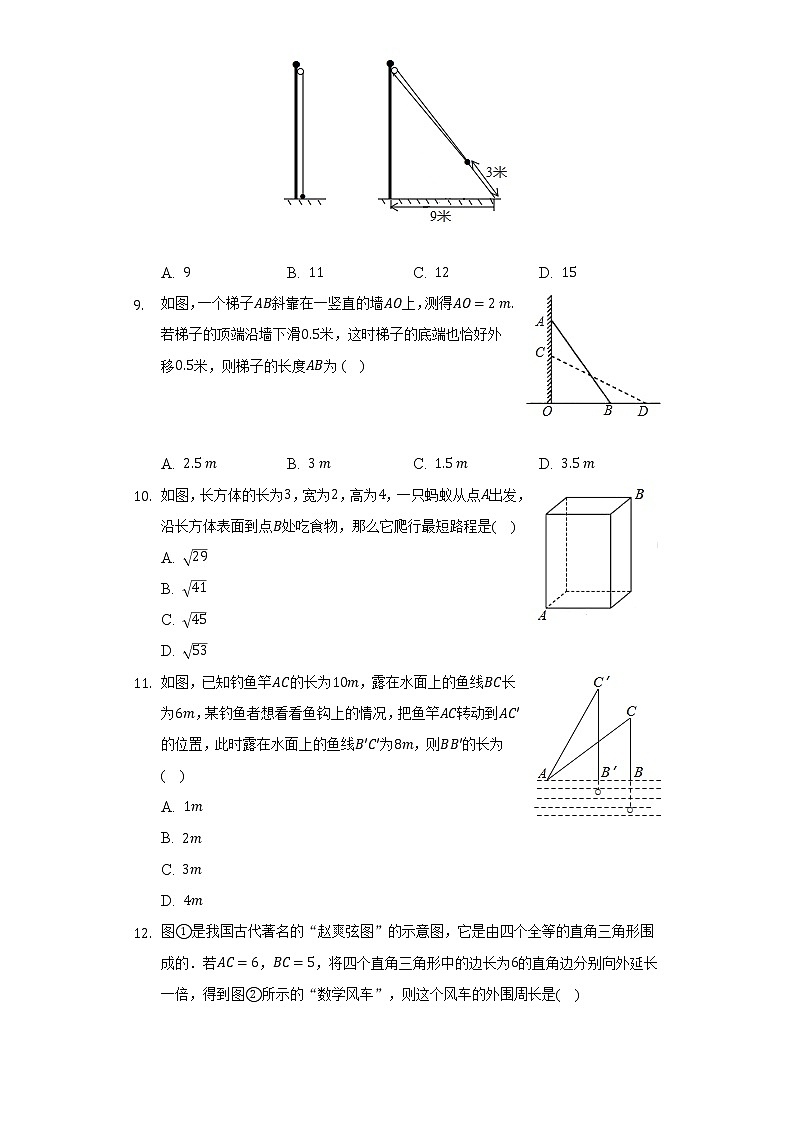
9. 如图，一个梯子斜靠在一竖直的墙上，测得若梯子的顶端沿墙下滑米，这时梯子的底端也恰好外移米，则梯子的长度为(    )

A.  B.  C.  D.

10. 如图，长方体的长为，宽为，高为，一只蚂蚁从点出发，沿长方体表面到点处吃食物，那么它爬行最短路程是(    )

A.
B.
C.
D.

11. 如图，已知钓鱼竿的长为，露在水面上的鱼线长为，某钓鱼者想看看鱼钩上的情况，把鱼竿转动到的位置，此时露在水面上的鱼线为，则的长为(    )

A.
B.
C.
D.

12. 图是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若，，将四个直角三角形中的边长为的直角边分别向外延长一倍，得到图所示的“数学风车”，则这个风车的外围周长是(    )

A.  B.  C.  D. 无法确定

第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）

13. 我国三国时期数学家赵爽为了证明勾股定理，创造了一幅“弦图”，后人称其为“赵爽弦图”，如图所示．在图中，若正方形的边长为，正方形的边长为，且，则正方形的边长为______．

14. 在中，，，高，则的周长是          ．
15. 一架云梯长米，如图斜靠在一面墙上，梯子的底端离墙米，如果梯子的顶端下滑了米，那么梯子的底端在水平方向滑动了______米．

16. 如图，，，是四根长度均为的火柴棒，其中，，点，，共线．若，则线段的长度是______．

三、解答题（本大题共9小题，共72.0分）

17. 如图所示，在每个小正方形的边长均为的方格纸中，有线段，点、均在小正方形的顶点上．
    
    在图中，画，使，点在小正方形的顶点上；
    在图中，画出以为边，面积为的和，点、在小正方形的顶点上，且和不全等．
18. 如图，在的网格中，每个小正方形的边长都为，的三个顶点都在格点上．
    ______，______；
    仅用无刻度的直尺作出边上的高保留作图痕迹

19. 如图．和都是等腰直角三角形，，，的顶点在的斜边上．
    求证：．

20. 如图，在中，．
    在边上求作一点，使到边的距离等于的长；要求：尺规作图，不写作法，保留作图痕迹
    在的条件下，若，，求的长．

21. 一梯子长，如图那样斜靠在一面墙上，梯子底端离墙．
    这架梯子的顶端离地面有多高？
    设梯子顶端到水平地面的距离为，底端到垂直墙面的距离为，若，根据经验可知：当时，梯子最稳定，使用时最安全．若梯子的顶端下滑了，请问这时使用是否安全．

22. “儿童散学归来早，忙趁东风放纸鸢”，又到了放风筝的最佳时节．某校八年级某班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度，他们进行了如下操作：
    测得水平距离的长为米；
    根据手中剩余线的长度计算出风筝线的长为米；
    牵线放风筝的小明的身高为米．
    求风筝的垂直高度；
    如果小明想风筝沿方向下降米，则他应该往回收线多少米？

23. 如图，某港口位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行海里和海里，小时后两船分别位于点，处，且相距海里，已知甲船沿北偏西方向航行，求乙船航行的方向．

24. 九章算术是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架，其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”其大意是：一根竹子高丈，折断后竹子顶端落在离竹子底端尺处．折断处离地面的高度是多少？其中丈、尺是长度单位，丈尺．

25. 城市绿化是城市重要的基础设施，是城市现代化建设的重要内容，是改善生态环境和提高广大人民群众生活质量的公益事业．某小区在社区管理人员及社区居民的共同努力之下，在临街的拐角清理出了一块可以绿化的空地，如图，，，．
    
    技术人员在只有卷尺的情况下，通过测量某两点之间距离，便快速确定了请写出技术人员测量的是哪两点之间的距离以及确定的依据；
    现计划在空地内种草，若每平方米草地造价元，这块地全部种草的费用是多少元？
    

答案和解析

1.【答案】 

【解析】解：、由，，得，符合勾股定理的逆定理，故是直角三角形；
B、由：：：：，符合勾股定理的逆定理，故是直角三角形；
C、符合勾股定理的逆定理，故是直角三角形；
D、由：：：：，及得，故不是直角三角形．
故选：．
依据勾股定理的逆定理，三角形内角和定理以及直角三角形的性质，即可得到结论．
本题考查了直角三角形的判定及勾股定理的逆定理，掌握直角三角形的判定及勾股定理的逆定理是解题的关键．
 

2.【答案】 

【解析】解：，
，
是的中点，
，
在和中，
，
≌，
，，
，，
四边形的周长，
当最小时，即时四边形的周长有最小值，
，，
，
四边形为矩形，
，
四边形的周长最小值为，
故选：．
通过证明≌可得，可得四边形的周长即为，进而可确定当时，四边形的周长有最小值，通过证明四边形为矩形可得的长，进而可求解．
本题主要考查全等三角形的判定与性质，确定的值是解题的关键．
 

3.【答案】 

【解析】解：在中，，，
由勾股定理得，，
，
则点表示的数为，
故选：．
根据题意运用勾股定理求出的长，即可得到答案．
本题考查的是勾股定理，实数与数轴的关系，正确运用勾股定理求出的长是解题的关键，要理解数轴上的点与实数的对应关系．
 

4.【答案】 

【解析】解：、，
，，不是一组勾股数，本选项符合题意；
B、，
，，，是一组勾股数，本选项不符合题意；
C、，
，，是一组勾股数，本选项不符合题意；
D、，
，，是一组勾股数，本选项不符合题意；
故选：．
根据勾股数的概念判断即可．
本题考查的是勾股数，满足的三个正整数，称为勾股数．
 

5.【答案】 

【解析】解：连接，
由勾股定理得，，
甲的面积乙的面积丙的面积丁的面积，
故选：．
连接，根据勾股定理可得甲的面积乙的面积丙的面积丁的面积，依此即可求解．
本题考查了勾股定理的知识，要求能够运用勾股定理证明个正方形的面积之间的关系．
 

6.【答案】 

【解析】解：如图，过点作于点，

米，米，米，
米．
在中，由勾股定理得到：米，
故选：．
过点作于点，构造，利用勾股定理求得的长度即可．
本题考查了勾股定理的应用，解题的关键是作出辅助线，构造直角三角形，利用勾股定理求得线段的长度．
 

7.【答案】 

【解析】解：由题意知，，，
过作于，过作于，
则，，，
，
，
，
，
在和中，
，
≌，
，
在中，
，，
，
，
，
故选：．
过作于，过作于，由等腰三角形的性质得到，，根据全等三角形判定证得≌，得到，在中，根据勾股定理求出，进而求出．
本题主要考查了等腰三角形的性质和判定，等腰三角形的性质，勾股定理，正确作出辅助线，证得≌是解决问题的关键．
 

8.【答案】 

【解析】解：设旗杆的高度为米，依题意得：
，
解得：；
故选：．
设旗杆的高度为米，由勾股定理得出方程，解方程即可．
本题考查了勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，从题意中勾画出勾股定理这一数学模型是解决问题的关键．
 

9.【答案】 

【解析】

【分析】
本题考查了勾股定理在实际生活中的应用，本题中找到为等量关系是解题的关键．
设，利用勾股定理用表示出和的长，进而求出的值，即可求出的长度．
【解答】
解：设，依题意，得，，．
在中，根据勾股定理得
，
在中，根据勾股定理
，
，
解得，
，即，
故梯子的长为，
故选A．  

10.【答案】 

【解析】解：第一种情况：把我们所看到的前面和上面组成一个平面，

则这个长方形的长和宽分别是和，
则所走的最短线段是；
第二种情况：把我们看到的左面与上面组成一个长方形，

则这个长方形的长和宽分别是和，
所以走的最短线段是；
第三种情况：把我们所看到的前面和右面组成一个长方形，

则这个长方形的长和宽分别是和，
所以走的最短线段是；
三种情况比较而言，第二种情况最短．
所以它需要爬行的最短路线的长是，
故选：．
作此题要把这个长方体中，蚂蚁所走的路线放到一个平面内，在平面内线段最短，根据勾股定理即可计算．
本题考查的是平面展开最短路径问题，熟知此类问题应先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．
 

11.【答案】 

【解析】解：，，
，
，，
，
；
故选：．
根据勾股定理分别求出和，再根据即可得出答案．
此题考查了勾股定理的应用，用到的知识点是勾股定理，根据已知条件求出和是解题的关键．
 

12.【答案】 

【解析】

【分析】
本题主要考查勾股定理的应用及识图能力．通过勾股定理可将“数学风车”的斜边求出，然后可求出风车外围的周长．
【解答】
解：依题意，设“数学风车”中的四个直角三角形的斜边长为，则，
所以．
所以“数学风车”的周长是．
故选C．  

13.【答案】 

【解析】解：


，


，
．
答：正方形的边长为．
故答案为：．
根据正方形面积公式，由面积的和差关系可得个直角三角形的面积，进一步得到个直角三角形的面积，再由面积的和差关系可得正方形的面积，进一步求出正方形的边长．
考查了勾股定理的证明，关键是熟练掌握正方形面积公式，以及面积的和差关系，难点是得到正方形的面积．
 

14.【答案】或 

【解析】解：此题应分两种情况说明：
如图，当为锐角三角形时，
在中， ，
在中， ，，
，
的周长为
如图，当为钝角三角形时，
同理，在中， ，
在中，，
．
的周长为．
综上所述，的周长是或．

15.【答案】 

【解析】

【分析】
本题考查了勾股定理在实际生活中的运用，考查了直角三角形中勾股定理的运用，本题中正确的使用勾股定理是解题的关键．先利用勾股定理可以得出梯子的顶端距离地面的高度，得出梯子的初始高度，下滑米后，可得出梯子的顶端距离地面的高度，已知梯子的底端距离墙的距离为米，再次使用勾股定理，可以得出梯子底端水平方向上滑行的距离．
【解答】
解：设梯子的底端在水平方向滑动了米，
根据勾股定理得：
梯子距离地面的高度为：；
又梯子下滑了米，
即梯子距离地面的高度为，
根据勾股定理：
，
解得：或舍去．
即梯子的底端在水平方向滑动了米，
故答案为：．  

16.【答案】 

【解析】解：作，，垂足分别为、，
，
，
，
，
，
，
在和中，
，
≌，
，
，，，
，
，
在中，
由勾股定理得：，
，
，，
，
，
故答案为：．
作，，垂足分别为、，利用证明≌得到，利用勾股定理及等腰三角形的性质求出，再根据等腰三角形的性质即可得出答案．
本题主要考查了等腰三角形的性质，勾股定理，正确作出辅助线，证得≌是解决问题的关键．
 

17.【答案】解：如图，即为所求；
如图，，即为所求．
 

【解析】根据要求作出图形即可；
根据要求作出图形即可．
本题考查作图应用与设计作图三角形的面积等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
 

18.【答案】  

【解析】解：，；
故答案为：，．
如图，线段即为所求．

利用勾股定理求解即可；
取格点，连接交于点，线段即为所求．
本题考查作图应用与设计作图，勾股定理等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
 

19.【答案】证明：连接，

和都是等腰直角三角形，，，
，，
，
即，
在和中，
，
≌，
，，
，
，
． 

【解析】连接，结合等腰直角三角形的性质利用证明≌可得，，再利用勾股定理可证明结论．
本题主要考查等腰直角三角形，全等三角形的判定与性质，勾股定理，证明≌是解题的关键．
 

20.【答案】解：如图，点即为所求；


过点作于点．
，，，
，
平分，，，
，
，
． 

【解析】作的角平分线交于点即可；
利用勾股定理求出，再利用面积法求出．
本题考查作图复杂作图，角平分线的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
 

21.【答案】解：由题意可知，，，，
，
答：这架梯子的顶端离地面有高；
这时使用不安全，理由如下：
由题意得：，
在中，，，
，
，
这时使用不安全． 

【解析】由勾股定理求出的长即可；
由题意得：，再由勾股定理得，则，即可得出结论．
本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．
 

22.【答案】解：在中，
由勾股定理得，，
所以，负值舍去，
所以，米，
答：风筝的高度为米；
设风筝从点下降到点，连接，

由题意得，米，
米，
米，
，
他应该往回收线米． 

【解析】利用勾股定理求出的长，再加上的长度，即可求出的高度；
根据勾股定理即可得到结论．
本题考查了勾股定理的应用，熟悉勾股定理，能从实际问题中抽象出勾股定理是解题的关键．
 

23.【答案】解：由题意可知：，，，
，
是直角三角形，
，
由题意知，
，
即乙船沿北偏东方向航行． 

【解析】根据题意即可知，，，利用勾股定理的逆定理可推出是直角三角形，由甲船沿北偏西方向航行，即可推出乙船的航行方位角．
本题考查勾股定理的应用以及方位角，熟练掌握勾股定理并能熟练应用以及能正确找出方位角是解题的关键．
 

24.【答案】解：设折断处离地面尺，
根据题意可得：，
解得：．
答：折断处离地面尺． 

【解析】根据题意结合勾股定理得出折断处离地面的高度即可．
此题主要考查了勾股定理的应用，根据题意正确应用勾股定理是解题关键．
 

25.【答案】解：测量的是点，之间的距离；
依据是：如果是三角形的三边长，，满足，那么这个三角形是直角三角形；
连接，
由得，
在中，，
在中，，，
，
，
，
平方米，
元，
答：这块地全部种草的费用是元． 

【解析】根据勾股定理的逆定理即可得到结论；
连接，根据勾股定理和勾股定理的逆定理即可得到结论．
此题考查了勾股定理，以及勾股定理的逆定理，熟练掌握定理及逆定理是解本题的关键．