
河南省南阳市卧龙区2021—2022学年七年级下学期期末调研测试数学试题(word版含答案)
展开2021-2022学年河南省南阳市卧龙区七年级(下)期末数学试卷
一、选择题。(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.(3分)已知等式3m=2n+5,则下列等式变形不正确的是( )
A.3m+1=2n+6 B.3m﹣5=2n C.6m=4n+5 D.m=
2.(3分)数学中的对称之美无处不在,下列四幅常见的垃圾分类标志图案(不考虑文字说明)中,既是轴对称图形又是中心对称图形的是( )
A.有害垃圾 B.可回收物
C.厨余垃圾 D.其他垃圾
3.(3分)如果a<b,那么下列各式中错误的是( )
A.3+a<3+b B.3﹣a<3﹣b C.3a<3b D.<
4.(3分)下面三根小木棒能摆成三角形的是( )
A.5cm,5cm,11cm B.3cm,4cm,5cm
C.8cm,7cm,15cm D.13cm,2cm,20cm
5.(3分)不等式的解集是( )
A.x>﹣4 B.x<﹣4 C.x>﹣6 D.x<﹣6
6.(3分)现有几种形状的正多边形地砖,分别是:①正三角形:②正方形;③正五边形:④正六边形,每一种正多边形地砖的大小形状都相同,且都有很多块,如果只用其中的一种正多边形地砖镶嵌,那么不能够镶嵌成一个平面图案的正多边形是( )
A.① B.② C.③ D.④
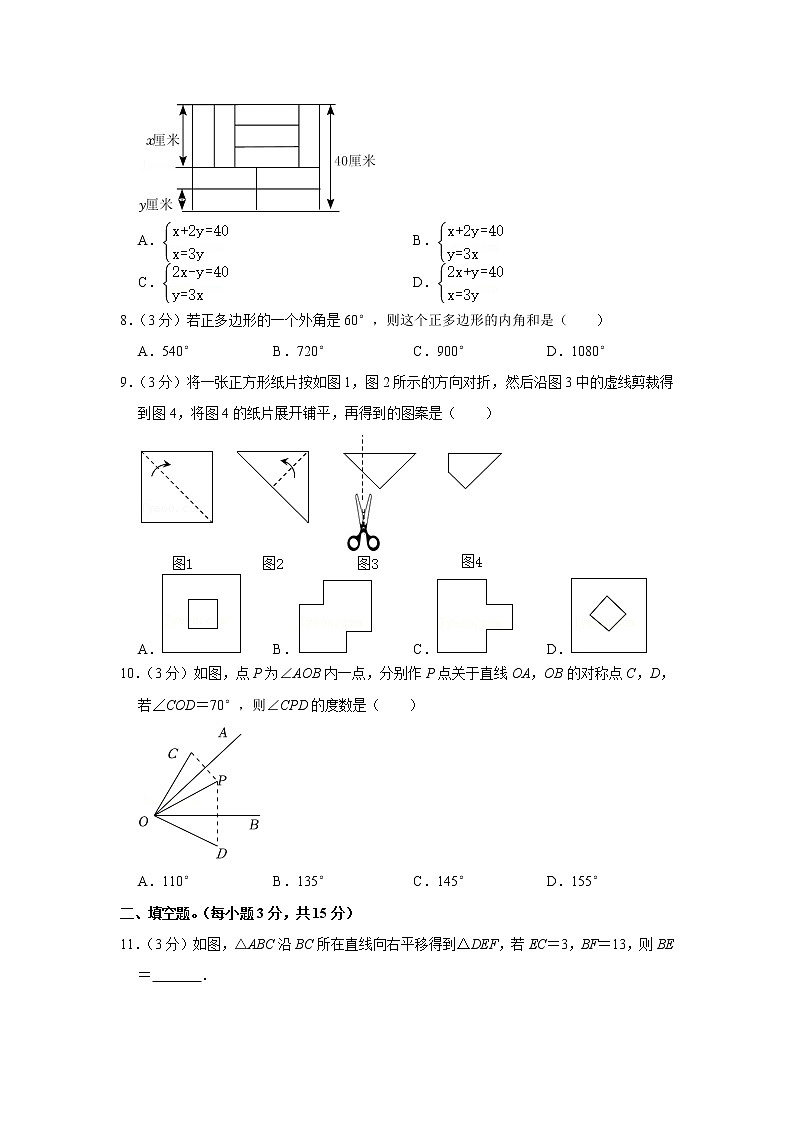
7.(3分)如图,10块形状、大小相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意可列方程组为( )
A. B.
C. D.
8.(3分)若正多边形的一个外角是60°,则这个正多边形的内角和是( )
A.540° B.720° C.900° D.1080°
9.(3分)将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是( )
A. B. C. D.
10.(3分)如图,点P为∠AOB内一点,分别作P点关于直线OA,OB的对称点C,D,若∠COD=70°,则∠CPD的度数是( )
A.110° B.135° C.145° D.155°
二、填空题。(每小题3分,共15分)
11.(3分)如图,△ABC沿BC所在直线向右平移得到△DEF,若EC=3,BF=13,则BE= .
12.(3分)已知x,y满足方程组,则x+y的值为 .
13.(3分)如图,由一个正六边形和一个正五边形组成的图形中∠1的度数是 .
14.(3分)如图,已知△ABC,直线a⊥AC于点D,且AD=CD,点P是直线a上一动点,连接PB,PC,若AB=5,AC=6,BC=3,则△PBC周长的最小值是 .
15.(3分)如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为 .
三、解答题。(共75分)
16.(8分)解方程组:.
17.(9分)解不等式组,并求出该不等式组的最小整数解.
18.(9分)如图,在方格纸内将△ABC水平向右平移4个单位得到△A'B'C'.
(1)补全△A'B'C',利用网格点和直尺画图;
(2)图中AC与A'C'的关系是: ;
(3)画出△ABC中AB边上的中线CD与高CE;
(4)平移过程中,线段AC扫过的面积是 .
19.(9分)如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.连接AD,试说明DA+DB+DC与的大小关系.
20.(8分)如图,在△ABC中,∠B=25°,∠BAC=31°,过点A作BC边上的高,交BC的延长线于点D,CE平分∠ACD,交AD于点E.求∠AEC的度数.
21.(10分)如图,在△ABC中,∠C=90°,点M,N分别在边AB,BC上,且点A,B关于直线MN对称,连接AN.
(1)若∠CAN=α,则∠B与α之间的数最关系为 ;
(2)若,,且△ABC的周长为24.求△ACN的周长.
22.(11分)为了让学生加强体育锻炼,增强体质,2022版新课标中,体育与健康的课时占比将提高到10%~11%.某学校提前适应这一变化,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不超过260元,若要求购买跳绳的数量多于20根.
①求共有哪几种购买方案;
②比较哪一种购买方案更省钱.
23.(11分)小新是七年级的学生,他用的数学教材是华师大版,学习过程中,在做完七年级下册第82页习题4后,老师经过思考,对该习题进行了下面的变式,让同学们解决,也请你解决下面的问题.
如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,外角∠MBC,∠NCB的平分线交于点Q,延长线段BP,QC交于点E.
(1)如果∠A=64°,求∠BPC的度数;
(2)探索∠Q与∠A之间的数量关系;
(3)若在△BQE中,存在一个内角等于另一个内角的3倍,请直接写出锐角∠A的度数.
2021-2022学年河南省南阳市卧龙区七年级(下)期末数学试卷
参考答案与试题解析
一、选择题。(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.(3分)已知等式3m=2n+5,则下列等式变形不正确的是( )
A.3m+1=2n+6 B.3m﹣5=2n C.6m=4n+5 D.m=
【分析】根据等式的基本性质,逐一进行计算即可判断.
【解答】解:A、∵3m=2n+5,
∴3m+1=2n+6,
故A不符合题意;
B、∵3m=2n+5,
∴3m﹣5=2n,
故B不符合题意;
C、∵3m=2n+5,
∴6m=4n+10,
故C符合题意;
D、∵3m=2n+5,
∴m=,
故D不符合题意;
故选:C.
【点评】本题考查了等式的性质,熟练掌握等式的基本性质是解题的关键.
2.(3分)数学中的对称之美无处不在,下列四幅常见的垃圾分类标志图案(不考虑文字说明)中,既是轴对称图形又是中心对称图形的是( )
A.有害垃圾 B.可回收物
C.厨余垃圾 D.其他垃圾
【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
【解答】解:A.既是中心对称图形,也是轴对称图形,故此选项符合题意;
B.既不是中心对称图形,也不是轴对称图形,故此选项不合题意;
C.不是中心对称图形,是轴对称图形,故此选项不合题意;
D.不是中心对称图形,是轴对称图形,故此选项不合题意;
故选:A.
【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
3.(3分)如果a<b,那么下列各式中错误的是( )
A.3+a<3+b B.3﹣a<3﹣b C.3a<3b D.<
【分析】根据不等式的性质,可得答案.
【解答】解:A、∵a<b,
∴3+a<3+b,原变形正确,故此选项不符合题意;
B、∵a<b,
∴﹣a>﹣b,
∴3﹣a>3﹣b,原变形错误,故此选项符合题意;
C、∵a<b,
∴3a<3b,原变形正确,故此选项不符合题意;
D、∵a<b,
∴<,原变形正确,故此选项不符合题意.
故选:B.
【点评】本题考查了不等式的性质,熟知不等式的性质是解答此题的关键.
4.(3分)下面三根小木棒能摆成三角形的是( )
A.5cm,5cm,11cm B.3cm,4cm,5cm
C.8cm,7cm,15cm D.13cm,2cm,20cm
【分析】三角形的三条边必须满足:任意两边之和>第三边,任意两边之差<第三边.
【解答】解:A、5+5<11,不能组成三角形,不符合题意;
B、3+4>5,能组成三角形,符合题意;
C、8+7=15,不能组成三角形,不符合题意;
D、13+2<20,不能组成三角形,不符合题意.
故选:B.
【点评】本题主要考查对三角形三边关系的理解应用.判断是否可以构成三角形,只要判断两个较小的数的和>最大的数就可以.
5.(3分)不等式的解集是( )
A.x>﹣4 B.x<﹣4 C.x>﹣6 D.x<﹣6
【分析】利用不等式的基本性质,移项、合并同类项以及化系数为1即可求得原不等式的解集.
【解答】解:,
去分母,得x+5>﹣2x﹣7,
移项,得3x>﹣12,
解得x>﹣4.
故选:A.
【点评】本题考查了一元一次不等式,熟练掌握一元一次不等式的解法是解题的关键.
6.(3分)现有几种形状的正多边形地砖,分别是:①正三角形:②正方形;③正五边形:④正六边形,每一种正多边形地砖的大小形状都相同,且都有很多块,如果只用其中的一种正多边形地砖镶嵌,那么不能够镶嵌成一个平面图案的正多边形是( )
A.① B.② C.③ D.④
【分析】根据判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能判断即可.
【解答】解:①正三角形的每个内角是60°,60°×6=360°,能镶嵌,故①不符合题意;
②正方形的每个内角是90°,90°×4=360°,能镶嵌,故②不符合题意;
③正五边形的每个内角是108°,不能镶嵌,故③符合题意;
④正六边形的每个内角是120°,120°×3=360°,能镶嵌,故④不符合题意;
故选:C.
【点评】本题考查了平面镶嵌(密铺),掌握判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能是解题的关键.
7.(3分)如图,10块形状、大小相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意可列方程组为( )
A. B.
C. D.
【分析】根据图示可得:矩形的宽可以表示为(x+2y)厘米,宽又是40厘米,故x+2y=40,矩的长可以表示为2x,或x+3y,故2x=3y+x,整理得x=3y,联立两个方程即可.
【解答】解:根据图示可得:.
故选:A.
【点评】此题主要考查了由实际问题抽象出二元一次方程组,关键是看懂图示,分别表示出长方形的长和宽.
8.(3分)若正多边形的一个外角是60°,则这个正多边形的内角和是( )
A.540° B.720° C.900° D.1080°
【分析】根据多边形的边数与多边形的外角的个数相等,可求出该正多边形的边数,再由多边形的内角和公式求出其内角和.
【解答】解:该正多边形的边数为:360°÷60°=6,
该正多边形的内角和为:(6﹣2)×180°=720°.
故选:B.
【点评】本题考查多边形的内角与外角,解答本题的关键是求出该正多边形的边数与熟记多边形的内角和公式.
9.(3分)将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是( )
A. B. C. D.
【分析】对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.
【解答】解:严格按照图中的顺序向右上翻折,向左上角翻折,剪去左上角,展开得到结论.
故选:B.
【点评】本题考查的是剪纸问题,此类题目主要考查学生的动手能力及空间想象能力,对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.
10.(3分)如图,点P为∠AOB内一点,分别作P点关于直线OA,OB的对称点C,D,若∠COD=70°,则∠CPD的度数是( )
A.110° B.135° C.145° D.155°
【分析】根据对称的性质得出∠C+∠D=∠CPD,再根据四边形内角和是360°得出∠CPD的度数,即可得出结论.
【解答】解:根据对称知,∠C=∠OPC,∠D=∠OPD,
∵∠COD=70°,
∴∠C+∠D=∠CPD=(360°﹣70°)=145°,
故选:C.
【点评】本题主要考查对称的性质,四边形的内角和等知识,熟练掌握对称的知识及四边形内角和是360°是解题的关键.
二、填空题。(每小题3分,共15分)
11.(3分)如图,△ABC沿BC所在直线向右平移得到△DEF,若EC=3,BF=13,则BE= 5 .
【分析】根据平移的性质得到EF=BC,进而得到BE=CF,计算即可.
【解答】解:由平移的性质可知,EF=BC,
∴EF﹣EC=BC﹣EC,即BE=CF,
∵EC=3,BF=13,
∴BE+CF=10,
∴BE=5,
故答案为:5.
【点评】本题考查的是平移的性质,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
12.(3分)已知x,y满足方程组,则x+y的值为 ﹣2 .
【分析】用加减消元法解二元一次方程组,然后求解.
【解答】解:方法一:,
①﹣②,得:2x+2y=﹣4,
∴x+y=﹣2,
故答案为:﹣2.
方法二:,
②×2,得:4x+2y=6③,
①﹣③,得:y=﹣7,
把y=﹣7代入②,得2x﹣7=3,
解得:x=5,
∴方程组的解为,
∴x+y=﹣2,
故答案为:﹣2.
【点评】本题考查解二元一次方程组,掌握消元法解方程组的步骤,利用整体思想解题是关键.
13.(3分)如图,由一个正六边形和一个正五边形组成的图形中∠1的度数是 84° .
【分析】利用正多边形的外角公式可得∠3,∠4,再根据三角形内角和为180°,求出∠2,即可求出∠1解决问题.
【解答】解:如图,
由题意得:∠3=360°÷6=60°,∠4=360°÷5=72°,
则∠2=180°﹣60°﹣72°=48°,
所以∠1=360°﹣48°﹣120°﹣108°=84°
故答案为84°.
【点评】本题考查多边形内角与外角,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
14.(3分)如图,已知△ABC,直线a⊥AC于点D,且AD=CD,点P是直线a上一动点,连接PB,PC,若AB=5,AC=6,BC=3,则△PBC周长的最小值是 8 .
【分析】找出C点关于a的对称点A,AB交a于P,则△PBC的周长最小,求出即可.
【解答】解:设直线a与AB交于P′,当点P与点P′重合时,PB+PC最小,即△PBC的周长最小,
∵直线a⊥AC于点D,且AD=CD,
∴直线a是AC的垂直平分线,
∴P′C=P′A,
∴△PBC的周长=PC+PB+BC=P′A+P′B+BC=AB+BC=5+3=8,
∴△PBC周长的最小值是8,
故答案为:8.
【点评】本题主要考查轴对称﹣最短路线问题,确定P点的位置是解答本题的关键.
15.(3分)如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为 15°,45°,105°,135°,150° .
【分析】要分5种情况进行讨论:AD∥BC、DE∥AB、DE∥BC、DE∥AC、AE∥BC分别画出图形,再分别计算出度数即可.
【解答】解:当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的情况如下图所示:
①当AD∥BC时,α=15°;②当DE∥AB时,α=45°;③当DE∥BC时,α=105°;④当DE∥AC时,α=135°;⑤当AE∥BC时,α=150°.
故答案为:15°,45°,105°,135°,150°.
【点评】本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
三、解答题。(共75分)
16.(8分)解方程组:.
【分析】由①得出x+5y=0③,②+③得出3x=﹣6,求出x,再把x=﹣2代入③求出y即可.
【解答】解:,
由①,得x+5y=0③,
②+③,得3x=﹣6,
解得:x=﹣2,
把x=﹣2代入③,得﹣2+5y=0,
解得:,
所以原方程组的解是.
【点评】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.
17.(9分)解不等式组,并求出该不等式组的最小整数解.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式①,得:x>﹣,
解不等式②,得:x≤4,
则不等式组的解集为﹣<x≤4,
∴不等式组的最小整数解为﹣2.
【点评】本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
18.(9分)如图,在方格纸内将△ABC水平向右平移4个单位得到△A'B'C'.
(1)补全△A'B'C',利用网格点和直尺画图;
(2)图中AC与A'C'的关系是: AC∥A′C′,AC=A′C′ ;
(3)画出△ABC中AB边上的中线CD与高CE;
(4)平移过程中,线段AC扫过的面积是 28 .
【分析】(1)利用平移变换的性质分别作出A,B,C 对应点A′,B′,C′即可;
(2)利用平移变换的性质判断即可;
(3)根据三角形的中线,高的定义画出图形即可;
(4)利用平行四边形的面积公式求解.
【解答】解:(1)如图,△A′B′C′即为所求;
(2)AC∥A′C′,AC=A′C′.
故答案为:AC∥A′C′,AC=A′C′;
(3)如图,线段CD,CE即为所求;
(4)线段AC扫过的面积=4×7=28,
故答案为:28.
【点评】本题考查作图﹣平移变换,三角形的中线,高,平行四边形的面积等知识,解题的关键是掌握平移变换性质,属于中考常考题型.
19.(9分)如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.连接AD,试说明DA+DB+DC与的大小关系.
【分析】由三角形的三边关系得:DA+DB>AB,DB+DC>BC,DA+DC>AC,则2(DA+DB+DC)>AB+BC+AC,即可得出结论.
【解答】解:DA+DB+DC>,
理由:在△ABD中,AD+BD>AB.
在△BCD中,BD+CD>BC.
在△ACD中,AD+CD>AC.
∴AD+BD+BD+CD+AD+CD>AB+BC+AC.
∴.
【点评】本题考查了三角形的三边关系以及角平分线的定义等知识;熟练掌握三角形的三边关系是解题的关键.
20.(8分)如图,在△ABC中,∠B=25°,∠BAC=31°,过点A作BC边上的高,交BC的延长线于点D,CE平分∠ACD,交AD于点E.求∠AEC的度数.
【分析】求出∠ECD,∠D,利用三角形的外角的性质求解即可.
【解答】解:∵∠ACD=∠B+∠BAC,∠B=25°,∠BAC=31°,
∴∠ACD=25°+31°=56°.
∵AD⊥BD,
∴∠D=90°,
∵∠ACD=56°,CE平分∠ACD,
∴∠ECD=∠ACD=28°,
∴∠AEC=∠ECD+∠D=28°+90°=118°.
【点评】本题考查三角形内角和定理,三角形外角的性质,角平分线的定义等知识,解题关键是熟知基础知识能根据图形选择合适的性质进行角的计算和转化.
21.(10分)如图,在△ABC中,∠C=90°,点M,N分别在边AB,BC上,且点A,B关于直线MN对称,连接AN.
(1)若∠CAN=α,则∠B与α之间的数最关系为 α+2∠B=90° ;
(2)若,,且△ABC的周长为24.求△ACN的周长.
【分析】(1)由∠C=90°,可得α+∠NAB+∠B=90°,根据点A,B关于直线MN对称,即得α+2∠B=90°;
(2)由△ABC的周长为24,,,可得AC=6,即可得△ACN的周长=AC+CN+AN=AC+BC=14.
【解答】解:(1)∵∠C=90°,
∴∠CAB+∠B=90°,即α+∠NAB+∠B=90°,
∵点A,B关于直线MN对称,
∴∠NAB=∠B,
∴α+2∠B=90°;
故答案为:α+2∠B=90°;
(2)∵△ABC的周长为24,
∴AC+BC+AB=24,
∵,,
∴,
解得AC=6,
∴BC=8,AB=10,
∵点A,B关于直线MN对称,
∴AN=BN,
∴△ACN的周长
=AC+CN+AN
=AC+CN+BN
=AC+BC
=6+8=14.
【点评】本题考查轴对称的性质,三角形内角和定理等知识,解题的关键是利用NA=BN解决问题,属于中考常考题型.
22.(11分)为了让学生加强体育锻炼,增强体质,2022版新课标中,体育与健康的课时占比将提高到10%~11%.某学校提前适应这一变化,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不超过260元,若要求购买跳绳的数量多于20根.
①求共有哪几种购买方案;
②比较哪一种购买方案更省钱.
【分析】(1)根据“购买2根跳绳和5个毽子共需32元,购买4根跳绳和3个毽子共需36元”列出相应的二元一次方程组,计算即可;
(2)①根据“购买跳绳和毽子的总数量是54,且购买的总费用不超过260元”列出相应的一元一次不等式,计算即可;
②将上述购买方式所需的钱计算比较即可.
【解答】解:(1)设购买一根跳绳需要x元,购买一个毽子需要y元,根据题意得:
,、
解得,
答:购买一根跳绳需要6元,购买﹣一个毽子需要4元;
(2)①设购买m根跳绳,则购买(54﹣m)个毽子,根据题意得:
6m+4(54﹣m)≤260,
解得:m≤22,
由题意知m>20,∴20<m≤22.
又∵m为正整数,∴m可以为21,22.
∴共有下面2种购买方案:
方案1:购买21根跳绳,33个毽子;
方案2:购买22根跳绳,32个毽子;
②方案1的购买费用为:21×6+33×4=258.
方案2的购买费用为:22×6+32×4=260.258<260,
答:方案1的购买费用更省钱.
【点评】本题考查了一元一次不等式,二元一次方程组,根据题干信息列出方程组或不等式是解题的关键.
23.(11分)小新是七年级的学生,他用的数学教材是华师大版,学习过程中,在做完七年级下册第82页习题4后,老师经过思考,对该习题进行了下面的变式,让同学们解决,也请你解决下面的问题.
如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,外角∠MBC,∠NCB的平分线交于点Q,延长线段BP,QC交于点E.
(1)如果∠A=64°,求∠BPC的度数;
(2)探索∠Q与∠A之间的数量关系;
(3)若在△BQE中,存在一个内角等于另一个内角的3倍,请直接写出锐角∠A的度数.
【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠ABC+∠ACB,进而求出∠BPC即可解决问题;
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;
(3)在△BQE中,由于∠Q=90°﹣∠A,求出∠E=∠A,∠EBQ=90°,所以如果△BQE中,存在一个内角等于另一个内角的3倍,那么分四种情况进行讨论:①∠EBQ=3∠E=90°;②∠EBQ=3∠Q=90°;③∠Q=3∠E;④∠E=3∠Q;分别列出方程,求解即可.
【解答】解:(1)∵∠A=64°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣64°=116°,
∵∠ABC与∠ACB的平分线交于点P,
∴,,
∴=;
(2)∵外角∠MBC,∠NCB的平分线交于点Q,
∴,.
∴==;
(3)如图,延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的3倍,那么分四种情况:
①∠EBQ=3∠E=90°,则∠E=30°,∠A=2∠E=60°;
②∠EBQ=3∠Q=90°,则∠Q=30°,∠E=60°,∠A=2∠E=120°;
③∠Q=3∠E,则∠E=22.5°,解得∠A=45°;
④∠E=3∠Q,则∠E=67.5°,解得∠A=135°.
综上所述,∠A的度数是60°或120°或45°或135°.
【点评】本题是三角形综合题,考查了三角形内角和定理、外角的性质,角平分线定义等知识;灵活运用三角形的内角和定理、外角的性质进行分类讨论是解题的关键.
河南省南阳市卧龙区2022-2023学年七年级下学期期末考试数学试题(含答案): 这是一份河南省南阳市卧龙区2022-2023学年七年级下学期期末考试数学试题(含答案),文件包含七年级数学docx、七年级数学答案docx等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
河南省南阳市卧龙区2021-2022年七年级下学期期末数学试题: 这是一份河南省南阳市卧龙区2021-2022年七年级下学期期末数学试题
2021-2022学年河南省南阳市卧龙区七年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年河南省南阳市卧龙区七年级(下)期末数学试卷(Word解析版),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












