
数学选择性必修 第一册第三章 圆锥曲线的方程3.1 椭圆教案设计
展开课题:3.1.1椭圆及其标准方程(第1课时)教学设计
一.教材及学情分析:
《椭圆及其标准方程》是北师大版选修2-1第三章第一节的内容,是学生学习了直线和圆等有关知识后学习的第二种圆锥曲线,本节课既是对前面所学知识情况进行检查,又为后面进一步学习双曲线与抛物线打好基础,所以学好本节课内容具有承上启下的重要意义.
根据本节内容的特点,教学过程中可充分发挥信息技术深度融合教学的作用,用视频动画、几何画板的动态作图等开发学生的数学思维,有助于学生进一步学习本课。教学过程注意体现数学思想方法及价值,如:数形结合思想、化归思想等,培养学生的数学核心素养。
二.教学目标
(一)知识与技能:
(1)掌握椭圆的定义;
(2)理解椭圆标准方程的推导过程,掌握椭圆标准方程的两种形式,会运用定义法以及待定系数法求椭圆的标准方程。
(二)过程与方法:
(1)经历从徒手画椭圆以及几何画板演示椭圆的形成过程,再类比圆的形成及定义抽象出椭圆模型,并进一步形成椭圆的定义,逐步提高学生的观察、分析、归纳、类比、概括能力;
(2)通过椭圆标准方程的推导,进一步掌握求曲线方程的一般方法——坐标法,并渗透数形结合、等价转化的数学思想方法。
(三)情感、态度与价值观:
(1)通过实践性、探究性、微视频学习,提高学生学习数学的兴趣;
(2)通过观察、合作探究等活动,培养团结合作、实事求是的风貌。
三.教学重点与难点
重点:椭圆的定义和椭圆标准方程的两种形式,理解几何问题代数化的数学思想
难点:椭圆的标准方程的建立、推导、化简以及坐标法的运用
四.教法建议
(1)通过类比圆到椭圆的形成过程中蕴含着运动变化的思想,由学生通过观察、猜想,从而使学生参与知识的获取、抽象、归纳的全过程,得到了椭圆的定义及其应注意条件,提高学生的综合分析能力.
(2)微视频演示椭圆方程的推导过程,充分调动学生自主学习,并从中体会数学知识的和谐美和获取知识的喜悦,体现微时代下多渠道及多方位获取知识。
(3)将课堂还给学生,培养学生团结协作的团队精神,展现学生为主,教师为辅的课改教学。
五.教学过程
学生徒手画椭圆,“定性”认识椭圆 → 视频演示直观认识椭圆 →
类比圆归纳形成椭圆定义 → 观看微视频用坐标法“定量”地描述椭圆 → 得出椭圆标准方程→ 实例演练加深理解 → 合作交流、巩固所学 →学生总结、完成思维导图
教学 环节 | 教学程序及设计 | 设计意图 |
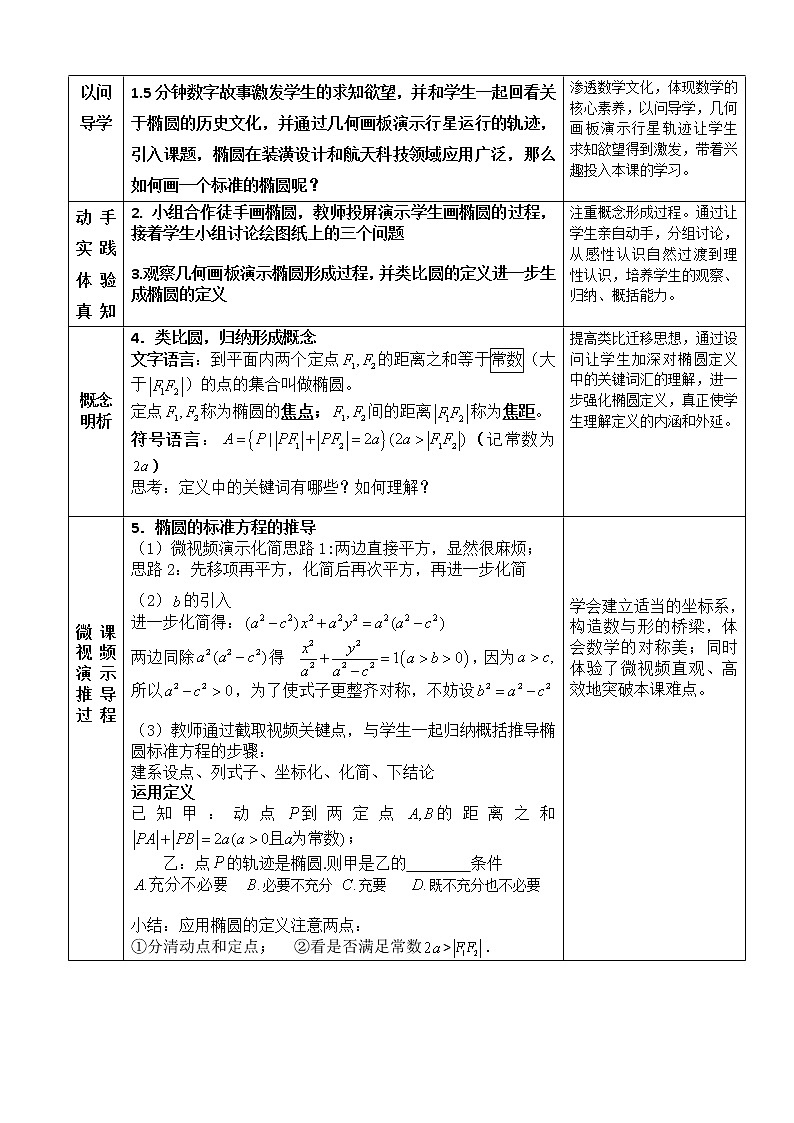
以问导学 | 1.5分钟数字故事激发学生的求知欲望,并和学生一起回看关于椭圆的历史文化,并通过几何画板演示行星运行的轨迹,引入课题,椭圆在装潢设计和航天科技领域应用广泛,那么如何画一个标准的椭圆呢? | 渗透数学文化,体现数学的核心素养,以问导学,几何画板演示行星轨迹让学生求知欲望得到激发,带着兴趣投入本课的学习。 |
动手实 践 体验真 知 |
3.观察几何画板演示椭圆形成过程,并类比圆的定义进一步生成椭圆的定义 | 注重概念形成过程。通过让学生亲自动手,分组讨论,从感性认识自然过渡到理性认识,培养学生的观察、归纳、概括能力。 |
概念明析
| 4.类比圆,归纳形成概念 文字语言:到平面内两个定点的距离之和等于常数(大于)的点的集合叫做椭圆。 定点称为椭圆的焦点;间的距离称为焦距。 符号语言:(记常数为) 思考:定义中的关键词有哪些?如何理解?
| 提高类比迁移思想,通过设问让学生加深对椭圆定义中的关键词汇的理解,进一步强化椭圆定义,真正使学生理解定义的内涵和外延。 |
微课视频演 示 推导过 程
| 5.椭圆的标准方程的推导 (1)微视频演示化简思路1:两边直接平方,显然很麻烦; 思路2:先移项再平方,化简后再次平方,再进一步化简 (2)的引入 进一步化简得: 两边同除得,因为 所以,为了使式子更整齐对称,不妨设
(3)教师通过截取视频关键点,与学生一起归纳概括推导椭圆标准方程的步骤: 建系设点、列式子、坐标化、化简、下结论 运用定义 已知甲:动点到两定点的距离之和; 乙:点的轨迹是椭圆.则甲是乙的 条件 充分不必要 必要不充分 充要 既不充分也不必要
小结:应用椭圆的定义注意两点: ①分清动点和定点; ②看是否满足常数>. |
学会建立适当的坐标系,构造数与形的桥梁,体会数学的对称美;同时体验了微视频直观、高效地突破本课难点。
|
微课视频演 示 推 导过 程 | (4)焦点在轴上椭圆的标准方程: 焦点在轴上椭圆的标准方程: 注:椭圆的标准方程为专有名词,为以上两种形式。 (5)椭圆标准方程的特点: (等号右侧为1,左侧“+”号相连;分子为,且系数为1;分母谁大,焦点落谁上;且满足)
|
微视频推导过程中为学生准备思考的问题,并给学生预留思考时间。
体现对称的思想及数学的美感。学生运用类比的方法,大胆猜想出方程。对学生观察、归纳能力的训练。 |
学以致 用 | 【用中学】了解椭圆方程的特点后,通过一个找椭圆的游戏加深对椭圆方程特点的理解,对找到的椭圆方程再进一步判断椭圆的焦点在哪条轴上,指出,写出焦点坐标. ① ② ③
总结反思: |
以游戏活跃课堂氛围,提高学生求知欲望,强化理解,深化知识点的掌握,突出重点、难点 。
|
学 以致 用
学 以致 用
|
【例中学】 已知椭圆两个焦点的坐标分别为,并且经过点,求椭圆的标准方程. (一)学生合作探究,整合课前预习书写的过程,教师巡视,学生可能会呈现多种解法,学生上台分享解决方法 思路1:利用椭圆定义(椭圆上的点到两个焦点、的距离之和为常数2)求出值,再结合已知条件和、、间的关系求出的值,进而写出标准方程; 思路2:先根据已知条件设出焦点在轴上的椭圆方程的标准方程,再将椭圆上点的坐标代入此方程,并结合、、间的关系求出、的值,从而得到椭圆的标准方程为 思路3:数形结合,为直角三角形,由勾股定理易求得,再同思路2,易求出标准方程 若将改为呢? 总结反思: (二)求解椭圆方程常用方法:定义法、待定系数法 (三)求椭圆方程的步骤: (1)一定焦点位置 (2)二设椭圆方程 (3)三求 (4)四写标准方程 如果你是出题者,你会如何改编此题?
|
多角度、多方法解决问题,开拓学生的思维,训练学生思维的严谨性。掌握数学的内涵与外延,体现了一题多解的数学思维。
以例代练,充分让学生动手、动脑。及时反馈,强化知识点的学习,也起到激发学生学习数学的兴趣的作用。
学生自主编题,发散学生的数学思维。 |
思维导图 总结反思 | 总结方式多角度: ①以表格形式回顾本课所学知识; ②以押韵诗句“椭圆方程有特点,系数为正加相连,分母较大焦点定,右边数1记心间”便于学生记住方程的特点; ③思维导图有助记忆持久 以红包形式呈现课后作业: ①完成课后三练 ②完善思维导图 ③汇编错题好题
| 摆脱传统教学中教师小结的做法,表格式、诗句式、思维导图式多角度总结让学生记忆更持久。 |
板书设计
| 椭圆的标准方程
焦点在轴上: 焦点在轴上: 方法总结:
| |
五.教学反思
本节课以问题为纽带,以探究活动为载体,通过实践、探索、体验、反思等活动把探究活动层层展开、步步深入,亲身经历知识的产生过程。使学生在知识的形成过程中,获得数学的情感体验,享受到成功的乐趣,同时在思想方法运用、思维能力等方面得到提高和发展。学生在生生互动、师生互动中把学生的学习过程转变为学生观察问题、发现问题、分析问题、解决问题的过程,希望对学生的思维品质的培养、数学思想的建立、心理品质的优化起到良好的作用。本节课由教师的引导,计算机辅助软件的融入,学生的学三方有效结合的把控仍有些欠缺,仍需调整,争取融合得更好。
人教A版 (2019)选择性必修 第一册3.1 椭圆优质课第一课时教学设计: 这是一份人教A版 (2019)选择性必修 第一册3.1 椭圆优质课第一课时教学设计,共8页。
高中人教A版 (2019)3.1 椭圆教案: 这是一份高中人教A版 (2019)3.1 椭圆教案,共10页。教案主要包含了探究新知,典例解析,小结,课时练等内容,欢迎下载使用。
数学选择性必修 第一册第三章 圆锥曲线的方程3.1 椭圆教学设计及反思: 这是一份数学选择性必修 第一册第三章 圆锥曲线的方程3.1 椭圆教学设计及反思,共10页。教案主要包含了探究新知,典例解析,小结,课时练等内容,欢迎下载使用。













