2021-2022学年北京市朝阳区陈经纶中学分校七年级（下）期中数学试卷（含解析）

2021-2022学年北京市朝阳区陈经纶中学分校七年级（下）期中数学试卷

一．选择题（本题共8小题，共16分）

1. 北京冬奥会吉祥物冰墩墩如图所示受到全世界人民喜爱．在下面右侧的四个图形中，能由如图经过平移得到的图形是

A.
B.
C.
D.
 

2. 下列说法错误的是

A. 的立方根是 B. 的平方根是
C. 的相反数是 D.

3. 下列命题中，假命题是

A. 对顶角相等
B. 同一平面内，过一点有且只有一条直线与已知直线垂直
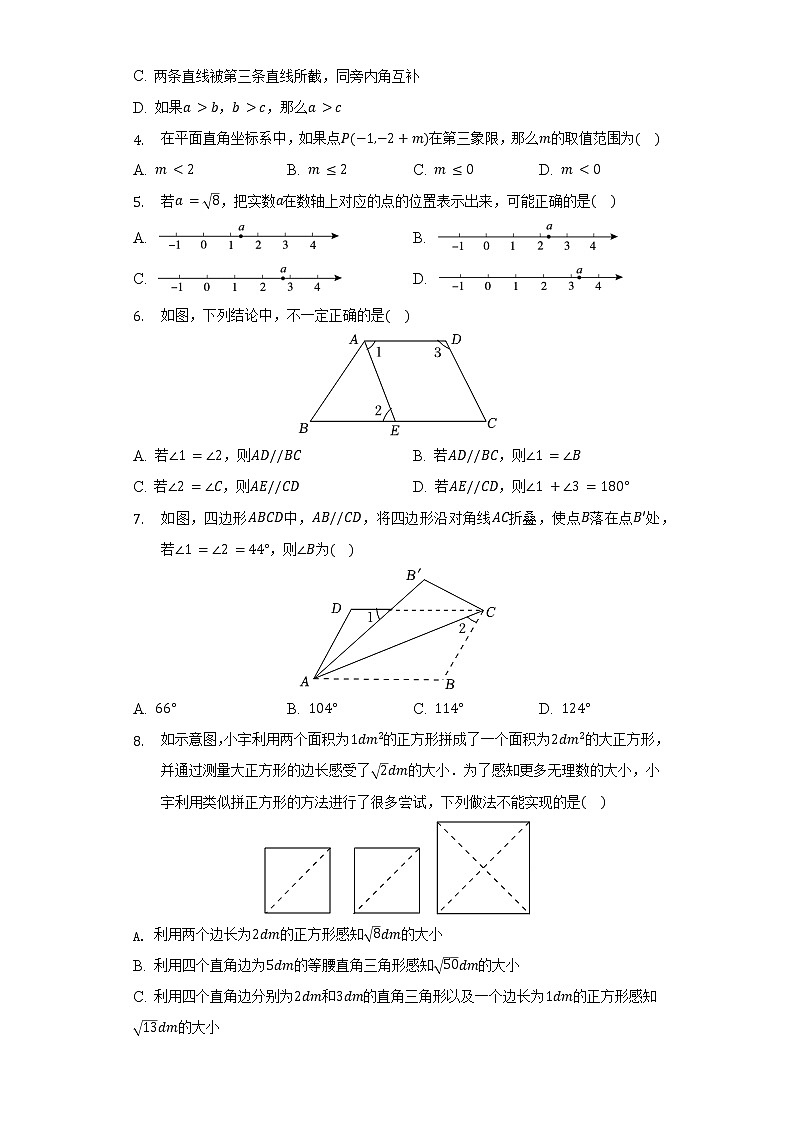
C. 两条直线被第三条直线所截，同旁内角互补
D. 如果，，那么

4. 在平面直角坐标系中，如果点在第三象限，那么的取值范围为

A.  B.  C.  D.

5. 若，把实数在数轴上对应的点的位置表示出来，可能正确的是

A.  B.
C.  D.

6. 如图，下列结论中，不一定正确的是

A. 若，则 B. 若，则
C. 若，则 D. 若，则

7. 如图，四边形中，，将四边形沿对角线折叠，使点落在点处，若，则为

A.  B.  C.  D.

8. 如示意图，小宇利用两个面积为的正方形拼成了一个面积为的大正方形，并通过测量大正方形的边长感受了的大小．为了感知更多无理数的大小，小宇利用类似拼正方形的方法进行了很多尝试，下列做法不能实现的是

1. 
   利用两个边长为的正方形感知的大小
   B. 利用四个直角边为的等腰直角三角形感知的大小
   C. 利用四个直角边分别为和的直角三角形以及一个边长为的正方形感知的大小
   D. 利用一个边长为的正方形以及一个直角边为的等腰直角三角形感知的大小

二．填空题（本题共8小题，共24分）

9. 已知方程，用含的代数式表示______．
10. 若，那么______．
11. 一把直尺和一个含，角的三角板如图所示摆放，直尺一边与三角板的两直角边分别交于，两点，另一边与三角板的两直角边分别交于，两点，且，那么的大小为______．
12. 已知是二元一次方程的一个解，则的值等于______．
13. 如图，一根细线上端固定，下端系一个小重物，让这个小重物来回自由摆动，来回摆动一次所用的时间单位：与细线长度单位：之间满足关系当细线的长度为时，小重物来回摆动一次所用的时间是______结果保留小数点后一位．
    
     

14. 在平面直角坐标系中，点，点坐标分别是，，在轴上求一点，使三角形的面积是，则点坐标是______．
15. 小明说永远不可能成立，因为在不等式两边都除以，得到这个错误结论，小明的说法______填“正确”或”不正确”．
    说明理由______．
16. 小李在五张同样的纸片上各写了一个正整数，从中随机抽取张，并将它们上面的数相加，重复这样做，每次所得的和都是，，，中的一个数，并且这四个数都能取到．猜猜看，小李在五张纸片上各写了什么数．满足条件的五个数有组，请写出一组满足条件的数______．

三．解答题（本题共11小题，共60分）

17. 计算：．
18. 解方程组：．
19. 解不等式，并把它的解集在数轴上表示出来．
20. 已知：及内部一点．
    过点作直线于点；
    过点作直线交于点；
    与的数量关系是______．
     

21. 能同时小于和的值吗？说明理由．
22. 完成下面的证明．
    如图，已知，，，为的平分线．
    求证：．
    证明：为的平分线
    ______角平分线定义
    
    ______
    ______
    又
    ______
    ______

23. 如图，已知三角形，是的平分线，平移三角形，使点移动到点，点的对应点是，点的对应点是．
    在图中画出平移后的三角形；
    若，与相交于点，则______，______

24. 为了迎接年北京冬奥会，某校开展“冰雪结缘”滑雪体验课程．先后两次在某商场购买滑雪护具和防护头盔，第一次买套滑雪护具和个防护头盔共花费元；第二次买套滑雪护具和个防护头盔共花费元．
    求每套滑雪护具和每个防护头盔各多少元？
    如果现在商场均以标价的折对滑雪护具和防护头盔进行促销，学校决定从该商场一次性购买滑雪护具和防护头盔共个，且总费用不能超过元，那么最多可以购买多少个防护头盔．
25. 阅读下列材料：
    解答“已知，且，，试确定的取值范围“有如下解法：
    解：因为，所以又因为，所以，所以．
    又，所以．
    同理得：
    由得，
    所以的取值范围是．
    请按照上述方法，完成下列问题：
    已知，且，，则的取值范围是______．
    已知关于，的方程组的解都为正数．
    求的取值范围；
    已知，求的取值范围．
26. 如图，对于平面直角坐标系中的任意两点，，它们之间的曼哈顿距离定义如下：已知为坐标原点，点，．
    
    ______ ， ______ ．
    已知点，其中为任意实数．
    若，求的值．
    若、、三点在曼哈顿距离下是等腰三角形，请直接写出的值．
27. 如图，，点，分别在直线，上，，过点作的延长线交于点，交于点，平分，交于点，交于点．
     

直接写出，，之间的关系：______．
若，求．
如图，在的条件下，将绕着点以每秒的速度逆时针旋转，旋转时间为，当边与射线重合时停止，则在旋转过程中，当的其中一边与的某一边平行时，直接写出此时的值．
答案和解析

1.【答案】

【解析】解：观察各选项图形可知，选项的图案可以通过平移得到．
故选：．
根据平移只改变图形的位置，不改变图形的形状与大小解答．
本题考查了生活中的平移现象，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．
 

2.【答案】

【解析】解：，故选项A正确；
的平方根是，故选项B正确；
与只有符号不同，它们互为相反数，故选项C正确；
，
，故选项D错误．
故选：．
利用平方根、立方根、相反数、绝对值的意义，逐个分析得结论．
本题考查了相反数、平方根、立方根及绝对值的化简，题目难度不大，掌握有理数的相关定义是解决本题的关键．
 

3.【答案】

【解析】解：、对顶角相等，本选项说法是真命题，不符合题意；
B、同一平面内，过一点有且只有一条直线与已知直线垂直，本选项说法是真命题，不符合题意；
C、两条平行线被第三条直线所截，同旁内角互补，故本选项说法是假命题，符合题意；
D、如果，，那么，本选项说法是真命题，不符合题意；
故选：．
根据对顶角相等、垂直的定义、平行线的性质、不等式的性质判断即可．
本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．掌握对顶角的性质、垂直的判断、平行线的性质、不等式的性质是解题的关键．
 

4.【答案】

【解析】解：由题意知，
则，
故选：．
根据解一元一次不等式基本步骤移项、合并同类项可得．
本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
 

5.【答案】

【解析】解：，
，
故选：．
利用夹值法求出的取值范围，即可选出答案．
本题主要考查了是实数在数轴上的表示，熟悉实数与数轴的关系是解答此题的关键．
 

6.【答案】

【解析】解：、，
，原结论正确，故此选项不符合题意；
B、，
，但无法得到与的关系，原结论不一定正确，故此选项符合题意；
C、，
，原结论正确，故此选项不符合题意；
D、，
，原结论正确，故此选项不符合题意；
故选：．
由平行线的性质和判定解答即可．
本题考查了平行线的判定与性质．熟练掌握平行线的判定与性质是解决问题的关键，注意它们之间的区别．
 

7.【答案】

【解析】解：，，
，
由折叠得，，
，
，
，
故选C．
由平行线得到，由折叠得到，由三角形的内角和求得的度数．
本题考查了平行线的性质，三角形的内角和定理，折叠的性质，解题的关键是利用平行线的性质求得．
 

8.【答案】

【解析】解：，，不符合题意；
B.，，不符合题意；
C.，，不符合题意；
D.，，但是一个边长为的正方形以及一个直角边为的等腰直角三角形无法得到边长为的正方形，符合题意．
故选：．
在拼图的过程中，拼前，拼后的面积相等，所以我们只需要分别计算拼前，拼后的面积，看是否相等，就可以逐个排除．
本题主要考查利用二次根式计算面积，解题的关键是在拼图的过程中，拼前，拼后的面积相等．
 

9.【答案】

【解析】解：方程，
解得：，
故答案为：
把看做已知数求出即可．
此题考查了解二元一次方程，解题的关键是将看做已知数求出．
 

10.【答案】或

【解析】解：，
或．
故答案为：或．
一个正数有两个平方根，这两个平方根互为相反数，据此求出的值即可．
此题主要考查了平方根的含义和求法，解答此题的关键是要明确：一个正数有两个平方根，这两个平方根互为相反数，零的平方根是零，负数没有平方根．
 

11.【答案】

【解析】解：，，
，
，
，
故答案为：．
先根据，，即可得到，最后根据，即可得出的大小．
本题主要考查了平行线的性质以及直角三角形的性质的运用，解题解题的关键是掌握平行线的性质：两直线平行，同位角相等．
 

12.【答案】

【解析】解：把代入二元一次方程，得，
，
．
故答案为．
根据方程的解的定义，把这对数值代入方程，那么得到一个含有未知数的一元一次方程，即可求得．
此题主要考查了二元一次方程组解的定义，理解定义是关键．
 

13.【答案】

【解析】解：把代入关系式得，
．
答：小重物来回摆动一次所用的时间大约是．
故答案为：．
直接把代入关系式即可求出的值．
此题考查的是二次根式的应用，熟练掌握算术平方根的定义是解题关键．
 

14.【答案】或

【解析】解：设点的坐标为，
点，点坐标分别是，，
，
三角形的面积是，
，
，
，
或，
点坐标是或，
故答案为：或．
设点的坐标为，根据点的坐标特征得到，然后利用三角形面积公式得到关于的方程，解方程即可．
本题考查了坐标与图形的性质，三角形的面积，表示出三角形的底和高是解题的关键．
 

15.【答案】不正确  当时，

【解析】解：小明的说法不正确．理由如下：
当时，；
当时，由得．
故答案是：不正确；当时，．
根据不等式的性质进行解答．
本题考查了不等式的性质：不等式两边加上或减去同一个数，不等号方向不变；不等式两边乘以或除以同一个正数，不等号方向不变；不等式两边乘以或除以同一个负数，不等号方向改变．
 

16.【答案】，，，

【解析】解：相加得的两个整数可能为：，或，或，．
相加得的两个整数可能为：，或，或，．
相加得的两个整数可能为：，或，或，或，．
相加得的两个整数可能为：，或，或，或，．
每次所得两个整数和最小是，
最小的数字可以为，
每次所得两个整数和最大是，
最大的数字可以为，
四个整数可以分别为，，，．
故答案为：，，，．
分别列出两数相加为，，，的所有可能性求解．
本题考查有理数的应用，解题关键是利用分类讨论求解．
 

17.【答案】解：原式

．

【解析】本题涉及开平方、开立方、绝对值等考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．
此题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握开平方、开立方、绝对值等考点的运算．
 

18.【答案】解：，
得，
，
解得，
将代入，得，
，
解得，
所以原方程的解为．

【解析】利用加减消元法即可解答．
本题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
 

19.【答案】解：，
，
．
把解集表示在数轴上为：
 

【解析】去括号、移项、合并同类项、系数化为．
此题考查一元一次不等式的解法及在数轴上表示不等式的解集，属基础题．
 

20.【答案】互余

【解析】解：如图，为所作；
如图，为所作；

，
，
，
，
．
故答案为互余．
根据几何语言画出对应的几何图形；
利用平行线的性质得到，再利用垂直的定义得到，从而得到．
本题考查了作图复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了平行线的性质．
 

21.【答案】解：能同时小于和的值，理由如下：
由得：，
．
由得：，
．
．
能同时小于和的值．

【解析】列不等式组求解．
本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
 

22.【答案】  两直线平行，内错角相等      同旁内角互补，两直线平行

【解析】证明：为的平分线，
角平分线定义，
，
两直线平行，内错角相等，
，
又，
，
同旁内角互补，两直线平行．
故答案为：；两直线平行，内错角相等；；；同旁内角互补，两直线平行．
由为的平分线，根据角平分线的定义可得：，然后由，根据两直线平行，内错角相等，可得，进而可得：，然后根据同旁内角互补，两直线平行，即可证明与平行．
此题考查了平行线的判定与性质，解题的关键是：熟记同位角相等两直线平行，内错角相等两直线平行，同旁内角互补两直线平行．
 

23.【答案】 

【解析】解：如图，即为所求；

是的平分线，
，
由平移的性质知，，，
，
，
故答案为：，．
根据平移的性质可画出；
利用平移的性质得，，再根据平行线的性质和三角形内角和定理可得答案．
本题主要考查了平移的性质，平行线的性质，三角形内角和定理等知识，利用平移的性质准确画出图形是解题的关键．
 

24.【答案】解：设每套滑雪护具元，每个防护头盔元，
根据题意，得：，
解得，
答：每套滑雪护具元，每个防护头盔元；
设可以购买个防护头盔，则滑雪护具需购买个，
根据题意，得：，
解得：，
是正整数，
，
答：最多可以购买个防护头盔．

【解析】设每套滑雪护具元，每个防护头盔元，根据“第一次买套滑雪护具和个防护头盔共花费元；第二次买套滑雪护具和个防护头盔共花费元”列二元一次方程组求解即可；
设可以购买个防护头盔，则滑雪护具需购买个，根据“总费用不能超过元”列出关于的一元一次不等式求解即可．
本题主要考查一元一次不等式和二元一次方程组的应用，解题的关键是根据题意找到其中蕴含的相等关系和不等关系．
 

25.【答案】

【解析】解：，
．
又，
．
．
又，
，
同理，可得，
，得．
故答案为：；
解方程组得，，
由题意知，
解得；
，
，
，
，
解得，
则．
仿照阅读材料求出的取值范围；
解出一元一次不等式组，仿照阅读材料求出的取值范围．
本题考查的是一元一次不等式和一元一次不等式组的解法，掌握一元一次不等式的解法、理解阅读材料是解题的关键．
 

26.【答案】 

【解析】解：由题意，，．
故答案为，．

由题意：，
当时，，
当时，，
综上所述，的值为或．

由题意，或或，
当时，，
解得或；
当时，，
解得或，
当时，，
解得，
综上所述，的值为或或或或．
根据曼哈顿距离的定义求解即可．
构建方程求解即可．
由题意，或或，分这个情况得到关于的方程，解方程即可．
本题考查了新定义，绝对值方程，分类讨论是解题的关键．
 

27.【答案】
，
，，
，
，
，
，
，
平分，
，
，
，
，
，
，
，
，
．
当时，延长交边于，

，
，
，
，
，
当绕点旋转时，，
秒，
当时，

，
，
，
，
当绕点旋转时，，
秒，
当时，即与在同一直线上时，

，
当绕点旋转时，，
秒，
当的其中一边与的某一边平行时的值为秒或秒或秒．
当时，

，
．
当旋转时，．
秒．
当时，

，，
．
当旋转时，．
秒．
当的其中一边与的某一边平行时的值为秒或秒或秒或秒或秒．

【解析】解：，
，
，
．
故答案为：；
见答案．
根据平行线的性质可得答案；
根据，分别表示出、、、、和，再由，可得的度数，则问题可解；
结合，分以下几种情况求解：当时，延长交边于，当时，当时，即与在同一直线上时，当时，当时．
本题考查了平行线的性质、三角形的内角和及一元一次方程在几何问题中的应用，理清题中的数量关系并分类讨论是解题的关键．