2021-2022学年北京十三中分校七年级（下）期中数学试卷（含解析）

2021-2022学年北京十三中分校七年级（下）期中数学试卷

一、选择题（本大题共10小题，共20分）

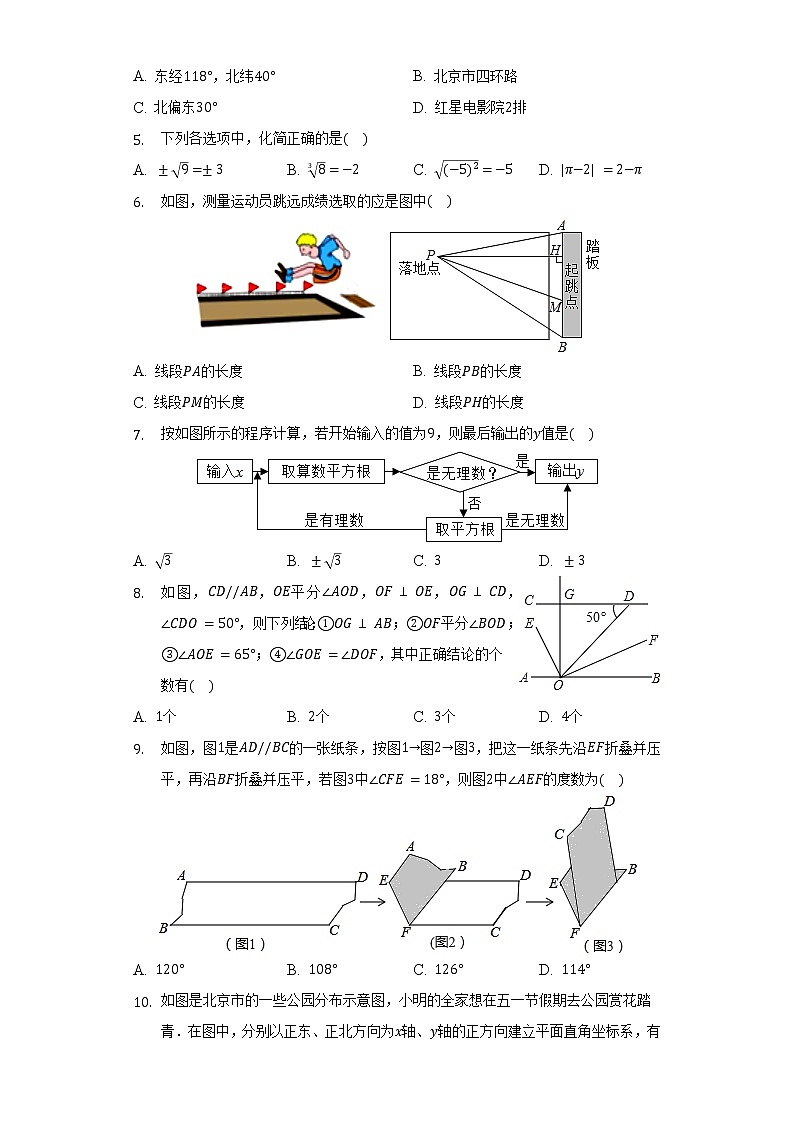
1. 北京年冬奥会会徽是以汉字“冬”为灵感来源设计的．在下面如图的四个图中，能由如图经过平移得到的是

A.
B.
C.
D.

2. 在实数、、、、、、、、不循环中，无理数的个数为

A. 个 B. 个 C. 个 D. 个

3. 下列命题是真命题的是

A. 和为的两个角是邻补角
B. 一条直线的垂线有且只有一条
C. 点到直线的距离是指这点到直线的垂线段
D. 两条直线被第三条直线所截，如内错角相等，则同位角必相等

4. 根据下列表述，能确定位置的是

A. 东经，北纬 B. 北京市四环路
C. 北偏东 D. 红星电影院排

5. 下列各选项中，化简正确的是

A.  B.  C.  D.

6. 如图，测量运动员跳远成绩选取的应是图中

A. 线段的长度 B. 线段的长度
C. 线段的长度 D. 线段的长度

7. 按如图所示的程序计算，若开始输入的值为，则最后输出的值是

A.  B.  C.  D.

8. 如图，，平分，，，，则下列结论：；平分；；，其中正确结论的个数有

A. 个 B. 个 C. 个 D. 个

9. 如图，图是的一张纸条，按图图图，把这一纸条先沿折叠并压平，再沿折叠并压平，若图中，则图中的度数为

A.  B.  C.  D.

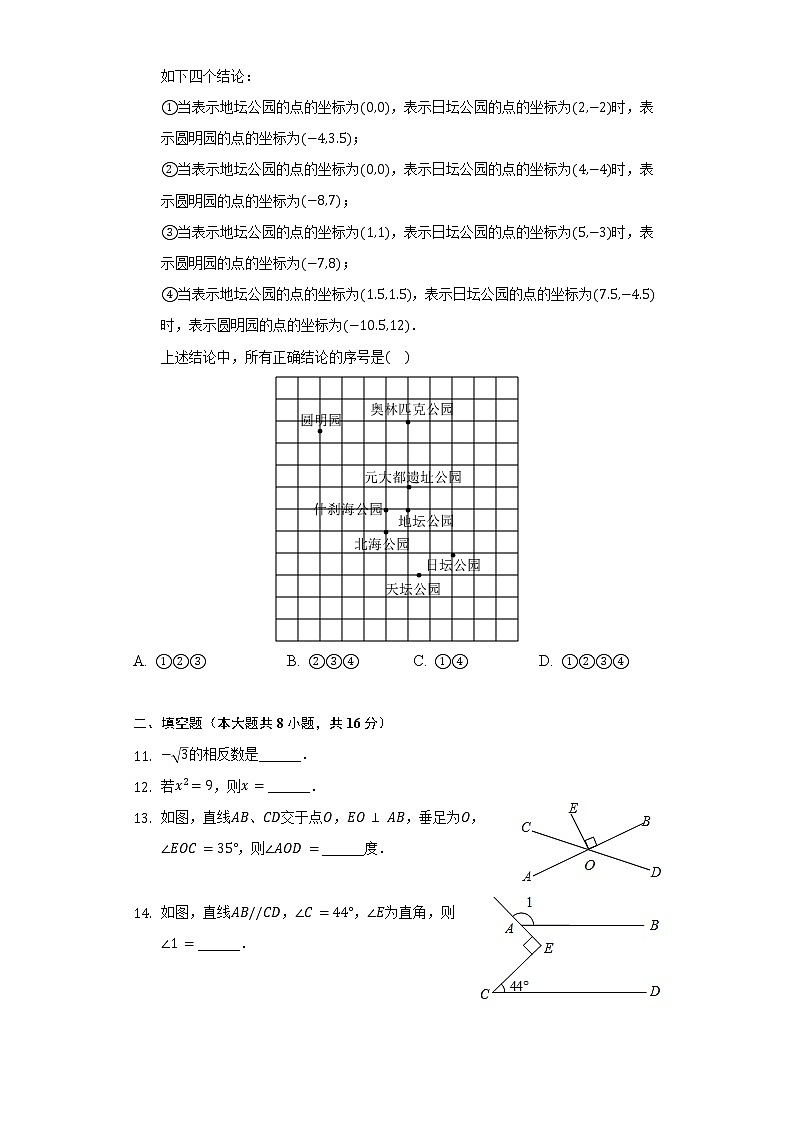
10. 如图是北京市的一些公园分布示意图，小明的全家想在五一节假期去公园赏花踏青．在图中，分别以正东、正北方向为轴、轴的正方向建立平面直角坐标系，有如下四个结论：
    当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为；
    当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为；
    当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为；
    当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为．
    上述结论中，所有正确结论的序号是

A.  B.  C.  D.

二、填空题（本大题共8小题，共16分）

11. 的相反数是______．
12. 若，则______．
13. 如图，直线、交于点，，垂足为，，则______度．
     

14. 如图，直线，，为直角，则______．
    
     

15. 将点向右平移个单位长度到点，且点恰好在轴上，则点坐标是______．
16. 如图，在数轴上方作一个的方格每一方格的边长为个单位，依次连结四边中点，，，得到一个正方形，点落在数轴上，用圆规在点的左侧的数轴上取点，使，若点在原点右侧且到原点的距离为个单位，则点表示的数是______．

17. 如图，为响应国家新能源建设，乐清市公交站亭装上了太阳能电池板当地某一季节的太阳光平行光线与水平线最大夹角为，如图，电池板与最大夹角时刻的太阳光线相垂直，此时电池板与水平线夹角为，要使，需将电池板逆时针旋转度，则为______

18. 定义：在平面直角坐标系中，把从点出发沿纵或横方向到达点至多拐一次弯的路径长称为，的“实际距离”如图若，，则，的“实际距离”为或，，坐标分别为，，，若点满足到，，的“实际距离”相等，则点的坐标为______．

三、解答题（本大题共11小题，共64分）

19. 计算：
    ；
     
20. 解二元一次方程组：
    ；
    ．
21. 填空并完成以下证明：
    已知，如图，，，于，求证：．
    证明：已知
    ______．
    已知
    ______
    ____________
    已知
    ____________
    ______
    ____________
    ．
22. 如图，平面内有两条直线，，点在直线上，按要求画图并填空：
    过点画直线的垂线，垂足为点，点到直线的距离为线段______的长度；
    过点画直线，交直线于点；
    过点画直线．
23. 有些关于方程组的问题，需要求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：
    已知实数，满足，，求和的值．
    本题常规思路是将两式联立组成方程组，解得，的值再代入欲求值的代数式得到答案，常规思路运算量比较大．小明在做题过程仔细观察两个方程未知数的系数之间的关系，发现本题还可以通过适当变形整体求得代数式的值，如由可得，由可得这样的解题思想就是通常所说的“整体思想”．
    请同学们运用这样的思想解决下列问题：
    已知二元一次方程组，则______，______；
    对于实数，，定义新运算：，其中，，是常数，等式右边是通常的加法和乘法运算．已知，，那么求的值．
24. 已知：如图，，交于点，求证：．

25. 已知：，，
    在坐标系中描出各点，画出．
    求的面积；
    设点在坐标轴上，且与的面积相等，求点的坐标．

26. 如图，，．
    判断与的位置关系，并证明；
    若平分，于点，，求的度数．
     

27. 当，都是实数，且满足，就称点为完美点．
    判断点是否为完美点．
    已知关于，的方程组，当为何值时，以方程组的解为坐标的点是完美点，请说明理由．
28. 在平面直角坐标系中，对于，两点给出如下定义：若点到、轴的距离中的最大值等于点到、轴的距离中的最大值，则称，两点为“等距点”下图中的，两点即为“等距点”．
    已知点的坐标为，
    在点，，中，为点的“等距点”的是______；
    若点的坐标为，且，两点为“等距点”，则点的坐标为______；
    若，两点为“等距点”，求的值．

29. 如图，以直角三角形的直角顶点为原点，以，所在直线为轴和轴建立平面直角坐标系，点，满足．
    直接写出点的坐标为______；点的坐标为______．
    如图，已知坐标轴上有两动点，同时出发，点从点出发沿轴负方向以个单位长度每秒的速度匀速移动，点从点出发以个单位长度每秒的速度沿轴正方向移动，点到达点整个运动随之结束．的中点的坐标是，设运动时间为秒，是否存在这样的，使，的面积相等？若存在，请求出的值；若不存在，请说明理由．
    如图，点是线段上一点，满足，点是线段上一动点，连交于点，当点在线段上运动的过程中，的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．

答案和解析

1.【答案】

【解析】解：观察各选项图形可知，选项的图案可以通过平移得到．
故选：．
根据平移只改变图形的位置，不改变图形的形状与大小解答．
本题考查了利用平移设计图案，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．
 

2.【答案】

【解析】解：，，
所给数据中无理数有：，，，不循环共个．
故选：．
根据无理数的三种形式：开方开不尽的数，无限不循环小数，含有的数，找出无理数的个数．
本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：开方开不尽的数，无限不循环小数，含有的数．
 

3.【答案】

【解析】解：、和为的两个角不一定是邻补角，故错误，为假命题；
B、一条直线有无数条垂线，故错误，为假命题；
C、点到直线的距离是指这点到直线的垂线段的长度，故错误，为假命题；
D、两条直线被第三条直线所截，如内错角相等，则同位角必相等，正确，为真命题，
故选D．
利用邻补角的定义、垂线的性质、点到直线的距离及平行线的性质分别判断后即可确定正确的选项．
本题考查了命题与定理的知识，解题的关键是了解邻补角的定义、垂线的性质、点到直线的距离及平行线的性质，难度不大．
 

4.【答案】

【解析】解：、东经，北纬，位置很明确，能确定位置，故本选项正确；
B、北京市四环路，具体位置不能确定，故本选项错误；
C、北偏东，具体位置不能确定，故本选项错误；
D、红星电影院排，具体位置不能确定，故本选项错误．
故选：．
根据位置的确定需要两个条件对各选项分析判断即可得解．
本题考查了坐标确定位置，理解位置的确定需要两个条件是解题的关键．
 

5.【答案】

【解析】

【分析】

本题考查了平方根、立方根及绝对值的化简．题目难度不大，掌握平方根、立方根及绝对值的意义是解决本题的关键．
根据平方根、立方根、绝对值的意义逐个选项判断即可得出结论．
【解答】
解：因为 ，所以 A 正确；
，所以 不正确；
，所以 不正确；
， ，所以 不正确．
故选 A ．
 

6.【答案】

【解析】解：依据垂线段最短，可得测量运动员跳远成绩选取的应是图中线段的长度．
故选：．
利用从直线外一点到这条直线所作的线段中，垂线段最短求解即可．
本题考查了垂线段的性质：垂线段最短．垂线段最短指的是从直线外一点到这条直线所作的线段中，垂线段最短．它是相对于这点与直线上其他各点的连线而言．
 

7.【答案】

【解析】解：的算术平方根是，不是无理数，
再取的平方根，而的平方根为，是无理数，
输出值，
故选：．
根据已知判断每一步输出结果即可得到答案．
本题考查实数分类及计算，判断每步计算结果是否为无理数是解题的关键．
 

8.【答案】

【解析】解：，，
，
故正确；
，
，
，
平分；
故正确；
，
，
，
平分，
；
故正确；
，
，
，
；
故正确．
故正确结论的个数有个．
故选：．
根据平行线的性质可得；由，即可求得的度数，得到平分；由，根据两直线平行，内错角相等，即可求得的度数，的度数；又由，即可求得与的度数．
此题考查了平行线的性质、垂线的定义以及角平分线的定义．此题难度适中，注意掌握数形结合思想的应用．
 

9.【答案】

【解析】解：如图，设，
纸条沿折叠，
，，
，
纸条沿折叠，
，
而，
，
解得，
，
，
．
故选：．
设，根据折叠的性质得，，则，再由第次折叠得到，于是利用平角定义可计算出，接着根据平行线的性质得，所以．
本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．解决本题的关键是画出折叠前后得图形．
 

10.【答案】

【解析】解：当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为，正确；
当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为，正确；
当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为，正确；
当表示地坛公园的点的坐标为，表示日坛公园的点的坐标为时，表示圆明园的点的坐标为，正确．
故选：．
根据各结论所给两个点的坐标得出原点位置及单位长度，从而得出答案．
本题主要考查坐标确定位置，解题的关键是确定原点位置及各点的横纵坐标．
 

11.【答案】

【解析】

【分析】
本题考查了相反数，掌握相反数的定义是解题的关键．
根据相反数的定义进行填空即可．
【解答】
解： 的相反数是 ，
故答案为 ．   

12.【答案】

【解析】解：
．
故答案为．
由于左边为一个平方式，所以可用直接开平方法进行求解．
本题主要考查了求平方根的能力，注意一个正数有两个平方根．
 

13.【答案】

【解析】解：，
．
又，
．
对顶角相等，
，
故答案为：．
根据图形求得；然后由对顶角相等的性质来求的度数．
本题考查了垂线，对顶角、邻补角等知识点．求的度数时，也可以利用邻补角的定义先求得，再由邻补角的定义求的度数．
 

14.【答案】

【解析】

【分析】
本题考查了平行线的性质的应用，能正确作出辅助线是解此题的关键．过 作 ，得出 ，根据平行线的性质得出 ， ，求出 ，即可求出答案．
【解答】
解：过 作 ，

，
，
， ，
， 为直角，
， ，
，
故答案为： ．   

15.【答案】

【解析】解：由题意：，
，
，
．
故答案为．
利用平移的性质构建方程即可解决问题．
本题考查坐标与图形的平移等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

16.【答案】

【解析】解：根据题意，，
，
，
点在原点右侧且到原点的距离为个单位，
原点在、之间，的下方，
到原点的距离为，
表示的数是．
故答案为：．
求得点到原点的距离即可．
本题考查的是有理数在数轴上的表示方法，解题关键是计算出点到原点的距离．
 

17.【答案】

【解析】解：
，
，
，
，
，
，
要使，需将电池板逆时针旋转度，
，
故答案为：．
求出的度数，根据平行线的性质得出，再求出答案即可．
本题考查了平行线的性质，旋转的性质，三角形内角和定理，垂直的定义等知识点，能求出的度数是解此题的关键．
 

18.【答案】

【解析】解：如图，设，根据题目中的“实际距离”的定义可知，点只能在区域内，

，，
到，，的“实际距离”相等，
可得方程组，，
若要使到，，的“实际距离”相等，
由图可知只能在点左侧、点上方的位置，
，
解得，，，
则，
故答案为：．
若设，根据到，，的“实际距离”相等，构建方程组即可求解．
此题主要考查了坐标确定位置等知识，正确理解实际距离的定义并列出方程组是解题关键．
 

19.【答案】解：

；


．

【解析】先化简各式，然后再进行计算即可解答．
本题考查了实数的运算，准确熟练地化简各式是解题的关键．
 

20.【答案】解：，
代入，可得：，
解得，
把代入，解得，
原方程组的解是．

，
由，可得：，
由，可得：，
，可得，
解得，
把代入，可得：，
解得，
原方程组的解是．

【解析】应用代入消元法，求出方程组的解是多少即可．
应用加减消元法，求出方程组的解是多少即可．
此题主要考查了解二元一次方程组的方法，注意代入消元法和加减消元法的应用．
 

21.【答案】  同位角相等，两直线平行    两直线平行，内错角相等    等量代换  同位角相等，两直线平行    两直线平行，同位角角相等

【解析】证明：已知，
．
已知，
同位角相等，两直线平行，
两直线平行，内错角相等．
已知，
等量代换，
同位角相等，两直线平行，
，两直线平行，同位角角相等
．
故答案为：；同位角相等，两直线平行；；两直线平行，内错角相等；；等量代换；同位角相等，两直线平行；；两直线平行，同位角角相等．
先根据垂直的定义得出，再由得出，故可得出，根据得出，所以，由平行线的性质即可得出结论．
本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．
 

22.【答案】

【解析】解：如图，直线即为所求，线段的长是点到直线的距离．
故答案为：；

如图，直线即为所求；
如图，直线即为所求．
根据垂线的定义画出图形即可；
根据垂线的定义画出图形；
根据平行线的定义画出图形即可．
本题考查作图复杂作图，点到直线的距离，平行线的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
 

23.【答案】 

【解析】解：，
得：，
．
得：．
故答案为：，．
由题意得：
得：．
．
整体代换求值．
先将新定义转化为常规运算，再解方程．
本题考查整体代换解方程，确定将哪部分当作一个整体是求解本题的关键．
 

24.【答案】证明：，
两直线平行，内错角相等．
，
．
内错角相等，两直线平行．

【解析】先由，可得，由已知条件，等量代换可得，即可得出答案．
本题主要考查了平行线的判定与性质，熟练应用平行线的判定与性质进行求解是解决本题的关键．
 

25.【答案】解：如图所示：

过点向、轴作垂线，垂足为、．
四边形的面积，的面积，的面积，的面积．
的面积四边形的面积的面积的面积的面积．
当点在轴上时，的面积，即：，解得：，
所点的坐标为或；
当点在轴上时，的面积，即，解得：．
所以点的坐标为或．
所以点的坐标为或或或．

【解析】确定出点、、的位置，连接、、即可；
过点向、轴作垂线，垂足为、，的面积四边形的面积的面积的面积的面积；
当点在轴上时，由的面积，求得：，故此点的坐标为或；当点在轴上时，的面积，解得：所以点的坐标为或．
本题主要考查的是点的坐标与图形的性质，明确的面积四边形的面积的面积的面积的面积是解题的关键．
 

26.【答案】解：，
证明：，
，
，
，
，
；
由得，
，
，
，
平分，，
，
由可知，
，
．

【解析】由可得，从而得到，再结合，可得；
由可得，则有，可得，再结合平分，，可求得，则可求的度数．
本题主要考查了平行线的判定与性质，角平分线的性质，解答的关键是对平行线的判定与性质的掌握与应用．
 

27.【答案】解：，可得，，可得，
，
不是完美点．

，
，
，可得，
，可得，
，
，
，
当时，点是完美点．

【解析】根据完美点的定义判定即可；
用表示、，构建方程即可解决问题；
本题考查二元方程组，点的坐标等知识，解题的关键是理解题意，学会用转化的思想思考问题，属于中考创新题目．
 

28.【答案】解：、；；
，两点为“等距点”，
若时，则或，
解得舍去或．
若时，则，
解得舍去或．
根据“等距点”的定义知，或符合题意．
即的值是或．

【解析】

【分析】
本题主要考查了新定义、平面直角坐标系中点的坐标、点到坐标轴的距离，读懂“等距点”的定义是解题的关键．
找到 、 轴距离最大为 的点即可；
先分析出点 坐标中到 、 轴距离中至少有一个为 的点，再根据“等距点”概念进行解答即可；
分 时， 时两种情况解答即可．
【解答】
解： 点 到 、 轴的距离中最大值为 ，
与 点是“等距点”的点是 、 ．
当点 坐标中到 、 轴距离中至少有一个为 的点有 、 、 ，
这些点中与 符合“等距点”的是 ．
故答案为 、 ； ；
见答案．   

29.【答案】 
如图中，

由条件可知：点从点运动到点时间为秒，点从点运动到点时间为秒，
时，点在线段上，
即，，，
，，
，
，
．

结论：的值不变，其值为．
理由：如图中，作，过点作的平行线，交轴于，则，

，
又，，
，
，
，
，
，
，
，
，
．

【解析】解：．
，，
解得，，
，；
故答案为，．

见答案．
根据绝对值和算术平方根的非负性，求得，的值即可得出答案；
先得出，，，再根据，列出关于的方程，求得的值即可；
如图中，作，过点作的平行线，交轴于，则，想办法证明，即可解决问题．
本题属于三角形综合题，考查了非负数的性质、三角形的面积、平行线的性质等知识，解题的关键是学会添加常用辅助线，学会用转化的思想思考问题．