

2021-2022学年广东省珠海市第二中学高二下学期期中考试数学试题含答案
展开珠海市第二中学2021-2022学年高二下学期期中考试数学试卷
考试范围:选择性必修第二册+第三册第一章;考试时间:120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每题5分)
1.已知函数的导函数为,且,则( )
A. B. C. D.
2.由数字1,2,3组成的各位上没有重复数字的所有三位数的和为( )
A.66 B.666 C.1332 D.2664
3.某小朋友按如上图规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2022对应的指头是( )
A.小指 B.中指 C.食指 D.无名指
4.将6名优秀教师分配到5个不同的学校进行教学交流,每名优秀教师只分配到1个学校,每个学校至少分配1名优秀教师,则不同的分配方案共有( )
A.2400种 B.1800种 C.1200种 D.1600种
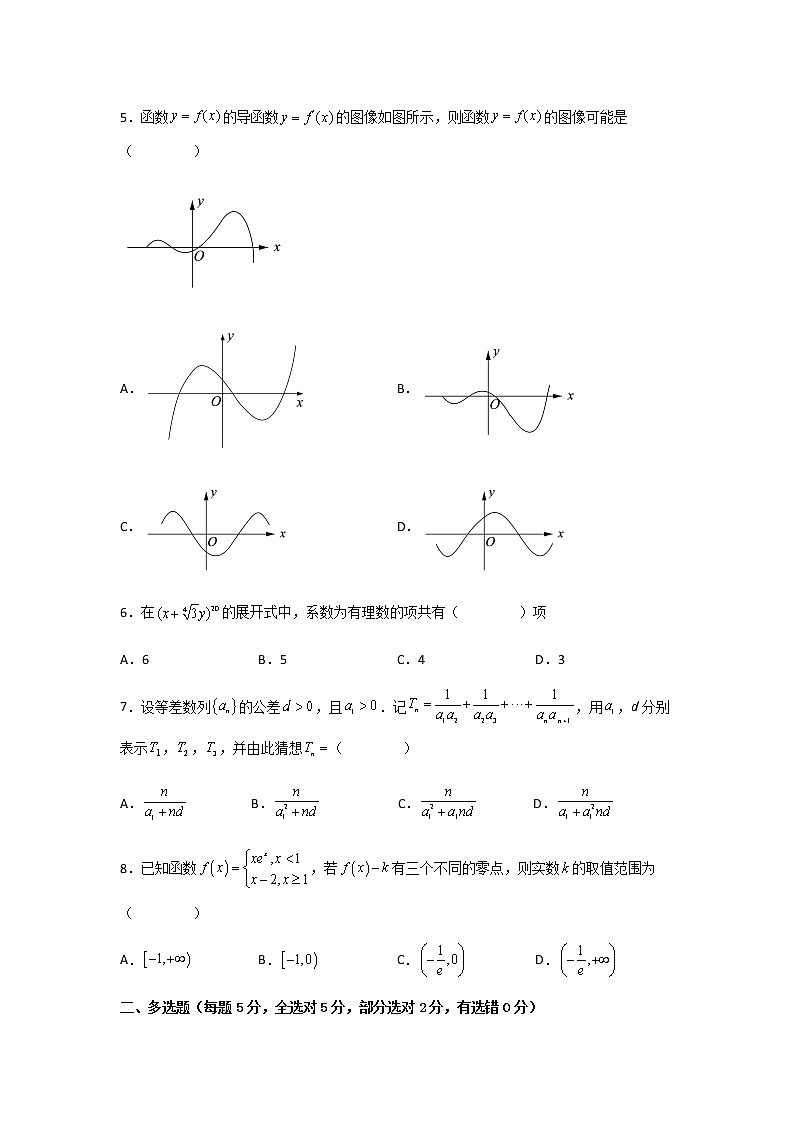
5.函数的导函数的图像如图所示,则函数的图像可能是( )
A. B.
C. D.
6.在的展开式中,系数为有理数的项共有( )项
A.6 B.5 C.4 D.3
7.设等差数列的公差,且.记,用,d分别表示,,,并由此猜想( )
A. B. C. D.
8.已知函数,若有三个不同的零点,则实数的取值范围为( )
A. B. C. D.
二、多选题(每题5分,全选对5分,部分选对2分,有选错0分)
9.数列的前n项和,其第k项满足,则k的值可以为( )
A.9 B.8 C.7 D.6
10.五个人并排站在一起,则下列说法正确的有( )
A.若两人站在一起有48种方法 B.若不相邻共有12种方法
C.若在左边有60种排法 D.若不站在最左边,不站最右边,有72种方法
11.对于函数图像上的任意一点,都存在另外一点,使得的图像在这两个不同点处的切线互相平行,则称函数具有性质,下列函数中不具有性质的有( )
A. B.
C. D.
12.将杨辉三角中的每一个数都换成,得到如图所示的分数三角形,称为莱布尼茨三角形.莱布尼茨三角形具有很多优美的性质,如从第0行开始每一个数均等于其“脚下”两个数之和,如果(),那么下面关于莱布尼茨三角形的结论正确的是( )
第0行
第1行
第2行
第3行
…… ……
第n行 ……
A.当n是偶数时,中间的一项取得最大值;当n是奇数时,中间的两项相等,且同时取得最大值
B.第8行第2个数是
C.(,)
D.(,)
第II卷(非选择题)
三、填空题(每题5分)
13.曲线过点的切线方程是____________.
14.将红、黄、绿三种不同的颜色均涂入图中五个区域中,每个区域涂一种颜色,且相邻的区域不能涂同一种颜色,不同的涂色方法共有__种.(三种颜色必须用全,以数字作答)
15.组合数被9除的余数是______.
16.设函数是定义在上的奇函数,为的导函数,当时,,则使得成立的的取值范围__________.
四、解答题
17.已知函数.
(1)写出函数的单调区间;
(2)求函数在上的最大值、最小值.
18.在(2x-3y)10的展开式中,求:
(1)二项式系数的和;(2)各项系数的和;
(3)奇数项的二项式系数和与偶数项的二项式系数和;
(4)奇数项系数和与偶数项系数和.
19.已知函数,数列满足.数列为等差数列,满足,.
(1)求数列、的通项公式;
(2)求数列的前项和.
20.设数列的前n项和为.已知,
(1)求数列的通项公式;
(2)数列满足,求数列的前n项和.
21.已知函数
(1)讨论的单调性;
(2)设,若方程有三个不同的解,求a的取值范围.
22.已知函数的图像在点处的切线方程为.
(I)用表示出;
(II)若在上恒成立,求的取值范围;
(III)证明:.
参考答案
一、DCDBC ACC 9.AB 10.AC 11.ABD 12.BC
二、13.或
14.42 15.8 16.
三、17.(1)单调递增区间为和,单调递减区间为.
(2)最大值为,最小值为.
18.(1)210 (2)1 (3)29,29 (4)奇数项系数和为,偶数项系数和为
19解:(1)由题意得:,,,等差数列的公差,;
(2)由(1)得:;
20.解:(1)当时,由,得,两式相减得,
所以,,,所以,
所以数列是以1为首项,为公比得等比数列,是以;
(2),
则,
,
两式相减得,
所以.
21.解(1),当时,,函数在单调递增,当时,,得 当时,,函数单调递减,当时,,函数单调递增,综上可知,当时,函数在单调递增,当时,函数的单调递增区间是,函数的单调递减区间是
(2)由,化简为,
设,设,则,,当时,,函数单调递减,当时,,函数单调递增,函数的最大值,
画出函数的图象,由图可知与的交点对应的,一正一负,
如图,画出函数的图象,
当,时,对应的值有3个,
在单调递增,当时,
所以
22. 解(I),,;
又,;
(II)由(I)得:;
令,则在上恒成立;
,
令,解得:,;
(1)当,即时,在上恒成立,
在上单调递增,,满足题意;
(2)当,即时,若,则,则在上单调递减,此时,不合题意;
综上所述:的取值范围为;
(III)由(II)知:当时,在上恒成立,
那么当时,在上恒成立;
令依次取,,,…,可得:
,,,…,,
,
,
,
.
2021-2022学年度高中数学试卷
整体难度:一般
考试范围:函数与导数,计数原理与概率统计,推理与证明,数列
细 / 目 / 表 / 分 / 析
题号 | 难度系数 | 能力维度分析 | 详细知识点 |
一、单选题 | |||
1 | 0.94 | 全部 | 导数(导函数)概念辨析;导数定义中极限的简单计算; |
2 | 0.65 | 全部 | 数字排列问题; |
3 | 0.65 | 全部 | 数与式中的归纳推理; |
4 | 0.85 | 全部 | 排列组合综合;分组分配问题; |
5 | 0.85 | 全部 | 函数与导函数图象之间的关系; |
6 | 0.94 | 全部 | 求有理项或其系数; |
7 | 0.65 | 全部 | 利用定义求等差数列通项公式;裂项相消法求和; |
8 | 0.65 | 全部 | 利用导数求函数的单调区间(不含参);函数单调性、极值与最值的综合应用;利用导数研究函数的零点; |
二、多选题 | |||
1 | 0.65 | 全部 | 利用an与sn关系求通项或项;数列不等式能成立(有解)问题; |
2 | 0.65 | 全部 | 排列组合综合;元素(位置)有限制的排列问题;相邻问题的排列问题;不相邻排列问题; |
3 | 0.85 | 全部 | 导数的运算法则;导数新定义; |
4 | 0.85 | 全部 | 组合数的性质及应用;杨辉三角; |
三、填空题 | |||
1 | 0.85 | 全部 | 求过一点的切线方程; |
2 | 0.85 | 全部 | 涂色问题; |
3 | 0.4 | 全部 | 二项式的系数和;整除和余数问题; |
4 | 0.4 | 全部 | 函数奇偶性的应用;用导数判断或证明已知函数的单调性; |
四、解答题 | |||
1 | 0.85 | 全部 | 利用导数求函数的单调区间(不含参);由导数求函数的最值(不含参); |
2 | 0.65 | 全部 | 求指定项的二项式系数;二项式的系数和;二项展开式各项的系数和;奇次项与偶次项的系数和; |
3 | 0.65 | 全部 | 等差数列通项公式的基本量计算;由定义判定等比数列;分组(并项)法求和; |
4 | 0.65 | 全部 | 错位相减法求和;利用an与sn关系求通项或项; |
5 | 0.65 | 全部 | 利用导数研究函数的零点;利用导数研究函数图象及性质;含参分类讨论求函数的单调区间; |
6 | 0.15 | 全部 | 已知切线(斜率)求参数;利用导数证明不等式;利用导数研究不等式恒成立问题; |
知 / 识 / 点 / 分 / 析
知识模块 | 题量 | 题号 | 难度系数 | 详细知识点 |
函数与导数 |
9
| 1 | 0.94 | 导数(导函数)概念辨析;导数定义中极限的简单计算; |
5 | 0.85 | 函数与导函数图象之间的关系; | ||
8 | 0.65 | 利用导数求函数的单调区间(不含参);函数单调性、极值与最值的综合应用;利用导数研究函数的零点; | ||
11 | 0.85 | 导数的运算法则;导数新定义; | ||
13 | 0.85 | 求过一点的切线方程; | ||
16 | 0.4 | 函数奇偶性的应用;用导数判断或证明已知函数的单调性; | ||
17 | 0.85 | 利用导数求函数的单调区间(不含参);由导数求函数的最值(不含参); | ||
21 | 0.65 | 利用导数研究函数的零点;利用导数研究函数图象及性质;含参分类讨论求函数的单调区间; | ||
22 | 0.15 | 已知切线(斜率)求参数;利用导数证明不等式;利用导数研究不等式恒成立问题; | ||
计数原理与概率统计 |
8
| 2 | 0.65 | 数字排列问题; |
4 | 0.85 | 排列组合综合;分组分配问题; | ||
6 | 0.94 | 求有理项或其系数; | ||
10 | 0.65 | 排列组合综合;元素(位置)有限制的排列问题;相邻问题的排列问题;不相邻排列问题; | ||
12 | 0.85 | 组合数的性质及应用;杨辉三角; | ||
14 | 0.85 | 涂色问题; | ||
15 | 0.4 | 二项式的系数和;整除和余数问题; | ||
18 | 0.65 | 求指定项的二项式系数;二项式的系数和;二项展开式各项的系数和;奇次项与偶次项的系数和; | ||
推理与证明 |
1
| 3 | 0.65 | 数与式中的归纳推理; |
数列 |
4
| 7 | 0.65 | 利用定义求等差数列通项公式;裂项相消法求和; |
9 | 0.65 | 利用an与sn关系求通项或项;数列不等式能成立(有解)问题; | ||
19 | 0.65 | 等差数列通项公式的基本量计算;由定义判定等比数列;分组(并项)法求和; | ||
20 | 0.65 | 错位相减法求和;利用an与sn关系求通项或项; |
2022-2023学年广东省珠海市田家炳中学高二下学期期中数学试题含答案: 这是一份2022-2023学年广东省珠海市田家炳中学高二下学期期中数学试题含答案,共10页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
广东省珠海市第二中学2022-2023学年高二上学期期中考试数学试题及答案: 这是一份广东省珠海市第二中学2022-2023学年高二上学期期中考试数学试题及答案,共12页。
2021-2022学年广东省珠海市高二下学期期末数学试题(A卷)含解析: 这是一份2021-2022学年广东省珠海市高二下学期期末数学试题(A卷)含解析,共14页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












