2020-2021学年四川省内江市八年级（下）期末数学试卷及答案

这是一份2020-2021学年四川省内江市八年级（下）期末数学试卷及答案，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．下列各式中，是分式的是（ ）
A．B．C．D．
2．成人每天维生素D的摄入量约为0.00000046克，将数据0.00000046用科学记数法表示为（ ）
A．4.6×10﹣6B．4.6×10﹣7C．0.46×10﹣6D．46×10﹣6
3．点M位于平面直角坐标系第四象限，且到x轴的距离是5，到y轴的距离是2，则点M的坐标是（ ）
A．（2，﹣5）B．（﹣2，5）C．（5，﹣2）D．（﹣5，2）
4．下列不能判定四边形ABCD是平行四边形的条件是（ ）
A．AB∥CD，AD∥BCB．OA＝OC，OB＝OD
C．AB∥CD，AD＝BCD．AB＝CD，AD＝BC
5．有15名学生参加学校举办的“最强大脑”智力竞赛，比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差，若去掉一个最高分，一个最低分，则一定不会发生变化的是（ ）
A．平均数B．中位数C．众数D．方差
6．下列说法正确的是（ ）
A．对角线相等的四边形是矩形
B．对角线互相垂直且相等的四边形是正方形
C．对角线互相垂直平分的四边形是菱形
D．四边相等的四边形是正方形
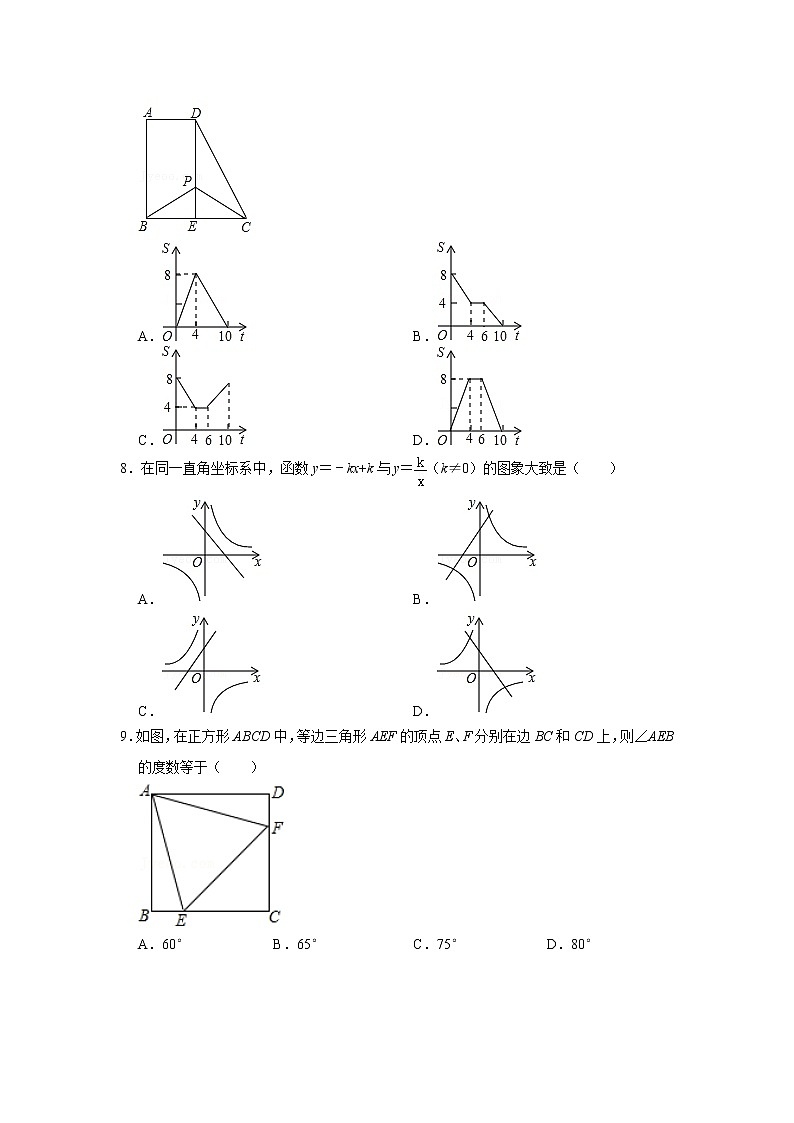
7．如图，在矩形ABED中，AB＝4，BE＝EC＝2，动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动；设点P的运动时间为t秒，△PBC的面积为S，则下列能反映S与t的函数关系的图象是（ ）
A．B．
C．D．
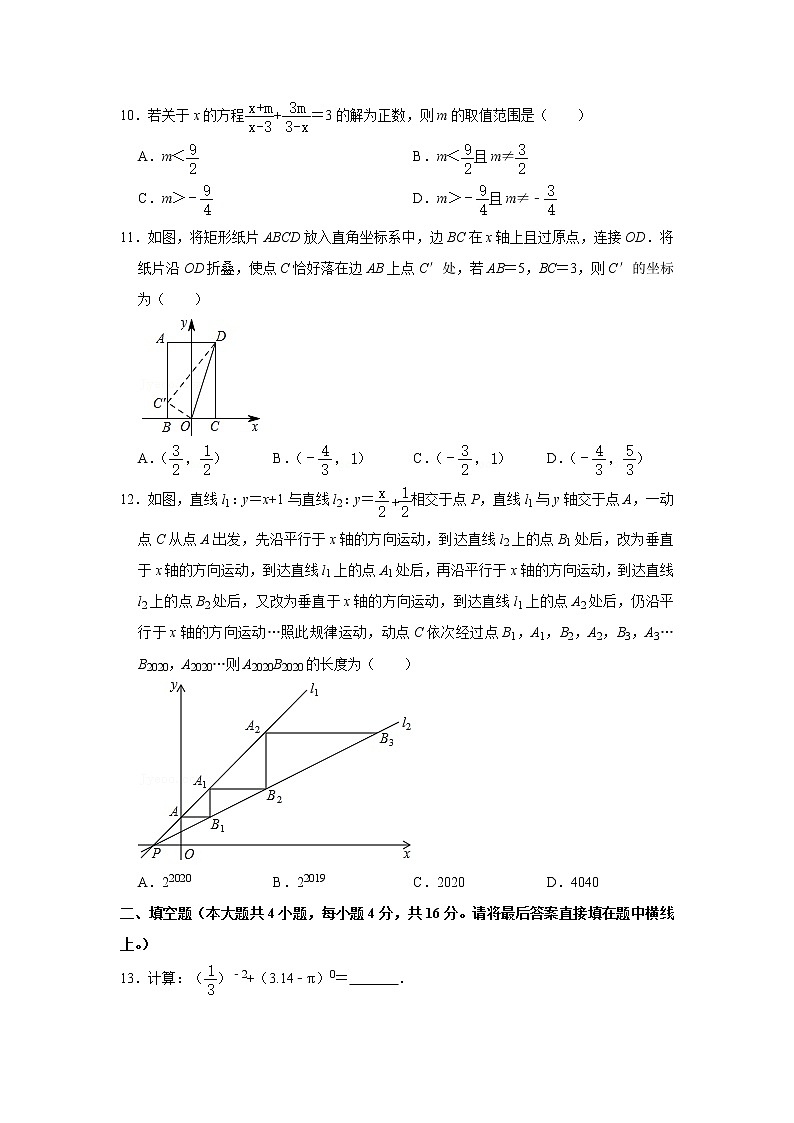
8．在同一直角坐标系中，函数y＝﹣kx+k与y＝（k≠0）的图象大致是（ ）
A．B．
C．D．
9．如图，在正方形ABCD中，等边三角形AEF的顶点E、F分别在边BC和CD上，则∠AEB的度数等于（ ）
A．60°B．65°C．75°D．80°
10．若关于x的方程+＝3的解为正数，则m的取值范围是（ ）
A．m＜B．m＜且m≠
C．m＞﹣D．m＞﹣且m≠﹣
11．如图，将矩形纸片ABCD放入直角坐标系中，边BC在x轴上且过原点，连接OD．将纸片沿OD折叠，使点C恰好落在边AB上点C′处，若AB＝5，BC＝3，则C′的坐标为（ ）
A．（）B．（﹣）C．（﹣）D．（﹣）
12．如图，直线l1：y＝x+1与直线l2：y＝相交于点P，直线l1与y轴交于点A，一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l2上的点B1处后，改为垂直于x轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点B2处后，又改为垂直于x轴的方向运动，到达直线l1上的点A2处后，仍沿平行于x轴的方向运动…照此规律运动，动点C依次经过点B1，A1，B2，A2，B3，A3…B2020，A2020…则A2020B2020的长度为（ ）
A．22020B．22019C．2020D．4040
二、填空题（本大题共4小题，每小题4分，共16分。请将最后答案直接填在题中横线上。）
13．计算：（）﹣2+（3.14﹣π）0＝ ．
14．若＝﹣2，则＝ ．
15．如图，点A，B是反比例函数y＝（x＞0）图象上的两点，过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D，连接OA，BC，已知点C（2，0），BD＝2，S△BCD＝3，则S△AOC＝ ．
16．如图所示，四边形ABCD中，AC⊥BD于点O，AO＝CO＝4，BO＝DO＝3，点P为线段AC上的一个动点．过点P分别作PM⊥AD于点M，作PN⊥DC于点N．连接PB，在点P运动过程中，PM+PN+PB的最小值等于 ．
三、解答题（本大题共6个小题，共56分。解答应写出必要的文字说明或演算步骤。）
17．（10分）（1）化简：÷﹣．
（2）先化简（）÷，再从﹣1，0，1中选择合适的x值代入求值．
18．（7分）如图，在▱ABCD中，点E，F分别是AD，BC上的点，且DE＝BF，分别过点E，F作EG⊥BD，FH⊥BD，垂足分别为G，H，连接EH，FG．请判断四边形HFGE的形状并说明理由．
19．（9分）某中学举办“信息技术知识答题竞赛”，八、九年级根据初赛成绩各选出5名选手组成代表队参加学校决赛，现将两个队各选出的5名选手的决赛成绩绘制成如下统计图表．
（1）根据图表信息填空：a＝ ，b＝ ，c＝ ；
（2）计算九年级代表队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．
20．（9分）为迎接“五一”国际劳动节，某商场计划购进甲、乙两种品牌的T恤衫共100件，已知乙品牌每件的进价比甲品牌每件的进价贵30元，且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍．
（1）求甲、乙两种品牌每件的进价分别是多少元？
（2）商场决定甲品牌以每件50元出售，乙品牌以每件100元出售．为满足市场需求，购进甲种品牌的数量不少于乙种品牌数量的4倍，请你确定获利最大的进货方案，并求出最大利润．
21．（9分）一次函数y＝kx+b与反比例函数y＝的图象相交于A（﹣1，4），B（2，n）两点，直线AB交x轴于点D．
（1）求一次函数与反比例函数的表达式；
（2）观察图象，直接写出不等式kx+b﹣＞0的解集；
（3）过点B作BC⊥y轴，垂足为C，连接AC交x轴于点E，求△AED的面积S．
22．（12分）在平行四边形ABCD中，∠BAD的平分线交线段BC于点E，交线段DC的延长线于点F，以EC，CF为邻边作平行四边形ECFG．
（1）如图1，求证：平行四边形ECFG为菱形；
（2）如图2，若∠ABC＝90°，M是EF的中点，求∠BDM的度数．
2020-2021学年四川省内江市八年级（下）期末数学试卷
参考答案与试题解析
一、选择题
1-5：CBACB 6-10：CDACB 11-12：BB
二、填空题
13．10
14．3
15．5
16．7.8
三、解答题
17．（1）原式＝•﹣
＝﹣
＝；
（2）原式＝÷
＝•
＝，
当x＝﹣1，1时，原式没有意义；
当x＝0时，原式＝﹣1．
18．四边形HFGE是平行四边形，理由如下：
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠ADB＝∠CBD，
∵EG⊥BD，FH⊥BD，
∴∠DGE＝∠EGH＝∠BHF＝∠FHG＝90°，
∴EG∥FH，
∵DE＝BF，
∴△DGE≌△BHF（AAS），
∴GE＝HF，
∴四边形HFGE是平行四边形．
19．（1）由题意，a＝85，b＝＝85，c＝100．
故答案为：85，85，100．
（2）．
∵160＜70，
∴八年级代表队选手成绩较为稳定．
20．（1）设甲品牌每件的进价为x元，则乙品牌每件的进价为（x+30）元，
，
解得，x＝30
经检验，x＝30是原分式方程的解，
∴x+30＝60，
答：甲品牌每件的进价为30元，则乙品牌每件的进价为60元；
（2）设该商场购进甲品牌T恤衫a件，则购进乙品牌T恤衫（100﹣a）件，利润为w元，
∵购进甲种品牌的数量不少于乙种品牌数量的4倍，
∴a≥4（100﹣a）
解得，a≥80
w＝（50﹣30）a+（100﹣60）（100﹣a）＝﹣20a+4000，
∵a≥80，
∴当a＝80时，w取得最大值，此时w＝2400元，100﹣a＝20，
答：获利最大的进货方案是：购进甲品牌T恤衫80件，购进乙品牌T恤衫20件，最大利润是2400元．
21．（1）把A（﹣1，4）代入反比例函数y＝得，m＝﹣1×4＝﹣4，
所以反比例函数的解析式为y＝﹣；
把B（2，n）代入y＝﹣得，2n＝﹣4，
解得n＝﹣2，
所以B点坐标为（2，﹣2），
把A（﹣1，4）和B（2，﹣2）代入一次函数y＝kx+b得，
，
解得，
所以一次函数的解析式为y＝﹣2x+2；
（2）观察图象，不等式kx+b﹣＞0的解集为x＜﹣1或0＜x＜2；
（3）∵BC⊥y轴，垂足为C，B（2，﹣2），
∴C点坐标为（0，﹣2）．
设直线AC的解析式为y＝px+q，
∵A（﹣1，4），C（0，﹣2），
∴，
解，
∴直线AC的解析式为y＝﹣6x﹣2，
当y＝0时，﹣6x﹣2＝0，解得x＝﹣，
∴E点坐标为（﹣，0），
∵直线AB的解析式为y＝﹣2x+2，
∴直线AB与x轴交点D的坐标为（1，0），
∴DE＝1﹣（﹣）＝，
∴△AED的面积S＝＝．
22．（1）证明：∵AF平分∠BAD，
∴∠BAF＝∠DAF，
∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
∴∠DAF＝∠CEF，∠BAF＝∠CFE，
∴∠CEF＝∠CFE，
∴CE＝CF，
又∵四边形ECFG是平行四边形，
∴四边形ECFG为菱形．
（2）解：如图2，连接BM，MC，
∵∠ABC＝90°，四边形ABCD是平行四边形，
∴四边形ABCD是矩形，
∴∠BCD＝90°，
∴∠ECF＝90°，
由（1）可知，四边形ECFG为菱形，
∴四边形ECFG为正方形．
∵∠BAF＝∠DAF，
∴BE＝AB＝DC，
∵M为EF中点，
∴∠CEM＝∠ECM＝45°，
∴∠BEM＝∠DCM＝135°，
在△BME和△DMC中，
，
∴△BME≌△DMC（SAS），
∴MB＝MD，
∠DMC＝∠BME．
∴∠BMD＝∠BME+∠EMD＝∠DMC+∠EMD＝90°，
∴△BMD是等腰直角三角形，
∴∠BDM＝45°．平均分
（分）
中位数
（分）
众数
（分）
方差
（分2）
八年级
85
a
85
70
九年级
b
80
c
s2