2020-2021学年浙江省杭州市上城区八年级（下）期末数学试卷

这是一份2020-2021学年浙江省杭州市上城区八年级（下）期末数学试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年浙江省杭州市上城区八年级（下）期末数学试卷
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1．（3分）下列各式中，为最简二次根式的是（　　）
A． B． C． D．
2．（3分）随机抽取八年级（1）班5名同学的跳绳测试成绩（单位：个）如下：168，170，170，172，185．这组数据的众数是（　　）
A．168 B．170 C．171 D．173
3．（3分）如图，在平行四边形ABCD中，∠A＝150°，则∠B的度数是（　　）

A．30° B．75° C．100° D．150°
4．（3分）如图，矩形纸片ABCD中，AB＝6cm，BC═8cm，现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为（　　）

A．2cm B．3cm C．4cm D．6cm
5．（3分）一元二次方程x2﹣6x﹣5＝0配方后可变形为（　　）
A．（x﹣3）2＝14 B．（x﹣3）2＝4 C．（x+3）2＝14 D．（x+3）2＝4
6．（3分）用反证法证明命题：“已知△ABC，AB＝AC，求证：∠B＜90°．”第一步应先假设（　　）
A．∠B≥90° B．∠B＞90° C．∠B＜90° D．AB≠AC
7．（3分）下列方程的根是无理数的是（　　）
A．（x+）（x﹣）＝﹣4 B．（2x﹣1）2＝（3x+1）2
C．x2+4x﹣3＝0 D．2x2﹣7x＝0
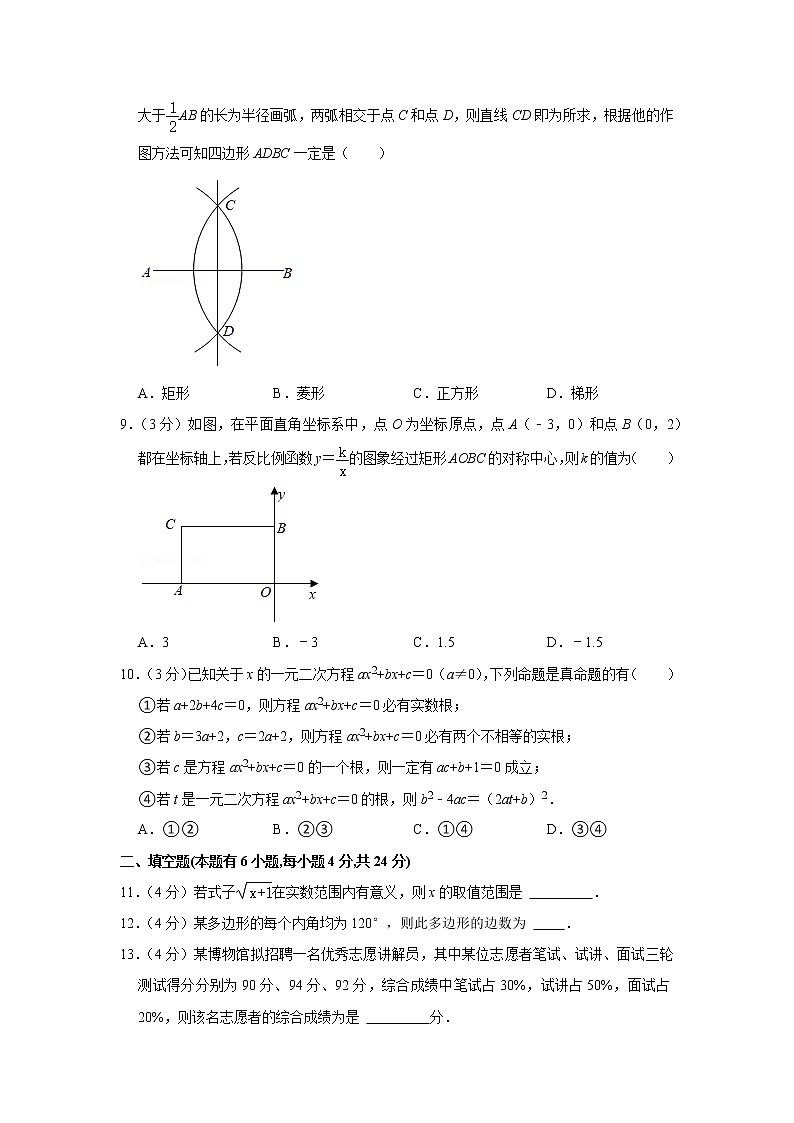
8．（3分）方方同学在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于点C和点D，则直线CD即为所求，根据他的作图方法可知四边形ADBC一定是（　　）

A．矩形 B．菱形 C．正方形 D．梯形
9．（3分）如图，在平面直角坐标系中，点O为坐标原点，点A（﹣3，0）和点B（0，2）都在坐标轴上，若反比例函数y＝的图象经过矩形AOBC的对称中心，则k的值为（　　）

A．3 B．﹣3 C．1.5 D．﹣1.5
10．（3分）已知关于x的一元二次方程ax2+bx+c＝0（a≠0），下列命题是真命题的有（　　）
①若a+2b+4c＝0，则方程ax2+bx+c＝0必有实数根；
②若b＝3a+2，c＝2a+2，则方程ax2+bx+c＝0必有两个不相等的实根；
③若c是方程ax2+bx+c＝0的一个根，则一定有ac+b+1＝0成立；
④若t是一元二次方程ax2+bx+c＝0的根，则b2﹣4ac＝（2at+b）2．
A．①② B．②③ C．①④ D．③④
二、填空题(本题有6小题,每小题4分,共24分)
11．（4分）若式子在实数范围内有意义，则x的取值范围是 　 　．
12．（4分）某多边形的每个内角均为120°，则此多边形的边数为 　 　．
13．（4分）某博物馆拟招聘一名优秀志愿讲解员，其中某位志愿者笔试、试讲、面试三轮测试得分分别为90分、94分、92分，综合成绩中笔试占30%，试讲占50%，面试占20%，则该名志愿者的综合成绩为是 　 　分．
14．（4分）关于x的一元二次方程mx2+3x+m2﹣2m＝0有一个解是0，则m＝　 　．
15．（4分）正比例函数y1＝k1x（k1≠0）与反比例函数y2＝（k2≠0）的图象的一个交点是M（﹣3，2），若y2＜y1，则x的取值范围是 　 　．
16．（4分）在等腰Rt△ABC中，底边BC＝2，作矩形BCDE，使其面积为6，分别取AB和BE的中点F和G，连结FG，则线段FG的长为 　 　．
三、解答题(本题有7小题,第17题6分,第18、19题每题8分,第20、21题每题10分,第22、23题每题12分,共66分)
17．（6分）计算和解方程：
（1）计算：﹣+；
（2）解方程：a（a﹣3）﹣a+3＝0．
18．（8分）某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲、乙两名队员在五天中进球数（单位：个）进行统计，结果如表；
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算，甲进球的平均数为8，方差为3.2．
（1）求乙进球的平均数和方差；
（2）如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？
19．（8分）如图，在▱ABCD中，点E、F为对角线BD的三等分点，连接AE，CF，AF，CE．
（1）求证：四边形AECF为平行四边形；
（2）若四边形AECF为菱形，且AE＝BE，求∠BAD的度数．

20．（10分）圆圆想买一个蓝牙耳机，家边上数码城售卖的某款蓝牙耳机，原来每只售价400元，经过连续两次降价后，现在每只售价256元．
（1）求平均每次降价的百分率；
（2）某电商平台“618”搞活动，同款蓝牙耳机原价是300元，现在7折优惠，包邮到家．同时，数码城按照前两次的平均降价率进行第三次降价．请问：圆圆选择哪种方式购买比较合算？请通过计算说明．
21．（10分）如图，在矩形ABCD中，AD＝5，AB＝3，E是BC上一点（不包括B，C两端点），连结AE和DE，作DF⊥AE于点F．
（1）若AE＝AD，求证：△ADF≌△EAB；
（2）在（1）条件下，求△DEF的面积；
（3）设AE＝x，DF＝y，请求y关于x的函数关系式及自变量x的取值范围．

22．（12分）为了节能减排，某公司从2018年开始投入技术改进资金，经技术改进后产品的成本不断降低，具体数据如表：
年度
2018
2019
2020
2021
投入技术改进资金x万元
2.5
3
4
4.5
产品成本y万元
14.4
12
9
8
（1）分析表中数据，请从一次函数和反比例函数中确定一个函数表示其变化规律，求出y与x的函数关系式，并说明理由；
（2）若2022年公司打算投入技术改进资金5万元，预计2022年产品成本比2021年降低多少万元？
（3）若2023年公司打算把投入技术改进资金x和产品成本y之和控制在12万元，请分别求出投入技术改进资金和产品成本．
23．（12分）在正方形ABCD中，点E、F分别是边AD和DC上一点，且DE＝DF，连结CE和AF，点G是射线CB上一点，连结EG，满足EG＝EC，AF交EG于点M，交EC于点N．
（1）证明：∠DAF＝∠DCE；
（2）求线段EG与线段AF的关系（位置与数量关系），并说明理由；
（3）是否存在实数m，当AM＝mAF时，BC＝3BG？若存在，请求出m的值；若不存在，请说明理由．


2020-2021学年浙江省杭州市上城区八年级（下）期末数学试卷
参考答案与试题解析
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1．（3分）下列各式中，为最简二次根式的是（　　）
A． B． C． D．
【分析】根据最简二次根式的概念判断即可．
【解答】解：A、＝＝2，被开方数中含能开得尽方的因数，不是最简二次根式，不符合题意；
B、＝，被开方数含分母，不是最简二次根式，不符合题意；
C、＝a，被开方数中含能开得尽方的因式，不是最简二次根式，不符合题意；
D、是最简二次根式，符合题意；
故选：D．
【点评】本题考查的是最简二次根式的概念，掌握被开方数不含分母、被开方数中不含能开得尽方的因数或因式的二次根式，叫做最简二次根式是解题的关键．
2．（3分）随机抽取八年级（1）班5名同学的跳绳测试成绩（单位：个）如下：168，170，170，172，185．这组数据的众数是（　　）
A．168 B．170 C．171 D．173
【分析】根据众数的定义，找出这组数据中出现次数最多的数，即可求出答案．
【解答】解：在这组数据：168，170，170，172，185中，
170出现了2次，出现的次数最多，
则这组数据的众数是170．
故选：B．
【点评】此题考查了众数，掌握众数的定义是本题的关键，众数是一组数据中出现次数最多的数．
3．（3分）如图，在平行四边形ABCD中，∠A＝150°，则∠B的度数是（　　）

A．30° B．75° C．100° D．150°
【分析】由平行四边形的性质可得AD∥BC，由平行线的性质可求解．
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠A+∠B＝180°，
∴∠B＝180°﹣∠A＝30°，
故选：A．
【点评】本题考查了平行四边形的性质，掌握平行四边形的性质是本题的关键．
4．（3分）如图，矩形纸片ABCD中，AB＝6cm，BC═8cm，现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为（　　）

A．2cm B．3cm C．4cm D．6cm
【分析】根据翻折的性质可得∠B＝∠AB1E＝90°，AB＝AB1，然后求出四边形ABEB1是正方形，再根据正方形的性质可得BE＝AB，然后根据CE＝BC﹣BE，代入数据进行计算即可得解．
【解答】解：∵沿AE对折点B落在边AD上的点B1处，
∴∠B＝∠AB1E＝90°，AB＝AB1，
又∵∠BAD＝90°，
∴四边形ABEB1是正方形，
∴BE＝AB＝6cm，
∴CE＝BC﹣BE＝8﹣6＝2cm．
故选：A．
【点评】本题考查了矩形的性质，正方形的判定与性质，翻折变换的性质，判断出四边形ABEB1是正方形是解题的关键．
5．（3分）一元二次方程x2﹣6x﹣5＝0配方后可变形为（　　）
A．（x﹣3）2＝14 B．（x﹣3）2＝4 C．（x+3）2＝14 D．（x+3）2＝4
【分析】先把方程的常数项移到右边，然后方程两边都加上32，这样方程左边就为完全平方式．
【解答】解：x2﹣6x﹣5＝0，
x2﹣6x＝5，
x2﹣6x+9＝5+9，
（x﹣3）2＝14，
故选：A．
【点评】本题考查了利用配方法解一元二次方程ax2+bx+c＝0（a≠0）：先把二次系数变为1，即方程两边除以a，然后把常数项移到方程右边，再把方程两边加上一次项系数的一半．
6．（3分）用反证法证明命题：“已知△ABC，AB＝AC，求证：∠B＜90°．”第一步应先假设（　　）
A．∠B≥90° B．∠B＞90° C．∠B＜90° D．AB≠AC
【分析】直接利用反证法的第一步分析得出答案．
【解答】解：用反证法证明命题：“已知△ABC，AB＝AC，求证：∠B＜90°．”第一步应先假设∠B≥90°．
故选：A．
【点评】此题主要考查了反证法，反证法的一般步骤是：①假设命题的结论不成立；②从这个假设出发，经过推理论证，得出矛盾；③由矛盾判定假设不正确，从而肯定原命题的结论正确．
7．（3分）下列方程的根是无理数的是（　　）
A．（x+）（x﹣）＝﹣4 B．（2x﹣1）2＝（3x+1）2
C．x2+4x﹣3＝0 D．2x2﹣7x＝0
【分析】先求出选项中每个方程的解，再逐个判断即可．
【解答】解：A．（x+）（x﹣）＝﹣4，
x2﹣5＝﹣4，
x2＝1，
x＝±1，即方程的根是有理数，不是无理数，故本选项不符合题意；
B．（2x﹣1）2＝（3x+1）2，
开方得：2x﹣1＝±（3x+1），
解得：x1＝﹣2，x2＝0，即方程的根是有理数，不是无理数，故本选项不符合题意；
C．x2+4x﹣3＝0，
x2+4x＝3，
配方，得x2+4x+4＝3+4，
（x+2）2＝7，
开方，得x+2＝，
解得：x1＝﹣2+，x2＝﹣2﹣，即方程的根是无理数，故本选项符合题意；
D．2x2﹣7x＝0，
x（2x﹣7）＝0，
x＝0或2x﹣7＝0，，
解得：x1＝0，x2＝，即方程的根是有理数，不是无理数，故本选项不符合题意；
故选：C．
【点评】本题考查了解一元二次方程和根的判别式，能选择适当的方法解一元二次方程是解此题的关键，注意：解一元二次方程的方法有：直接开平方法，公式法，配方法，因式分解法等．
8．（3分）方方同学在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于点C和点D，则直线CD即为所求，根据他的作图方法可知四边形ADBC一定是（　　）

A．矩形 B．菱形 C．正方形 D．梯形
【分析】利用作法得到AC＝AD＝BC＝BD，然后根据菱形的判定方法进行判断．
【解答】解：连接AC、AD、BC、BD，如图，
由作法得AC＝AD＝BC＝BD，
所以四边形ADBC为菱形，
所以CD垂直平分AB．
故选：B．

【点评】本题考查了作图﹣复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质和特殊四边形的判定方法．
9．（3分）如图，在平面直角坐标系中，点O为坐标原点，点A（﹣3，0）和点B（0，2）都在坐标轴上，若反比例函数y＝的图象经过矩形AOBC的对称中心，则k的值为（　　）

A．3 B．﹣3 C．1.5 D．﹣1.5
【分析】先求出矩形的中心点，然后根据待定系数法即可求得．
【解答】解：∵点A（﹣3，0）和点B（0，2）都在坐标轴上，
∴矩形AOBC的中心点为（﹣，1），
∵反比例函数y＝的图象经过矩形AOBC的对称中心，
∴k＝﹣×1＝﹣，
故选：D．
【点评】本题考查了待定系数法求反比例函数的解析式，求得矩形的中心点是解题的关键．
10．（3分）已知关于x的一元二次方程ax2+bx+c＝0（a≠0），下列命题是真命题的有（　　）
①若a+2b+4c＝0，则方程ax2+bx+c＝0必有实数根；
②若b＝3a+2，c＝2a+2，则方程ax2+bx+c＝0必有两个不相等的实根；
③若c是方程ax2+bx+c＝0的一个根，则一定有ac+b+1＝0成立；
④若t是一元二次方程ax2+bx+c＝0的根，则b2﹣4ac＝（2at+b）2．
A．①② B．②③ C．①④ D．③④
【分析】①正确，利用判别式判断即可．
②错误，a＝﹣2时，方程有相等的实数根．
③错误，c＝0时，结论不成立．
④正确，利用求根公式，判断即可．
【解答】解：①∵a+2b+4c＝0，
∴a＝﹣2b﹣4c，
∴方程为（﹣2b﹣4c）x2+bx+c＝0，
∴Δ＝b2﹣4（﹣2b﹣4c）•c＝b2+8bc+16c2＝（b+4c）2≥0，
∴方程ax2+bx+c＝0必有实数根，故①正确．
②∵b＝3a+2，c＝2a+2，
∴方程为ax2+（3a+2）x+2a+2＝0，
∴Δ＝（3a+2）2﹣4a（2a+2）＝a2+4a+4＝（a+2）2，
当a＝﹣2时，Δ＝0，方程有相等的实数根，故②错误，
③当c＝0时，c是方程ax2+bx＝0的根，但是b+1不一定等于0，故③错误．
④∵t是一元二次方程ax2+bx+c＝0的根，
∴t＝，
∴2at+b＝±，
∴b2﹣4ac＝（2at+b）2，故④正确，
故选：C．
【点评】本题考查命题与定理，一元二次方程的根的判别式等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
二、填空题(本题有6小题,每小题4分,共24分)
11．（4分）若式子在实数范围内有意义，则x的取值范围是 　x≥﹣1　．
【分析】根据二次根式的定义可知被开方数必须为非负数，列不等式求解．
【解答】解：根据题意得：x+1≥0，
解得x≥﹣1，
故答案为：x≥﹣1．
【点评】主要考查了二次根式的意义和性质．
概念：式子（a≥0）叫二次根式．
性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．
12．（4分）某多边形的每个内角均为120°，则此多边形的边数为 　6　．
【分析】首先可求得每个外角为60°，然后根据外角和为360°即可求得多边形的边数．
【解答】解：180°﹣120°＝60°，
360°÷60°＝6．
即此多边形的边数为6．
故答案为：6．
【点评】本题主要考查的是正多边形的内角和与外角和，掌握正多边形的一个内角与它相邻的一个外角互补，边数×一个外角＝360°是解题的关键．
13．（4分）某博物馆拟招聘一名优秀志愿讲解员，其中某位志愿者笔试、试讲、面试三轮测试得分分别为90分、94分、92分，综合成绩中笔试占30%，试讲占50%，面试占20%，则该名志愿者的综合成绩为是 　92.4　分．
【分析】根据加权平均数的定义列式计算即可．
【解答】解：该名志愿者的综合成绩为90×30%+94×50%+92×20%＝92.4（分），
故答案为：92.4．
【点评】本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．
14．（4分）关于x的一元二次方程mx2+3x+m2﹣2m＝0有一个解是0，则m＝　2　．
【分析】将方程的解0代入，求出m的值，然后将m的值代入求出方程的解．
【解答】解：将x＝0代入得：m2﹣2m＝0，
解得：m1＝0，m2＝2．
∵方程为一元二次方程，
∴m≠0．
故答案为：2．
【点评】本题考查了一元二次方程的解，解答本题的关键是将方程的解代入求出m的值．
15．（4分）正比例函数y1＝k1x（k1≠0）与反比例函数y2＝（k2≠0）的图象的一个交点是M（﹣3，2），若y2＜y1，则x的取值范围是 　x＜﹣3或0＜x＜3　．
【分析】如图，一次函数y1＝k1x（k1≠0）与反比例函数y2＝（k2≠0）的图象相交于点M、N，则N（3，﹣2），然后结合函数图象，写出y2＜y1对应的x的取值范围．
【解答】解：如图，一次函数y1＝k1x（k1≠0）与反比例函数y2＝（k2≠0）的图象相交于点M、N，
∴M、N点关于原点对称，
∴N（3，﹣2），
∴若y2＜y1，则x的取值范围是x＜﹣3或0＜x＜3．
故答案为：x＜﹣3或0＜x＜3．

【点评】本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解；两交点坐标满足两函数解析式．
16．（4分）在等腰Rt△ABC中，底边BC＝2，作矩形BCDE，使其面积为6，分别取AB和BE的中点F和G，连结FG，则线段FG的长为 　或　．
【分析】分两种情况讨论，利用矩形的性质和等腰直角三角形的性质可求EN，AN的长，在Rt△AEN中，由勾股定理可求AE，由三角形的中位线定理可求解．
【解答】解：如图1，连接AE，过点A作AH⊥BC，交BC于H，交DE于N，

∵四边形BCDE是矩形，
∴∠EBC＝∠BED＝90°，
又∵NH⊥BC，
∴四边形EBHN是矩形，
∴EN＝BH，BE＝HN，∠ANE＝90°，
∵S矩形BCDE＝BC×BE＝6，BC＝2，
∴BE＝3，
∵AB＝AC，∠BAC＝90°，AH⊥BC，
∴AH＝BH＝HC＝1，
∴EN＝BH＝1，AN＝HN﹣AN＝2，
∴AE＝＝＝，
∵点F是AB的中点，点G是BE的中点，
∴AE＝2GF，
∴GF＝；
如图2，连接AE，过点A作AH⊥BC，交BC于H，交DE于N，

同理可求GF＝，
综上所述：GF＝或，
故答案为：或．
【点评】本题考查了矩形的判定和性质，勾股定理，三角形中位线定理，利用分类讨论思想解决问题是解题的关键．
三、解答题(本题有7小题,第17题6分,第18、19题每题8分,第20、21题每题10分,第22、23题每题12分,共66分)
17．（6分）计算和解方程：
（1）计算：﹣+；
（2）解方程：a（a﹣3）﹣a+3＝0．
【分析】（1）先根据二次根式的性质进行计算，再合并同类二次根式即可；
（2）先把方程的左边分解因式，再得出两个一元一次方程，最后求出方程的解即可．
【解答】解：（1）原式＝3﹣+3
＝2+3；

（2）a（a﹣3）﹣a+3＝0，
a（a﹣3）﹣（a﹣3）＝0，
（a﹣3）（a﹣1）＝0，
a﹣3＝0或a﹣1＝0，
解得：a1＝3，a2＝1．
【点评】本题考查了二次根式的加减和解一元二次方程，能正确根据二次根式的加减法则进行计算是解（1）的关键，能把一元二次方程转化成一元一次方程是解（2）的关键．
18．（8分）某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲、乙两名队员在五天中进球数（单位：个）进行统计，结果如表；
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算，甲进球的平均数为8，方差为3.2．
（1）求乙进球的平均数和方差；
（2）如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？
【分析】（1）根据平均数、方差的计算公式计算即可；
（2）根据平均数相同时，方差越大，波动越大，成绩越不稳定；方差越小，波动越小，成绩越稳定进行解答．
【解答】解：（1）乙进球的平均数为：（7+9+7+8+9）÷5＝8，
乙进球的方差为：[（7﹣8）2+（9﹣8）2+（7﹣8）2+（8﹣8）2+（9﹣8）2]＝0.8；

（2）∵二人的平均数相同，而S甲2＝3.2，S乙2＝0.8，
∴S甲2＞S乙2，
∴乙的波动较小，成绩更稳定，
∴应选乙去参加定点投篮比赛．
【点评】本题考查方差的定义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．也考查了平均数．
19．（8分）如图，在▱ABCD中，点E、F为对角线BD的三等分点，连接AE，CF，AF，CE．
（1）求证：四边形AECF为平行四边形；
（2）若四边形AECF为菱形，且AE＝BE，求∠BAD的度数．

【分析】（1）由平行四边形的性质可得AB＝CD，AB∥CD，由“SAS”可证△ABE≌△CDF，可得AE＝CF，∠AEB＝∠CFD，由平行四边形的判定可得结论；
（2）由菱形的性质可得AE＝BE＝EF＝AF＝DF，可证△AEF是等边三角形，由等边三角形的性质可求解．
【解答】证明：（1）∵四边形AECF是平行四边形，
∴AB＝CD，AB∥CD，
∴∠ABD＝∠CDB，
∵点E、F为对角线BD的三等分点，
∴BE＝EF＝DF，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（SAS），
∴AE＝CF，∠AEB＝∠CFD，
∴∠AEF＝∠CFE，
∴AE∥CF，
∴四边形AECF是平行四边形；
（2）∵四边形AECF是菱形，
∴AE＝AF＝CF＝CE，
又∵AE＝BE，
∴AE＝BE＝EF＝AF＝DF，
∴∠EAB＝∠EBA，∠EAF＝∠EFA，∠FAD＝∠FDA，△AEF是等边三角形，
∴∠EAF＝∠AFE＝∠AEF＝60°，
∴∠BAE＝30°，∠FAD＝30°，
∴∠BAD＝120°．
【点评】本题考查了平行四边形的性质，菱形的性质，全等三角形的判定和性质，证明△AEF是等边三角形是解题的关键．
20．（10分）圆圆想买一个蓝牙耳机，家边上数码城售卖的某款蓝牙耳机，原来每只售价400元，经过连续两次降价后，现在每只售价256元．
（1）求平均每次降价的百分率；
（2）某电商平台“618”搞活动，同款蓝牙耳机原价是300元，现在7折优惠，包邮到家．同时，数码城按照前两次的平均降价率进行第三次降价．请问：圆圆选择哪种方式购买比较合算？请通过计算说明．
【分析】（1）设平均每次降价的百分率为x，理由经过两次降价后的价格＝原售价×（1﹣降价率）2，即可得出关于x的一元二次方程，解之取其符合题意的值即可得出结论；
（2）利用在电商平台购买所需费用＝原售价×折扣率可求出在电商平台购买所需费用，利用在数码城购买所需费用＝经过两次降价后的价格×（1﹣下降率）可求出在数码城购买所需费用，再比较后即可得出结论．
【解答】解：（1）设平均每次降价的百分率为x，
依题意得：400（1﹣x）2＝256，
解得：x1＝0.2＝20%，x2＝1.8（不合题意，舍去）．
答：平均每次降价的百分率为20%．
（2）选择在数码城购买比较合算，理由如下：
在电商平台购买所需费用为300×0.7＝210（元），
在数码城购买所需费用为256×（1﹣20%）＝204.8（元）．
∵210＞204.8，
∴选择在数码城购买比较合算．
【点评】本题考查了一元二次方程的应用，解题的关键是：（1）找准等量关系，正确列出一元二次方程；（2）根据各数量之间的关系，列式计算．
21．（10分）如图，在矩形ABCD中，AD＝5，AB＝3，E是BC上一点（不包括B，C两端点），连结AE和DE，作DF⊥AE于点F．
（1）若AE＝AD，求证：△ADF≌△EAB；
（2）在（1）条件下，求△DEF的面积；
（3）设AE＝x，DF＝y，请求y关于x的函数关系式及自变量x的取值范围．

【分析】（1）由矩形的性质得∠B＝90°，AD∥BC，则∠DAF＝∠AEB，再由AAS即可证明△ADF≌△EAB；
（2）由全等三角形的性质得DF＝AB＝3，再由勾股定理求出AF＝4，则EF＝AE﹣AF＝1，然后由三角形面积公式求解即可；
（3）由三角形面积公式得S△ADE＝AD•CD＝AE•DF，则AE•DF＝AD•CD，得出y＝，再由AB＜AE＜得3＜x＜即可．
【解答】（1）证明：∵四边形ABCD是矩形，
∴∠B＝90°，AD∥BC，
∴∠DAF＝∠AEB，
∵DF⊥AE，
∴∠AFD＝∠B＝90°，
在△ADF和△EAB中，
，
∴△ADF≌△EAB（AAS）；
（2）解：∵△ADF≌△EAB，
∴DF＝AB＝3，
在Rt△ADF中，由勾股定理得：AF＝＝＝4，
∵AE＝AD＝5，
∴EF＝AE﹣AF＝5﹣4＝1，
∴S△DEF＝DF•EF＝×3×1＝；
（3）解：∵四边形ABCD是矩形，
∴CD＝AB＝3，BC＝AD＝5，∠CDA＝90°，AD∥BC，
∴S△ADE＝AE•DF＝AD•CD，
则AE•DF＝AD•CD，
即xy＝5×3＝15
∴y＝，
∵E是BC上一点（不包括B，C两端点），
∴AB＜AE＜，
∵＝＝，
∴自变量x的取值范围：3＜x＜．
【点评】本题是四边形综合题目，考查了矩形的性质、全等三角形的判定与性质、平行线的性质、勾股定理以及三角形面积等知识；本题综合性强，熟练掌握矩形的性质和勾股定理，证明△ADF≌△EAB是解题的关键，属于中考常考题型．
22．（12分）为了节能减排，某公司从2018年开始投入技术改进资金，经技术改进后产品的成本不断降低，具体数据如表：
年度
2018
2019
2020
2021
投入技术改进资金x万元
2.5
3
4
4.5
产品成本y万元
14.4
12
9
8
（1）分析表中数据，请从一次函数和反比例函数中确定一个函数表示其变化规律，求出y与x的函数关系式，并说明理由；
（2）若2022年公司打算投入技术改进资金5万元，预计2022年产品成本比2021年降低多少万元？
（3）若2023年公司打算把投入技术改进资金x和产品成本y之和控制在12万元，请分别求出投入技术改进资金和产品成本．
【分析】（1）利用已知数据可得横纵坐标的积为定值，进而得出答案；
（2）利用所求函数解析式进而利用x＝6时求出y的值即可得出答案；
（3）结合（1）的关系式列方程组解答即可．
【解答】解：（1）根据已知数据可得：xy＝36，
∴y与x的函数关系式是：y＝；
（2）当x＝5时，y＝＝7.2，
则8﹣7.2＝0.8（万元），
答：预计2022年产品成本比2021年降低0.8万元；
（3）由题意，
得，
解得，
答：投入技术改进资金为6万元，产品成本为6万元．
【点评】此题主要考查了反比例函数的应用，正确得出反比例函数解析式是解题关键．
23．（12分）在正方形ABCD中，点E、F分别是边AD和DC上一点，且DE＝DF，连结CE和AF，点G是射线CB上一点，连结EG，满足EG＝EC，AF交EG于点M，交EC于点N．
（1）证明：∠DAF＝∠DCE；
（2）求线段EG与线段AF的关系（位置与数量关系），并说明理由；
（3）是否存在实数m，当AM＝mAF时，BC＝3BG？若存在，请求出m的值；若不存在，请说明理由．

【分析】（1）根据正方形的性质得到对应边相等，证明△ADF≌△CDE即可得到∠DAF＝∠DCE；
（2）作BH∥EG，交AF于点K，交AD于点H，则BH＝EG，通过证明△ABH≌△DAF，得到∠ABH＝∠DAF，可推导出∠AMG＝90°，从而证得结论；
（3）存在，作EL⊥BC于点L，连结EF，分两种情况，即点G在BC边上、点G在CB边的延长线上，分别设BG＝a和BG＝n，将AE、DE、DF用a或n表示出来，再将AF、AM用a或n表示出来，即可求出m的值．
【解答】（1）证明：如图1，∵四边形ABCD是正方形，
∴AD＝CD，
∵∠D＝∠D，DE＝DF，
∴△ADF≌△CDE（SAS），
∴∠DAF＝∠DCE．
（2）EG⊥AF，EG＝AF，理由如下：
如图2（或图3），作BH∥EG，交AF于点K，交AD于点H，
∵AD∥BC，
∴EH∥BG，
∴四边形BGEH是平行四边形，
∴BH＝EG；
由（1）得，△ADF≌△CDE，
∴AF＝EC，
∵EG＝EC，
∴EG＝AF，BH＝AF，
∵BA＝AD，∠BAH＝∠D＝90°，
∴Rt△ABH≌Rt△DAF（HL），
∴∠ABH＝∠DAF，
∴∠ABH+∠BAK＝∠DAF+∠BAK＝∠BAD＝90°，
∴∠AKB＝90°，
∴∠AMG＝∠AKB＝90°，
∴EG⊥AF，
∴EG⊥AF，EG＝AF．
（3）存在，作EL⊥BC于点L，连结EF，
∵∠ELC＝∠LCD＝∠D＝90°，
∴四边形ELCD是矩形，
∴CL＝DE，
∴CL＝DE＝DF，
如图4，点G在边BC上，设CL＝DE＝DF＝a，
∵EG＝EC，
∴CL＝GL，
∵BC＝3BG，
∴CG＝2BG＝2CL＝2GL，
∴BG＝CL＝GL，
∴AD＝BC＝3a，
∴AE＝2a，
∴AF＝＝a，
∵EG⊥AF，
∴∠AMF＝90°，
由AF•EM＝AE•DF＝S△AEF得，AF•EM＝AE•DF，
∴a•EM＝2a•a，
∴EM＝a，
∴AM＝＝，
∵AM＝mAF，
∴m＝＝＝；
如图5，点G在边CB的延长线上，设BG＝n，
则AD＝BC＝3n，
∴CG＝4n，
∴CL＝DE＝DF＝CG＝2n，
∴AF＝＝n，AE＝3n﹣2n＝n，
由AF•EM＝AE•DF得，n•EM＝2n•n，
∴EM＝n，
∴AM＝＝，
∴m＝＝＝，
综上所述，m＝或m＝．




【点评】此题重点考查正方形的性质、平行四边形的判定与性质、全等三角形的判定与性质、勾股定理以及二次根式等知识，第（3）题要分类讨论，求出所有符合条件的值，此题难度较大，属于考试压轴题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/9/1 12:19:24；用户：初中数学；邮箱：hzjf555@xyh.com；学号：24117474