2021-2022学年浙江省宁波市精准联盟八年级（下）期中数学试卷（含解析）

这是一份2021-2022学年浙江省宁波市精准联盟八年级（下）期中数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题（本大题共10小题，共40分）
要使二次根式x−2有意义，x的值可以是( )
A. 2B. 1C. 0D. −1
下列图案中，既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
下列计算正确的是( )
A. (−5)2=−5B. 53⋅52=56
C. 310−25=5D. 72=7
用配方法解方程x2+4x−5=0，下列配方正确的是( )
A. (x+2)2=1B. (x+2)2=5C. (x+2)2=9D. (x+4)2=9
若n边形的内角和与外角和相加为1800°，则n的值为( )
A. 7B. 8.C. 9D. 10
用反证法证明三角形至少有一个角不大于60°，应假设( )
A. 三个角都小于60°B. 三个角都大于60°
C. 三个角都大于或等于60°D. 有两个角大于60°
某海鲜市场以每千克10元的进价进了一批螃盤，经市场调研发现：售价为每千克20元时，每天可销售40千克．售价每上涨1元，每天的销量将减少3千克．如果该海鲜市场想平均每天获利408元，设这种螃蟹的售价上涨了x元，根据题意可列方程为( )
A. (x−10)[40−3(x−20)]=408B. (20+x)(40−3x)−10×40=408
C. (20+x)(40−3x)=408D. (20+x−10)(40−3x)=408
在四边形ABCD中，AC、BD交于点O，在下列条件中，不能判定四边形ABCD为矩形的是( )
A. AO=CO，BO=DO，∠BAD=90°
B. AB=CD，AD=BC，AC=BD
C. ∠BAD=∠BCD，∠ABC+∠BCD=180°，AC⊥BD
D. ∠BAD=∠ABC=90°，AC=BD
如图，将平行四边形ABCD沿对边上两点连线EF对折，使点A恰好落在点C处，若∠ABC=120°，AD=4，AB=8，则AE的长为( )
A. 4.6
B. 43
C. 5.6
D. 53
如图，①②③④⑤五个平行四边形拼成一个含45°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为142cm2，四边形ABCD面积是112cm2，则①②③④四个平行四边形周长的总和为( )
A. 48B. 24C. 482D. 242
二、填空题（本大题共6小题，共30分）
点(−4,3)关于原点对称的点的坐标是______．
甲、乙、丙、丁四名同学进行跳高测试，每人10次跳高成绩的平均数都是1.28m，方差分别是S甲2=0.63m2，S乙2=0.61m2，S丙2=0.57m2，S丁2=0.56m2，则这四名同学成绩最稳定的是______．
如果y=x−2+2−x+5，那么yx的值是______．
目前以5G等为代表的战略性新兴产业蓬勃发展.某市2020年底有5G用户2万户，计划到2022年底全市5G用户数累积到达到9.5万户.设全市5G用户数年平均增长率为x，则x的值为______ ．
如图，在▱ABCD中，AB=10，BC=18，∠ABC和∠BCD的角平分线分别交AD于点E和F，若BE=12，则CF=______．
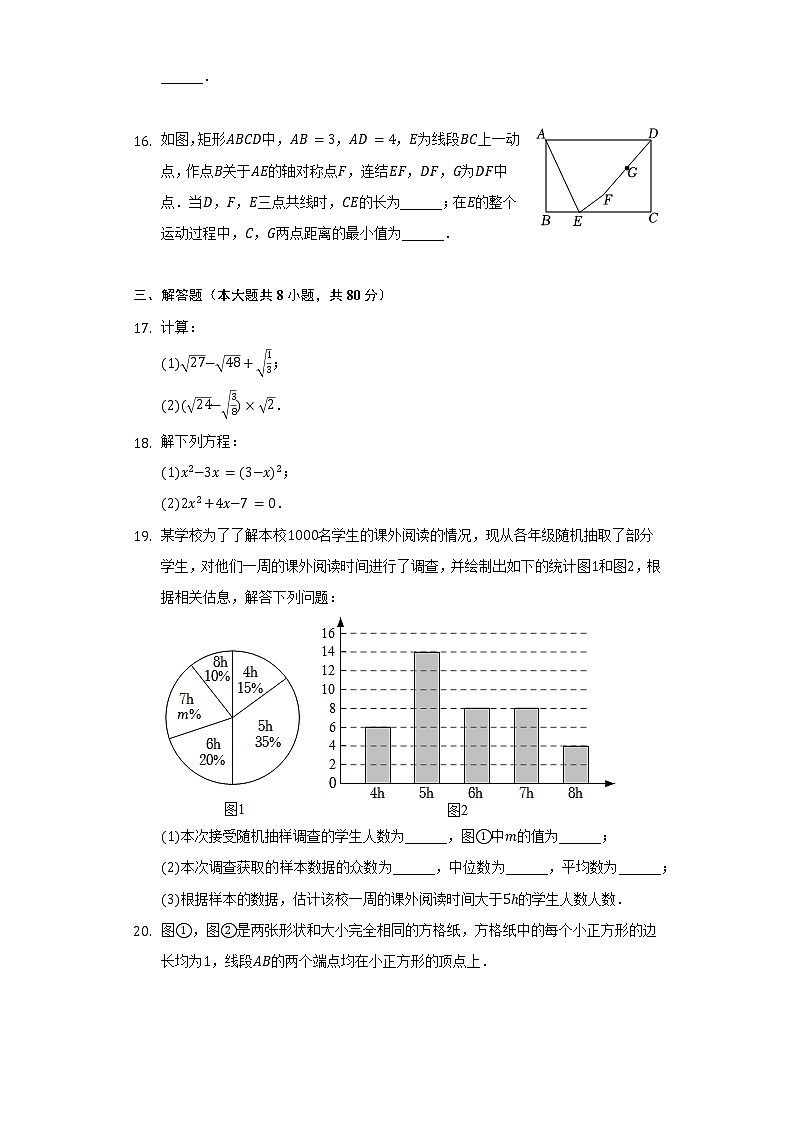
如图，矩形ABCD中，AB=3，AD=4，E为线段BC上一动点，作点B关于AE的轴对称点F，连结EF，DF，G为DF中点．当D，F，E三点共线时，CE的长为______；在E的整个运动过程中，C，G两点距离的最小值为______．
三、解答题（本大题共8小题，共80分）
计算：
(1)27−48+13；
(2)(24−38)×2．
解下列方程：
(1)x2−3x=(3−x)2；
(2)2x2+4x−7=0．
某学校为了了解本校1000名学生的课外阅读的情况，现从各年级随机抽取了部分学生，对他们一周的课外阅读时间进行了调查，并绘制出如下的统计图1和图2，根据相关估息，解答下列问题：
(1)本次接受随机抽样调查的学生人数为______，图①中m的值为______；
(2)本次调查获取的样本数据的众数为______，中位数为______，平均数为______；
(3)根据样本的数据，估计该校一周的课外阅读时间大于5ℎ的学生人数人数．
图①，图②是两张形状和大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．
(1)请在图①中画一个以A.B为顶点，面积为6的平行四边形(非矩形)，点C，D在格点上．
(2)请在图②中画一个以A，B为顶点，面积为6的矩形，点C，D在格点上．
已知：关于x的一元二次方程x2−2mx+m2−1=0．
(1)判断方程的根的情况；
(2)若△ABC为等腰三角形，AB=5cm，另外两条边长是该方程的根，求△ABC的周长．
如图，菱形ABCD的对角线AC和BD交于点O，分别过点C.D作CE//BD，DE//AC，CE和DE交于点E．
(1)求证：四边形ODEC是矩形；
(2)当∠ADB=60°，AB=10时，求CE和AE的长．
园林部门计划在某公园建一个长方形苗圃ABCD.苗圃的一面靠墙(墙最大可用长度为14米).另三边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并在如图所示的两处各留2米宽的门(门不用木栏)，建成后所用木栏总长32米，设苗圃ABCD的一边CD长为x米．
(1)BC长为______米(包含门宽，用含x的代数式表示)；
(2)若苗圃ABCD的面积为96m2，求x的值；
(3)当x为何值时，苗圃ABCD的面积最大，最大面积为多少？
问题原型：
(1)如图1，在菱形ABCD中，∠B=60°，AE⊥BC于E，F为CD中点，连结AF，EF.试猜想△AEF的形状，并说明理由．
弱化演变：
(2)如图2，在▱ABCD中，AE⊥BC于E，F为CD中点，连结AF，EF.试猜想△AEF的形状，并说明理由．
拓展演变：
(3)如图3，在▱ABCD中，F为CD上一点，连结BF，将∠C沿BF折叠，点C的对应点为C′.连结DC′并延长交AB于G，若AG=C′F，求证：F为CD中点．
组合演变：
(4)如图4，直角坐标系中有▱ABCD，点A与原点重合，点B在x轴正半轴上，CD与y轴交于点E.将其沿过A的直线折叠，点B对应点B′恰好落在y轴上，且折痕交BC于M，B′M交CD于点N.若▱ABCD的面积为48，AB=8，AD=35，求点M的坐标和阴影部分面积(直接写出结果)．
答案和解析
1.【答案】A
【解析】解：由题意可知：x−2≥0，
∴x≥2，
故选：A．
根据二次根式有意义的条件即可求出答案．
本题考查二次根式，解题的关键是正确理解二次根式有意义的条件，本题属于基础题型．
2.【答案】B
【解析】解：A.不是中心对称图形，是轴对称图形，故此选项不合题意；
B.既是中心对称图形，也是轴对称图形，故此选项符合题意；
C.是中心对称图形，不是轴对称图形，故此选项不合题意；
D.是中心对称图形，不是轴对称图形，故此选项不合题意；
故选：B．
根据中心对称图形与轴对称图形的概念进行判断即可．
本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．
3.【答案】D
【解析】解：A、原式=5，故A不符合题意．
B、原式=256，故B不符合题意．
C、310与−25不是同类二次根式，不能合并，故C不符合题意．
D、原式=7，故D符合题意．
故选：D．
根据二次根式的加减运算以及乘除运算法即可求出答案．
本题考查二次根式的混合运算，解题的关键是熟练运用二次根式的加减运算以及乘除运算，本题属于基础题型．
4.【答案】C
【解析】解：x2+4x−5=0，
配方，得
(x+2)2=9．
故选：C．
先将原方程进行配方，然后选项进行对照，即可得到正确选项．
本题考查解一元二次方程---配方法，解题的关键是学生明确什么是配方法、如何运用配方法对一元二次方程配方．
5.【答案】D
【解析】解：由题意得，180°×(n−2)+360°=1800°，
解得：n=10，
故选：D．
先求得多边形的内角和，然后根据条件列出方程，即可求得n的值．
本题考查了多边形的内角和公式和外角和定理，解题的关键是熟练应用多边形的内角和公式列出方程．
6.【答案】B
【解析】解：反证法证明三角形至少有一个角不大于60°，
应假设三个角都大于60°，
故选：B．
根据反证法的步骤中，第一步是假设结论不成立，反面成立解答．
本题考查的是反证法的应用，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
7.【答案】D
【解析】解：设这种螃蟹的售价上涨了x元，则每千克的销售利润为(20+x−10)元，每天可销售(40−3x)千克，
依题意得：(20+x−10)(40−3x)=408．
故选：D．
设这种螃蟹的售价上涨了x元，则每千克的销售利润为(20+x−10)元，每天可销售(40−3x)千克，利用每天的销售利润=每千克的销售利润×每天的销售量，即可得出关于x的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
8.【答案】C
【解析】解：A、∵AO=CO，BO=DO，
∴四边形ABCD是平行四边形，
又∵∠BAD=90°，
∴平行四边形ABCD是矩形，故选项A不符合题意；
B、∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形，
又∵AC=BD，
∴平行四边形ABCD是矩形，故选项B不符合题意；
C、∵∠ABC+∠BCD=180°，
∴AB//CD，
∵∠BAD=∠BCD，
∴∠ABC+∠BAD=180°，
∴AD//BC，
∴四边形ABCD是平行四边形，
又∵AC⊥BD，
∴平行四边形ABCD是菱形，故选项C符合题意；
D、∵∠BAD=∠ABC=90°，
∴AD//BC，
在Rt△ABD和Rt△BAC中，
AB=BABD=AC，
∴Rt△ABD≌Rt△BAC(HL)，
∴AD=BC，
∴四边形ABCD是平行四边形，
又∵AC=BD，
∴平行四边形ABCD是矩形，故选项D不符合题意；
故选：C．
由平行四边形的判定与性质、矩形的判定以及菱形的判定分别对各个选项进行判断即可．
本题考查了平行四边形的判定与性质、矩形的判定、菱形的判定以及全等三角形的判定与性质等知识，熟练掌握矩形的判定和菱形的判定是解题的关键．
9.【答案】C
【解析】解：如图，过点C作CG⊥AB的延长线于点G，

∵四边形ABCD为平行四边形，∠ABC=120°，AD=4，AB=8，
∴∠CBG=60°，BC=AD=4，
∴BG=12BC=2，CG=32BC=23，
设AE=x，
∴BE=AB−AE=8−x，
∴EG=BE+BG=10−x，
∵平行四边形ABCD沿对边上两点连线EF对折，
∴CE=AE=x，
在Rt△CEG中，由勾股定理可得：
EG2+CG2=CE2，
即(10−x)2+(23)2=x2，
解得：x=5.6，
∴AE的长为5.6，
故选：C．
过点C作CG⊥AB的延长线于点G，根据平行四边形的性质可得BC，再由30°角的直角三角形可得BG，CG，设AE为x，可得BE=8−x，由折叠性质可得CE=AE，在Rt△CEG中，由勾股定理可求出x，即可求解．
本题考查折叠的性质，平行四边形的性质等知识点，解题的关键是正确作出辅助线，利用勾股定理求解．
10.【答案】A
【解析】解：作GM⊥EF于点M．

由题意得：S⑤=S四边形ABCD−12(S①+S②+S③+S④)=112−12×142=42cm2，
∴S菱形EFGH=142+42=182cm2，
又∵∠F=45°，
设菱形的边长为x，则菱形的高为：GM=22GF=22x，
根据菱形的面积公式得：x⋅2x2=182，
解得：x=6，
∴菱形的边长为6cm，
而①②③④四个平行四边形周长的总和=2(AE+AH+HD+DG+GC+CF+FB+BE)=2(EF+FG+GH+HE)=48cm．
故选：A．
根据①②③④四个平行四边形面积的和为142cm2，四边形ABCD面积是112cm2，可求出⑤的面积，从而可求出菱形的面积，根据菱形的性质可求出边长，进而可求出①②③④四个平行四边形周长的总和．
本题考查了菱形的性质及平行四边形的性质．此题难度较大，注意数形结合思想与方程思想的应用．
11.【答案】(4,−3)
【解析】解：根据关于原点对称的点的坐标的特点，
∴点(−4,3)关于原点对称的点的坐标是(4,−3)．
故答案为(4,−3)．
平面直角坐标系中任意一点P(x,y)，关于原点的对称点是(−x,−y)，即关于原点的对称点，横纵坐标都变成相反数．
本题主要考查了平面直角坐标系中任意一点P(x,y)，关于原点的对称点是(−x,−y)，即关于原点的对称点，横纵坐标都变成相反数，比较简单．
12.【答案】丁
【解析】解：∵S甲2=0.63m2，S乙2=0.61m2，S丙2=0.57m2，S丁2=0.56m2，
∴S丁2∴这四名同学成绩最稳定的是丁，
故答案为：丁．
根据方差的意义求解即可．
本题主要考查方差，解题的关键是掌握方差的意义：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越差；反之，则它与其平均值的离散程度越小，稳定性越好．
13.【答案】25
【解析】解：∵x−2≥0，2−x≥0，
∴x=2，
∴y=5，
∴yx=52=25．
故答案为：25．
根据二次根式的被开方数是非负数求出x的值，进而得到y的值，代入代数式求值即可得出答案．
本题考查了二次根式有意义的条件，掌握二次根式的被开方数是非负数是解题的关键．
14.【答案】120%
【解析】解：设全市5G用户数年平均增长率为x，
依题意，得：2(1+x)2=9.5，
解得：x1≈1.2=120%，x2≈−3.2(不合题意，舍去)．
故答案为：120%．
设全市5G用户数年平均增长率为x，根据该市2020年底及计划到2022年底全市5G用户数量，即可得出关于x的一元二次方程，解之取其正值即可得出结论．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
15.【答案】16
【解析】解：如图，设BE与FC的交点为H，过点A作AM//FC，交BE与点O，

∵四边形ABCD是平行四边形，
∴AD//BC，AB//CD，
∴∠ABC+∠DCB+180°，
∵BE平分∠ABC，CF平分∠BCD，
∴∠ABE=∠EBC，∠BCF=∠DCF，
∴∠CBE+∠BCF=90°，
∴∠BHC=90°，
∵AM//CF，
∴∠AOE=∠BHC=90°，
∵AD//BC，
∴∠AEB=∠EBC=∠ABE，
∴AB=AE=10，
又∵∠AOE=90°，
∴BO=OE=6，
∴AO=AE2−EO2=102−62=8，
在△ABO和△MBO中，
∠ABO=∠CBOBO=BO∠AOB=∠MOB=90°，
∴△ABO≌△MBO(ASA)，
∴AO=OM=8，
∴AM=16，
∵AD//BC，AM//CF，
∴四边形AMCF是平行四边形，
∴CF=AM=16，
故答案为：16．
过点A作AM//FC，交BE与点O，由平行线的性质和角平分线的性质可证∠BHC=90°，由平行线的性质可求∠AOE=∠BHC=90°，由平行线的性质和角平分线的性质可证AE=AB=10，由勾股定理可求AO的长，由“ASA”可证△ABO≌△MBO，可得AO=OM，通过证明四边形AMCF是平行四边形，可得CF=AM．
本题考查了平行四边形的性质，等腰三角形的判定和性质，添加恰当辅助线构造平行四边形是解题的关键．
16.【答案】7 13−32
【解析】解：如图，连接AF，

∵点B关于AE的轴对称点F，
∴AF=AB=3，BE=BF，
在Rt△ABE和Rt△AFE中，
AB=AFAE=AEBE=EF，
∴Rt△ABE≌Rt△AFE(SSS)，
∴∠B=∠AFE=90°，
当D，F，E三点共线时，∠AFD=90°，
∴DF=AD2−AF2=16−9=7，
∵DE2=CD2+CE2，
∴(7+BE)2=9+(4−BE)2，
∴BE=94+7=4−7，
∴CE=7，
如图，取AD的中点H，连接GH，CG，CH，

∵AD=4，点H是AD中点，
∴DH=2，
∴CH=DH2+CD2=4+9=13，
∵点H是AD中点，点G是DF中点，
∴HG=12AF=32，
在△HGC中，CG>CH−HG，
∴当点G在CH上时，CG有最小值为：13−32，
故答案为：7，13−32．
由轴对称的性质和全等三角形的性质可求∠AFD=90°，AF=AB=3，BE=BF，由勾股定理可求DF，BE的长，即可求CE的长，取AD的中点H，连接GH，CG，CH，由三角形的三边关系可求解．
本题考查了矩形的性质，全等三角形的判定和性质，轴对称的性质，勾股定理等知识，灵活运用这些性质解决问题是解题的关键．
17.【答案】解：(1)27−48+13
=33−43+33
=−233；
(2)(24−38)×2
=(26−64)×2
=764×2
=732．
【解析】(1)先化简，再算加减即可；
(2)先化简，再算减法，最后算乘法即可．
本题主要考查二次根式的混合运算，解答的关键是对相应的运算法则的掌握．
18.【答案】解：(1)x2−3x=(3−x)2，
x2−3x=9−6x+x2，
6x−3x=9，
3x=9，
所以x=3；
(2)2x2+4x−7=0，
x2+2x=72，
x2+2x+1=92，
(x+1)2=92，
x+1=±322，
所以x1=−1+322，x2=−1−322．
【解析】(1)先去括号，然后移项、合并，最后把x的系数化为1即可；
(2)利用配方法得到(x+1)2=92，然后利用直接开平方法解方程．
本题考查了解一元二次方程−因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了配方法．
19.【答案】40 20 5 6 5
【解析】解：(1)接受随机抽样调查的学生人数：4÷10%=40(人)，
m%=8÷40×100%=20%，
则m=20，
故答案为：40；20；
(2)本次调查获取的样本数据的众数是5小时，中位数是6小时，
平均数为：140×(4×6+5×14+6×8+7×8+8×4)=5(小时)，
故答案为：5；6；5；
(3)1000×(20%+20%+10%)=500(人)，
答：该校一周的课外阅读时间大于5ℎ的学生人数为500人．
(1)利用课外阅读时间为8小时的人数除以所占百分比可得本次接受随机抽样调查的学生人数，然后再求m的值即可；
(2)根据众数、中位数和平均数的定义可得答案；
(3)利用样本估计总体的方法可得答案．
本题主要考查众数、中位数、平均数、扇形统计图和条形统计图的知识，解题的关键是能结合两图找出关键信息．
20.【答案】解：(1)如图①中，四边形ACBD即为所求；
(2)如图②中，矩形ADBC即为所求．
【解析】(1)作一个底为3，高为2的平行四边形即可；
(2)作一个长宽分别为2，32的矩形即可．
本题考查作图−应用与设计作图，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
21.【答案】解：(1)∵Δ=(−2m)2−4(m2−1)=4>0，
∴方程有两个不相等的实数根；
(2)x=2m±22=m±1，
∴x1=m+1，x2=m−1，
当m+1=5时，解得m=4，此时等腰三角形三边分别为5，5，3，△ABC的周长为5+5+3=13；
当m−1=5时，解得m=6，此时等腰三角形三边分别为5，5，7，△ABC的周长为5+5+7=17；
综上所述，△ABC的周长为13或17．
【解析】(1)先计算根的判别式的值得到△=4>0，然后根据根的判别式的意义判断方程根的情况；
(2)先利用求根公式解方程得到x1=m+1，x2=m−1，根据等腰三角形的性质讨论：当m+1=5时，解得m=4，此时等腰三角形三边分别为5，5，3；当m−1=5时，解得m=6，此时等腰三角形三边分别为5，5，7，然后分别计算对应的三角形的周长．
本题考查了根的判别式：一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：当Δ>0时，方程有两个不相等的实数根；当Δ=0时，方程有两个相等的实数根；当Δ<0时，方程无实数根．也考查了三角形三边的关系和等腰三角形的性质．
22.【答案】(1)证明：∵CE//BD，DE//AC，
∴四边形ODEC是平行四边形．
又∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠DOC=90°．
∴四边形ODEC是矩形；
(2)解：∵四边形ABCD是菱形，
∴AD=AB=10，OA=OC，
在Rt△AOD中，∠ADO=60°，
∴∠DAO=30°，
∴OD=12AD=5，
∴OA=AD2−OD2=102−52=53，
∴AC=103，
∵四边形ODEC是矩形，
∴CE=OD=5，∠ACE=90°，
在Rt△AOD中，
AE=CE2+AC2=52+(103)2=25．
【解析】(1)先证四边形ODEC是平行四边形，然后根据菱形的对角线互相垂直，得到∠DOC=90°，根据矩形的定义即可判定四边形ODEC是矩形；
(2)根据含30度角直角三角形的性质和勾股定理求出CE，AC，根据勾股定理即可求出EA的长度．
本题考查了菱形的性质，矩形的判定与性质，勾股定理的应用，是基础题，熟记矩形的判定方法与菱形的性质是解题的关键．
23.【答案】(36−3x)
【解析】解：(1)∵木栏总长32米，两处各留2米宽的门，设苗圃ABCD的一边CD长为x米，
∴BC长为32−3x+4=36−3x，
故答案为：(36−3x)；
(2)根据题意得：x⋅(36−3x)=96，
解得x=4或x=8，
∵x=4时，36−3x=24>14，
∴x=4舍去，
∴x的值为8；
(3)设苗圃ABCD的面积为w，
则w=x⋅(36−3x)=−3x2+36x=−3(x−6)2+108，
∵−3<0，
∴x=6时，w最大为108，
答：当x为6米时，苗圃ABCD的最大面积为108平方米．
(1)根据木栏总长32米，两处各留2米宽的门，设苗圃ABCD的一边CD长为x米，即得BC长为(36−3x)米；
(2)根据题意得：x⋅(36−3x)=96，即可解得x的值；
(3)w=x⋅(36−3x)=−3(x−6)2+108，由二次函数性质可得答案．
本题考查二次函数的应用，解题得关键是读懂题意，根据已知列方程和函数关系式．
24.【答案】(1)解：如图1，

连接AC，
∵四边形ABCD是菱形，
∴AD=BC=AB，
∵∠B=60°，
∴△ABC是等边三角形，
∴AC=AB，∠BAC=60°，
∵AE⊥BC，
∴∠CAE=∠BAE=12∠BAC=30°，
同理可得：△ACD是等边三角形，
∴AD=AC，∠DAC=60°，
∵点F是CD的中点，
∴∠CAF=12∠DAC=30°，AF⊥CD，
∴∠EAF=∠CAE+∠CAE=60°，
在△ADF和△ABE中，
∠D=∠B∠AFD=∠AEB=90°AD=AB，
∴△ADF≌△ABE(AAS)，
∴AF=AE，
∴△AEF是等边三角形；
(2)解：如图2，

△AEF是等腰三角形，理由如下：
取AB的中点，连接FH，直线FH交AE于G，
∵四边形ABCD是平行四边形，
∴AB//CD，AB=CD，
∵点F是CD的中点，H是AB的中点，
∴CF=12CD,BH=12AB，
∴BH=CF，
∴四边形BCFH是平行四边形，
∴FG//CE，
∴点G是AE的中点，
∵AE⊥CE，
∴FG⊥AE，
∴AE=AF，
即：△AEF是等腰三角形；
(3)证明：由(2)知：AB=CD，AB//CD，
∵AG=C′F，CF=C′F，
∴AG=CF，
∴CD=CF=AB−AG，
∴CF=BG，
∴四边形BGDF是平行四边形，
∴BF//DG，
∴∠FDC′=∠CFB，∠C′FB=∠DC′F，
∵∠CFB=∠C′FB，
∴∠FDC′=∠DC′F，
∴DF=C′F，
∴DF=CF，
即：点F是CD的中点
(4)解：由S平行四边形ABCD=AB⋅AE得，
8AE=48，
∴AE=6，
∵四边形ABCD是平行四边形，
∴AB//CD，CD=AB=8，
∵∠EAB=90°，
∴∠AED=∠EAB=90°，
∴DE=AD2−AE2=(35)2−62=3，
∴CE=CD−DE=5，
∴C(5,6)，
∴直线BC的解析式为：y=−2x+16，
∵∠BAM=∠CAE=12∠BAE =45°，
∴直线AM的解析式为：y=x，
由x=−2x+16得，
x=163，
∴M(163,163)，
∵AB′=AB=8，
∴B′(0,8)，
∴直线MN的解析式为：y=−12x+8，
当y=6时，6=−12x+8，
∴x=4，
∴EN=4，
∴S△ENB′=12EB′⋅EN=12×2×4=4，
∵S△AMB′=12×8×163=643，
∴S阴影=643−4=523．
【解析】(1)连接AC，证明△ABC和△ACD是等边三角形，进而证明∠EAF=60°，证明△ADF≌△ABE，从而得出AE=AF，进而得出结果；
(2)取AB的中点，连接FH，直线FH交AE于G，证明四边形BCFH是平行四边形，FG//CE，进而得出GH是△ABE的中位线，进一步得出△AEF是等腰三角形；
(3)由条件推出CF=BG，进而得出四边形BGDF是平行四边形，从而BF//DG，进而证明∠FDC′=∠DC′F，进一步得出结论；
(4)根据条件求得DE=3，CE=5，从而求得BC的解析式，求出AM的解析式，从而求得点M坐标，求出MN的解析式，从而求得N点坐标，从而求得EN的长，求出△AMB′和△ENB′的面积，进而求得阴影部分面积．
本题考查了菱形性质，平行四边形性质，等腰三角形的判定，勾股定理，求一次函数解析式等知识，解决问题的关键是作辅助线，构造线段垂直平分线．
题号
一
二
三
总分
得分