2021-2022年度北京市海淀区八年级第二学期数学期末模拟卷

这是一份2021-2022年度北京市海淀区八年级第二学期数学期末模拟卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

考生须知：
本试卷分试题卷和答题卷两部分，满分150分，考试试卷120分钟。
答题前，必须在答题卡上填写校名，班级，姓名，座位号。
不允许使用计算器进行计算，凡题目中没有要求取近似值的，结果应保留根号或π
一、选择题（每小题3分，有10小题，共30分。）
1．设a＞0，b＞0，则下列运算中错误的是（ ）
A．ab=a·bB．a+b=a+bC．a2=aD．ab=ab
2．下列各组数中，以a、b、c为边的三角形不是直角三角形的是 （ ）
A．a=1.5，b=2，c=3B．a=7，b=24，c=25
C．a=6，b=8，c=10D．a=3，b=4，c=5
3．将直线 y=x+1 向右平移2个单位长度，可得直线的解析式为（ ）
A．y=x-3B．y=x-1C．y=x+3D．y=x+1
4．△ABC中，∠B=50°，∠A=80°，若AB=6，则AC=（ ）
A．6B．8C．5D．13
5．某体育用品商店对某一型号运动服9月份的销售情况的统计如图所示，店长决定下个月进该型号运动服时多进一些蓝色的，店长的这一决定主要参考销售数据中的（ ）
A．平均数B．方差C．中位数D．众数
6．如图，P为边长为2的等边三角形ABC内任意一点，连接PA、PB、PC，过P点分别作BC、AC、AB边的垂线，垂足分别为D、E、F，则PD+PE+PF等于（ ）
A．32B．3C．2D．23
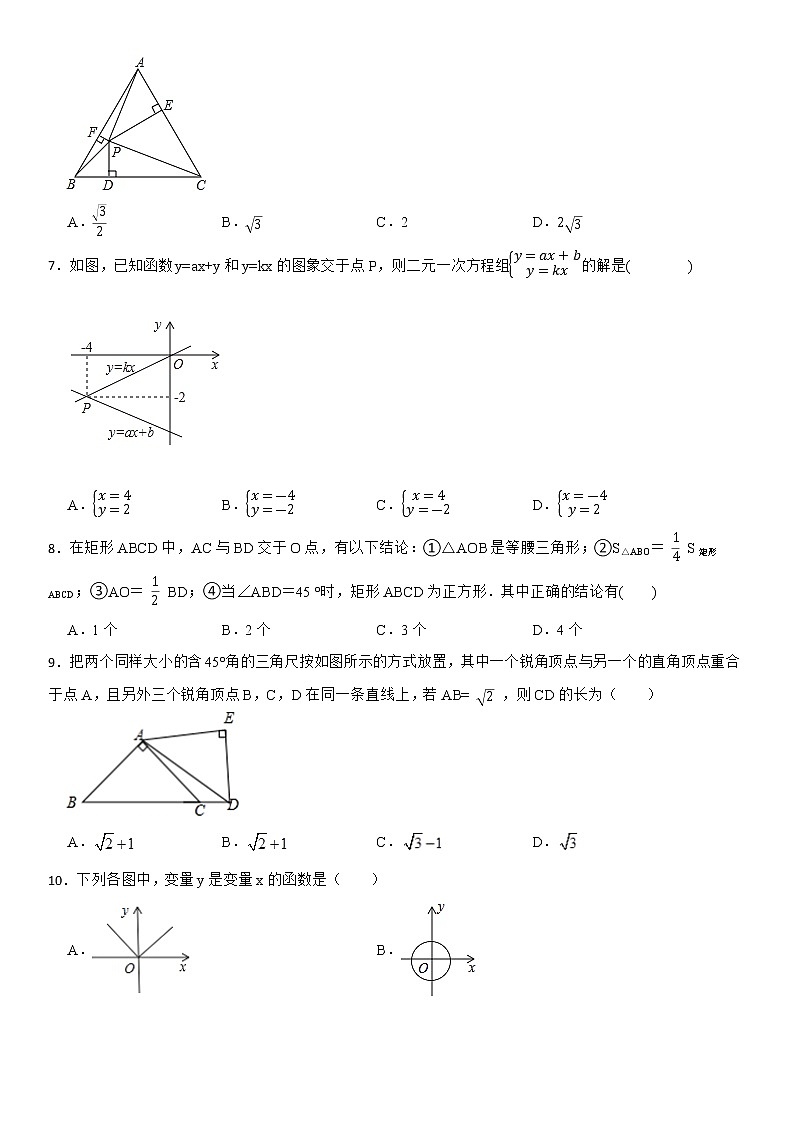
7．如图，已知函数y=ax+y和y=kx的图象交于点P，则二元一次方程组y=ax+by=kx的解是( )
A．x=4y=2B．x=-4y=-2C．x=4y=-2D．x=-4y=2
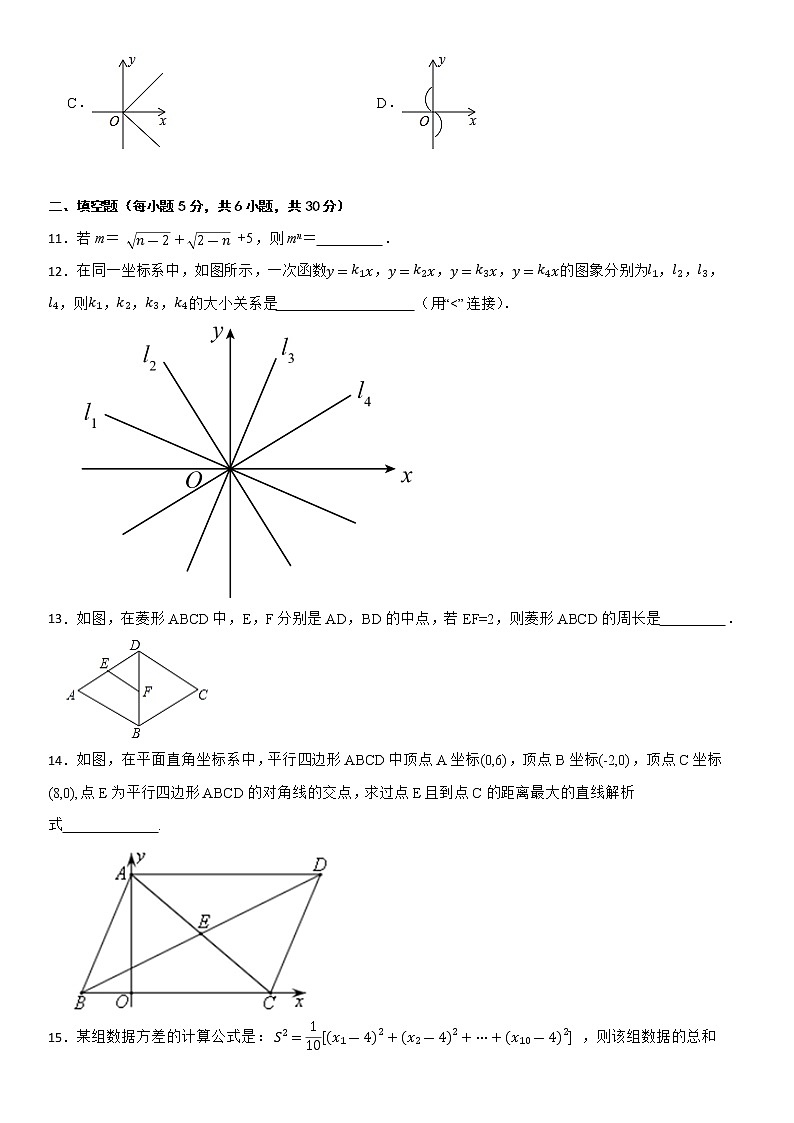
8．在矩形ABCD中，AC与BD交于O点，有以下结论：①△AOB是等腰三角形；②S△ABO＝ 14 S矩形ABCD；③AO＝ 12 BD；④当∠ABD＝45 °时，矩形ABCD为正方形．其中正确的结论有( )
A．1个B．2个C．3个D．4个
9．把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个锐角顶点与另一个的直角顶点重合于点A，且另外三个锐角顶点B，C，D在同一条直线上，若AB= 2 ，则CD的长为（ ）
A．B．C．D．
10．下列各图中，变量y是变量x的函数是（ ）
A．B．
C．D．
二、填空题（每小题5分，共6小题，共30分）
11．若m＝ n-2+2-n +5，则mn＝ ．
12．在同一坐标系中，如图所示，一次函数y=k1x，y=k2x，y=k3x，y=k4x的图象分别为l1，l2，l3，l4，则k1，k2，k3，k4的大小关系是 （用“<”连接）．
13．如图，在菱形ABCD中，E，F分别是AD，BD的中点，若EF=2，则菱形ABCD的周长是 ．
14．如图，在平面直角坐标系中，平行四边形ABCD中顶点A坐标(0,6)，顶点B坐标(-2,0)，顶点C坐标(8,0),点E为平行四边形ABCD的对角线的交点，求过点E且到点C的距离最大的直线解析式 .
15．某组数据方差的计算公式是： S2=110[(x1-4)2+(x2-4)2+⋅⋅⋅+(x10-4)2] ，则该组数据的总和为 .
16．一个水库的水位在最近5h内持续上涨，下表记录了这5h内6个时间点的水位高度，其中t表示时间，y表示水位高度．
据估计这种上涨规律还会持续2h，预测再过2h水位高度将为 m．
三、解答题（共9题，共90分。解答应写出文字说明、证明过程或演算步骤）
17．
（1）(26+35)(26-35) ；
（2）8+313-12+32
18．如图，O是平行四边形ABCD对角线的交点，过点O的直线EF分别交AD、BC于F、E两点．求证：四边形AECF是平行四边形．
19．读下列语句，并画出图形：
直线AB、CD是相交直线，点P是直线AB，CD外一点，直线EF经过点P，且与直线AB平行，与直线CD相交于点E．
20．定义：关于x的一次函数y＝ax+b与y＝bx+a（ab≠0）叫做一对交换函数，例如：一次函数y＝3x+4与y＝4x+3就是一对交换函数．
（1）一次函数y＝2x﹣b的交换函数是 ；
（2）当b≠﹣2时，（1）中两个函数图象交点的横坐标是 ；
（3）若（1）中两个函数图象与y轴围成的三角形的面积为4，求b的值．
21．如图，在 ▱ABCD 中， AE 平分 ∠BAD ，交 BC 于点 E ， BF 平分 ∠ABC ，交 AD 于点 F . AE 与 BF 交于点 P ，连接 EF ， PD .
（1）求证：四边形 ABEF 是菱形；
（2）若 AB=6 ， AD=9 ， ∠ABC=60° ，求 ∠DCP 的度数.
22．在一次广场舞比赛中，甲、乙两个队参加表演的女演员的身高（单位：cm）分别是甲队：163 165 165 164 168
乙队：162 164 164 167 168
（1）求甲队女演员身高的平均数、中位数﹑众数；
（2）计算两队女演员身高的方差，并判断哪个队女演员的身高更整齐？
23．已知直线y=kx+b（k≠0）过点（1，2）
（1）填空：b= （用含k代数式表示）；
（2）将此直线向下平移2个单位，设平移后的直线交x于点A，交y于点B，x轴上另有点C（1+k，0），使得△ABC的面积为2，求k值；
（3）当1≤x≤3，函数值y总大于零，求k取值范围.
24．已知：如图所示，在 △ABC 中， D 是 AC 的中点， E 是线段 BC 的延长线上一点，过点 A 作 AF 平行 BE ，交线段 ED 的延长线于点 F ，连接 AE､CF .
（1）求证： AF=CE ；
（2）若 AF=CF=4,∠AFD=30° ，求 EF 的长.
25．如图，P为正方形 ABCD 对角线 AC 上的一点，连接 DP 并延长交 AB 于点E，过P作 MN⊥DE 分别交 BC ， AD 于M，N．
（1）如图1，求证： MN=DE ；
（2）如图2，点F与点C关于直线 DE 对称，连接 FA 并延长交直线 DE 于点G，连接 BG ．
①设 ∠ADE 的度数为x，求 ∠DGF 的度数：
②猜想 AF 与 BG 之间的数量关系，并证明．
参考答案
1．【答案】B
2．【答案】A
3．【答案】B
4．【答案】A
5．【答案】D
6．【答案】B
7．【答案】B
8．【答案】D
9．【答案】C
10．【答案】A
11．【答案】25
12．【答案】k2＜k1＜k4＜k3
13．【答案】16
14．【答案】y=43x-73
15．【答案】40
16．【答案】5.1
17．【答案】（1）解：原式= (26)2-(35)2
= 24-45
=-21
（2）解：原式= 22+3-22+32
= 322+332
18．【答案】证明：∵四边形ABCD为平行四边形，
∴AD∥BC．
∴∠DAC=∠BCA．
∵O是平行四边形ABCD对角线的交点，
∴AO=CO．
在△AOF和△COE中 ∠DAC=∠BCAAO=CO∠AOF=∠EOC ，
∴△AOE≌△COF（ASA）．
∴EO=FO．
∴四边形AECF为平行四边形
19．【答案】解：如图所示：
20．【答案】（1）解：由题意可得：
一次函数y＝2x﹣b的交换函数是y＝﹣bx+2，
故答案为：y＝﹣bx+2；
（2）x＝1
（3）解：函数y＝2x﹣b与y轴的交点是（0，﹣b），函数y＝﹣bx+2与y轴的交点为（0，2），
由（2）知，当b≠﹣2时，（1）中两个函数图象交点的横坐标是x＝1，
∵（1）中两个函数图象与y轴围成的三角形的面积为4，
∴|-b-2|×12 ＝4，
解得b＝6或b＝﹣10，
即b的值是6或﹣10．
21．【答案】（1）证明： ∵ 四边形 ABCD 是平行四边形，
∴AD//BC .
∴∠DAE=∠AEB .
∵AE 平分 ∠BAD ，
∴∠DAE=∠BAE .
∴∠BAE=∠AEB .
∴AB=BE .
同理： AB=AF .
∴AF=BE .
∴ 四边形 ABEF 是平行四边形.
∵AB=BE ，
∴ 四边形 ABEF 是菱形；
（2）解：过 P 作 PH⊥AD 于 H ，交 BC 于 G ，如图所示：
则 GH⊥BC ，
∵ 四边形 ABEF 是菱形， ∠ABC=60° ， AB=6 ，
∴AB=AF=6 ， AE⊥BF ， BP=FP ， ∠ABF=∠AFB=30° ，
∴AP=12AB=3 ， FP=BP=3AP=33 ，
∴AH=12AP=32 ， PH=12PF=332 ，
∴DH=AD-AH=9-32=152 ，
∴PD=PH2+DH2=(332)2+(152)2=37 ，
同理： PG=PH=332 ， BG=3PG=92 ，
∵ 四边形 ABCD 是平行四边形，
∴CD=AB=6 ， BC=AD=9 ，
∴CG=BC-BG=92 ，
∴PC=PG2+CG2=(332)2+(92)2=33 ，
∵PC2+CD2=PD2 ，
∴△PCD 是直角三角形， ∠DCP=90° .
22．【答案】（1）15×(163+164+165+165+168)=165(cm) ，
∴甲队女演员身高的平均数是165cm，
把这些数从小到大排列，则中位数是165cm，
165cm出现了2次，出现的次数最多，则众数是165cm；
（2）乙队女演员身高的平均数 =15×(162+164+164+167+168)=165(cm) ，
甲队数据方差
s甲2=15×[(163-165)2+(164-165)2+(165-165)2+(165-165)2+(168-165)2]=2.8 ，
乙队数据方差
s乙2=15×[(162-165)2+(164-165)2+(164-165)2+(167-165)2+(168-165)2]=4.8 ，
∵s甲2∴甲队女演员的身高更整齐.
23．【答案】（1）2﹣k
（2）解：由（1）可得y=kx+2﹣k，
向下平移2个单位所得直线的解析式为y=kx﹣k，
令x=0，得y=﹣k，令y=0，得x=1，
∴A（1，0），B（0，﹣k），
∵C（1+k，0），
∴AC=|1+k﹣1|=|k|，
∴S△ABC= 12 AC•|yB|= 12 |k|•|﹣k|= 12 k2，
∴12 k2=2，解得k=±2；
（3）解：依题意，当自变量x在1≤x≤3变化时，函数值y的最小值大于0.
分两种情况：
ⅰ）当k＞0时，y随x增大而增大，
∴当x=1时，y有最小值，最小值为k+2﹣k=2＞0，
∴当 k＞0时，函数值总大于0；
ⅱ）当k＜0时，y随x增大而减小，
∴当x=3时，y有最小值，最小值为3k+2﹣k=2k+2，
由2k+2＞0得k＞﹣1，
∴﹣1＜k＜0.
综上，当k＞0或﹣1＜k＜0时，函数值y总大于0.
24．【答案】（1）证明： ∵D 点为 AC 的中点，
∴AD=CD ，
∵AF//BE ，
∴∠FAD=∠ECD ，
在 △ADF 和 △CDE 中，
∠FAD=∠ECD∠ADF=∠CDEAD=CD ，
∴△ADF≌△CDE(AAS) ，
∴AF=CE
（2）解： ∵AF//BE,AF=CE ，
∴四边形 AFCE 为平行四边形，
∵AF=CF=4 ，
∴四边形 AFCE 为菱形，
∴AD⊥EF,EF=2FD ，
∵∠AFD=30° ，
∴AD=12AF=2 ，
∴FD=AF2-AD2=42-22=23 ，
∴EF=2FD=43
25．【答案】（1）证明：作 NH⊥BC ，垂足为H，
∵四边形ABCD为正方形，
∴∠B=∠NAB=90°，∠NHB=90°，
∴∠B=∠NAB=∠NHB=90°，
∴四边形ABHN为矩形，
∴HN=AB=AD ，
∵MN⊥DE ，
∴∠EDA+∠DNP=90° ，又 ∠HNM+∠DNP=90° ，
∴∠EDA=∠HNM ，
∴△HNM≌△ADE ，
∴MN=DE ；
（2）解：①∠DGF=45° .
∵ 点F与点C关于直线 DE 对称，且四边形 ABCD 是正方形，
∴DC=DF=AD ， ∠CDG=∠FDG=(90-x)° ，
∴∠FDA=∠FDG-∠ADG=(90-2x)° ，
∴ 在等腰 △DAF 中， ∠DAF=12(180°-∠ADF)=(45+x)° ，
又 ∵∠DAF=∠ADG+∠DGF=x°+∠DGF ，
∴∠DGF=45° ；
②AF=2BG .
证明：连接 CG ， CF ，
由对称性可知 GC=GF ， ∠DGC=∠DGF=45°
即 △CGF 是等腰直角三角形，
∴FC =CG2+FG2=2CG2=2CG ，
∴CFCG=2 ，
∵四边形ABCD为正方形，
∴AC=CB2+AB2=2CB2=2CB ，
∵CACB=2 ，
∴CFCG=CACB ，
又 ∵∠ACF=∠BCG=45°-∠ACG ，
∴△CAF∽△CBG ，
∴AFBG=CACB=2 ，
∴AF=2BG ．t/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5