
人教B版 (2019)选择性必修 第一册第二章 平面解析几何2.7 抛物线及其方程2.7.1 抛物线的标准方程导学案及答案
展开抛物线的标准方程
【学习目标】
1.正确理解抛物线的概念
2.了解抛物线的标准方程推导过程,掌握抛物线标准方程的四种标准形式,并能求出基本的抛物线方。
【学习过程】
一、问题与例题
阅读教材页并完成以下问题:
1.平面内与一个定点F和一条定直线()_________的点的轨迹叫做抛物线,_______叫做抛物线的焦点,________叫做抛物线的准线。
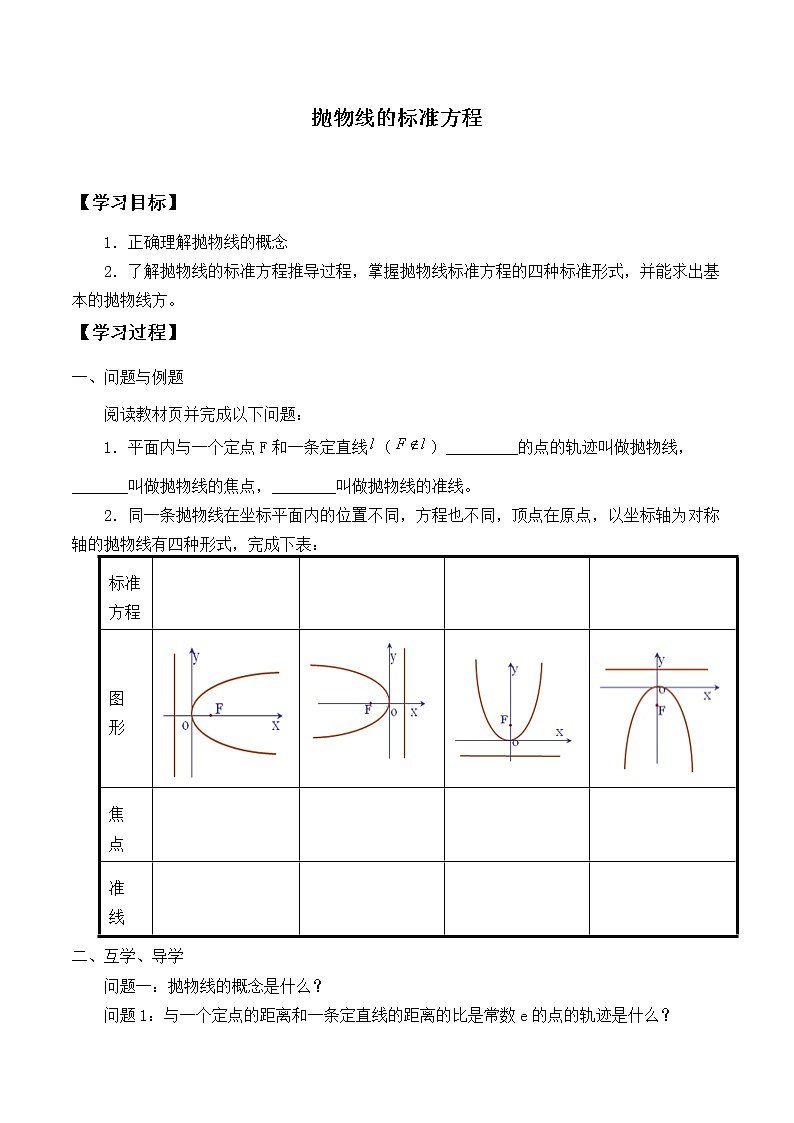
2.同一条抛物线在坐标平面内的位置不同,方程也不同,顶点在原点,以坐标轴为对称轴的抛物线有四种形式,完成下表:
标准 方程 |
|
|
|
|
图 形 | ||||
焦 点 |
|
|
|
|
准 线 |
|
|
|
|
二、互学、导学
问题一:抛物线的概念是什么?
问题1:与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹是什么?
答:
问题2:当时,动点的轨迹又是什么?
答:
问题3:在抛物线定义中,条件“l不经过点F”去掉是否可以?
答:
问题二:如何根据抛物线的概念来探究抛物线的标准方程?
问题1:求曲线方程的步骤是什么?
答:
问题2:比较椭圆、双曲线的标准方程的建立过程,你认为应如何选择坐标系,所求的抛物线的方程更简单?
推导方程:
问题3:观察图形及方程,的几何意义是什么?
答:
问题4:如果焦点不在轴正半轴上,而是在轴正、负半轴上或者负半轴上,那么抛物线的标准方程是什么?
答:
问题5:确定抛物线的标准方程时,一般需要确定几个量?
答:
问题:6:你能说明二次函数的图像为什么是抛物线?其焦点坐标、准线方程?
答:
例1:已知抛物线的标准方程是,求它的焦点坐标和准线方程。
三、方法技巧
求焦点坐标和准线方程的步骤:
变式训练1 :(1)(2014安徽高考)抛物线的准线方程是 ( )
A.y=-1 B.y=-2 C.x=-1 D.x=-2
(2)已知抛物线的焦点是,求它的标准方程。
四、目标检测(检学)
1.抛物线y2=4x的焦点坐标为 ;准线方程为 。
2.若抛物线的方程为x=2ay2(a>0),则焦点到准线的距离p= 。
3.焦点坐标为(0,2)的抛物线的标准方程为 。
4.以为焦点的抛物线的标准方程是_________。
5.若抛物线y2=8x上一点P到其焦点的距离为9,则点P的坐标为___。
五、配餐作业
A组
1.已知抛物线的准线方程为x=-7,则抛物线的标准方程为 ( )
A.=-28y B.=28x C.=-28x D.=28y
2.抛物线y=-的准线方程是 ( )
A.x= B.x=1 C.y=1 D.y=2
3.焦点是,则抛物线的标准方程为
4.焦点到准线的距离等于2,则抛物线的标准方程时 ,
5.抛物线方程为7x+4=0,则焦点坐标为 ( )
A. B. C. D.
B组
6.抛物线上一点到焦点的距离等于6,则该点的坐标
7.求下列抛物线的焦点坐标和准线方程:
(1) (2)
8.抛物线上一点到焦点的距离是,则点到准线的距离是 ,点的横坐标是
9.顶点在原点,对称轴是轴,并经过点,求抛物线的标准方程,并画出图形。
C组
10. 是抛物线上一点,是抛物线的焦点,以为始边、为终边的角,求。
六、复习上节内容
问题一:抛物线的概念是什么?
问题二:抛物线的标准方程?
问题1:抛物线的标准方程有几种形式?其焦点坐标及标准方程各是什么?
问题2:的几何意义是什么? 答:
问题3:四种抛物线的标准方程的相同点与不同点?
答:
七、备选题
1.已知P(8,a)在抛物线=4px上,且P到焦点的距离为10,则焦点到准线的距离为( )
A.2 B.4 C.8 D.16
2.以坐标轴为对称轴,以原点为顶点且过圆的圆心的抛物线的方程是A.
3.如图所示,方程x=ay2与y=ax+b2(ab≠0)的图象只能是( )
A B C D
4.已知抛物线的顶点在原点,对称轴为x轴,焦点在双曲线-=1上,则抛物线方程为( )
A.=8x B.=4x C.=2x D.=±8x
5.已知抛物线=2px(p>0)的准线与圆(x-3)2+=16相切,则p的值为( )
A. B.1 C.2 D.4
数学选择性必修 第一册2.7.1 抛物线的标准方程导学案: 这是一份数学选择性必修 第一册2.7.1 抛物线的标准方程导学案,共3页。学案主要包含了学习目标,学习重难点,学习过程,学习小结,精炼反馈等内容,欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第一册2.7.1 抛物线的标准方程导学案: 这是一份高中数学人教B版 (2019)选择性必修 第一册2.7.1 抛物线的标准方程导学案,共5页。学案主要包含了学习目标,学习过程,学习拓展,达标检测,课堂小结等内容,欢迎下载使用。
数学选择性必修 第一册2.7.1 抛物线的标准方程导学案: 这是一份数学选择性必修 第一册2.7.1 抛物线的标准方程导学案,共8页。学案主要包含了学习目标,学习过程,合作探究等内容,欢迎下载使用。













