2021-2022学年河南省驻马店第二初级中学七年级（下）期中数学试卷

2021-2022学年河南省驻马店第二初级中学七年级（下）期中数学试卷

1. 某种细菌的直径约为米，用科学记数法表示该细菌的直径约为米．

A.  B.  C.  D.

2. 下列计算正确的是

A.  B.  C.  D.

3. 若，，则

A. 5 B. 3 C. 15 D. 10

4. 长方形的面积是，一边长是3a，则它的另一边长是

A.  B.  C.  D.

5. 为了运用平方差公式计算，下列变形正确的是

A.  B.
C.  D.

6. 设，，则A、B的大小关系为

A.  B.  C.  D. 无法确定

7. 点P为直线l外一点，点A、B、C为直线上三点，，，，则点P到直线l的距离为

A. 2cm B. 3cm C. 小于3cm D. 不大于3cm

8. 如图，将一副三角尺按图中所示位置摆放，点F在AC上，其中，，，，，则的度数是
    

A.  B.  C.  D.

9. 观察：，，，据此规律，当时，代数式的值为

A. 1 B. 0 C. 1或 D. 0或

10. 把4张长为a、宽为的长方形纸片，按如图的方式拼成一个边长为的正方形，图中空白部分的面积为，阴影部分的面积为若，则a、b满足
    
    
     

A.  B.  C.  D.

11. 是完全平方式，则______.
12. 下表反映的是高速公路上匀速行驶的汽车在行驶过程中油箱的剩余油量升与时间时与之间的关系，该关系可以表示为______.

13. 如图，线段，垂足为点A，线段GD分别交AF、AE于点C，B，连结GF，则的度数为______.

14. 如图，某江水流向经过B，C，D三点拐弯后与原来相同，若，，则______.
    
     

15. 若与的两边分别平行，且比的2倍少，则______.
16. 计算：
    ；
    
    
    
    
    
    
    
     
17. 若，求的值．
    
    
    
    
    
    
     
18. 已知a、b、c为三角形的三边长，化简：
    
    
    
    
    
    
     
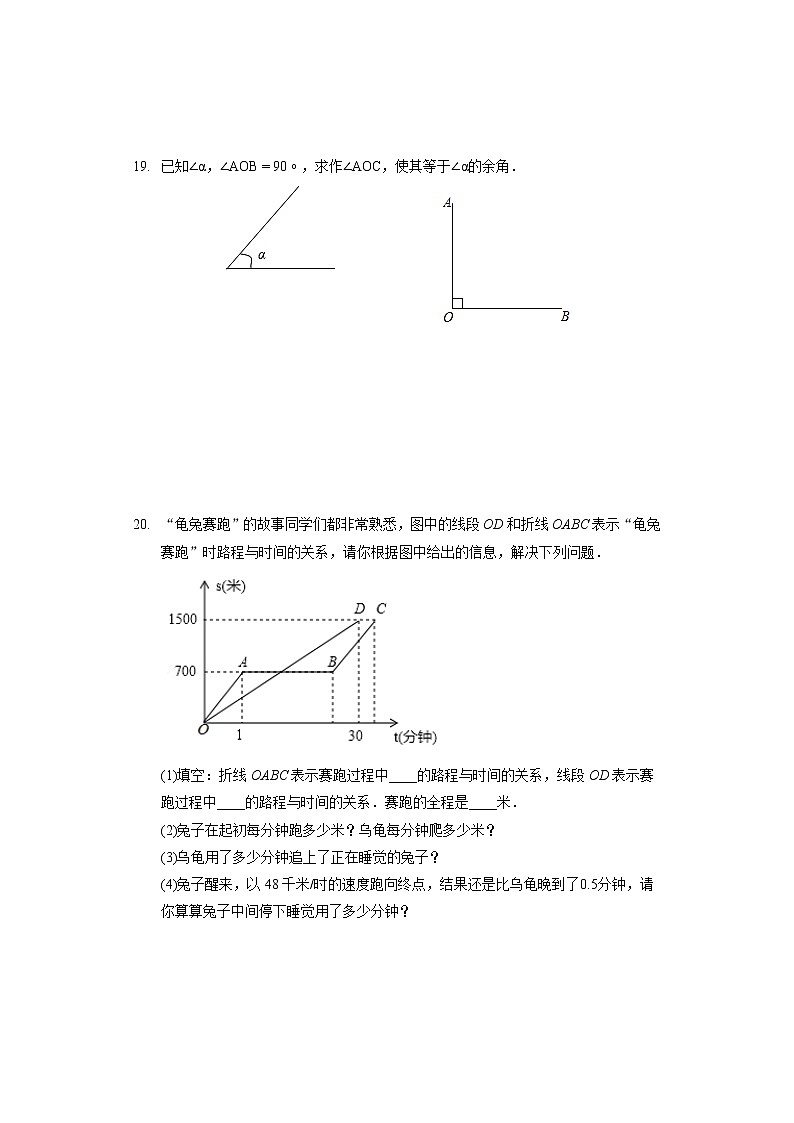
19. 已知，，求作，使其等于的余角．

20. “龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．

填空：折线OABC表示赛跑过程中____的路程与时间的关系，线段OD表示赛跑过程中____的路程与时间的关系．赛跑的全程是____米．

兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？

乌龟用了多少分钟追上了正在睡觉的兔子？

兔子醒来，以48千米/时的速度跑向终点，结果还是比乌龟晚到了分钟，请你算算兔子中间停下睡觉用了多少分钟？






 

21. 如图，已知：，垂足为点F，，垂足为点M，DM的延长线交AB于点B，且，点N在AD上，且，试说明
    
    
    
    
    
    
     
22. 从边长为a的正方形中减掉一个边长为b的正方形如图，然后将剩余部分拼成一个长方形如图
    
    上述操作能验证的等式是______；
    运用你从写出的等式，完成下列各题：
    ①已知，，，求的值；
    ②计算：
    
    
    
    
    
    
     

如图，已知，，点P是射线AM上一动点与点A不重合，BC，BD分别平分和，交射线AM于点C，推理时不需要写出每一步的理由
求的度数.
当点P运动时，那么与的大小关系是否发生变化？若不变，请找出它们的关系并说明理由；若变化，请找出变化规律.
当点P运动到使时，求的度数.







答案和解析

1.【答案】C
 

【解析】解：
故选：
绝对值小于1的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为，其中，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
 

2.【答案】C
 

【解析】

【分析】
此题主要考查了合并同类项以及幂的乘方运算、同底数幂的乘法运算，正确掌握相关运算法则是解题关键．
直接利用合并同类项法则以及幂的乘方运算法则、同底数幂的乘法运算法则分别化简得出答案．
【解答】
解：A、，无法计算，故此选项错误；
B、，故此选项错误；
C、，正确；
D、，故此选项错误．
故选  

3.【答案】A
 

【解析】解：，，，
，
故选
根据同底数幂的除法，由，，可得的值，本题得以解决．
本题考查同底数幂的乘法，解题的关键是明确同底数幂的乘法与除法之间的相互转化．
 

4.【答案】C
 

【解析】解：，
故选：
长方形的面积=长宽，由此列出式子
本题考查整式的除法；熟练掌握整式除法的运算法则是解题的关键．
 

5.【答案】B
 

【解析】解：运用平方差公式计算，
应变形为，
故选：
原式利用平方差公式的结构特征变形即可．
此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．
 

6.【答案】A
 

【解析】

【分析】
本题主要考查多项式乘以多项式的法则，注意不要漏项，漏字母，有同类项的合并同类项．根据多项式乘以多项式的法则，先把A、B进行整理，然后比较即可得出答案．
【解答】
解：，，
，
；
故选：  

7.【答案】D
 

【解析】解：连接直线外一点P与直线上任意点，所得线段中垂线段最短；
因为，，，
所以三条线段中，最短的是3cm，
所以点P到直线l的距离不大于
故选：
根据直线外一点到直线的垂线段的长度，叫做点到直线的距离，可得连接直线外一点P与直线上任意点，所得线段中垂线段最短；然后根据，，，可得三条线段的最短的是3cm，所以点P到直线l的距离不大于3cm，据此判断即可．
此题主要考查了点到直线的距离的含义以及特征，考查了分析推理能力的应用，解答此题的关键是要明确：连接直线外一点P与直线上任意点，所得线段中垂线段最短．
 

8.【答案】A
 

【解析】解：如图，

，，
，
，，
，
，
，
，
故选：
利用三角形的内角和定理可得，，由平行线的性质定理可得，利用三角形外角的性质可得结果．
本题主要考查了三角形的内角和定理，平行线的性质定理和外角的性质，求出，的度数是解本题的关键．
 

9.【答案】D
 

【解析】解：





当时，原式
当时，原式
故选：
先根据规律求x的值，再求代数式的值．
本题考查通过规律解决数学问题，发现规律，求出x的值是求解本题的关键．
 

10.【答案】D
 

【解析】

【分析】
本题考查了整式的混合运算，熟练运用完全平方公式是解题的关键.
先用a、b的代数式分别表示，，再根据，得，整理，得，所以
【解答】
解：，
，
，
，
整理，得，
，

故选  

11.【答案】
 

【解析】解：中间一项为加上或减去x和3的积的2倍，
故
这里首末两项是x和3这两个数的平方，那么中间一项为加上或减去x和3的积的2倍，故
本题是完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．
 

12.【答案】
 

【解析】解：由表格中数据的变化规律可知，行驶时间x每增加1小时，油箱内的余油量就减少10升，
所以油箱的剩余油量升与时间时与之间的关系式为，
故答案为：
根据表格中数据的变化规律进行计算即可．
本题考查函数关系式，理解表格中两个变量的对应数值的变化规律是得出正确答案的关键．
 

13.【答案】
 

【解析】解：，，
，
，，
，
，
，
，
故答案为：
根据三角形的内角和定理及对顶角的性质可求得，再利用三角形的内角和定理可得，进而可求解的度数．
本题主要考查三角形的内角和定理，掌握三角形的内角和定理是解题的关键．
 

14.【答案】
 

【解析】解：过点C作，

某江水流向经过B，C，D三点拐弯后与原来相同，
，
，
，
，
，
，

故答案为：
由某江水流向经过B，C，D三点拐弯后与原来相同，得，过点C作，则，由平行线的性质可得，，所以能求出，继而求出，根据平行线的性质即可求解．
此题考查平行线的性质，关键是过C点先作AB的平行线，由平行线的性质求解．
 

15.【答案】或
 

【解析】解：的两边分别与的两边平行，
或，
比的2倍少，
，
或
故答案为：或
由的两边分别与的两边平行，可得与相等或互补，又由比的2倍少，即可求得答案．
此题考查了平行线的性质．注意掌握得到与相等或互补是解此题的关键．
 

16.【答案】解：原式

；
原式


 

【解析】利用有理数的乘方的运算法则、负整数指数幂的性质、零指数幂的性质分别化简求出答案；
利用完全平方公式计算得出答案．
此题主要考查了有理数的乘方的运算法则、负整数指数幂的性质、零指数幂的性质、完全平方公式等知识，能够正确化简各数是解题关键．
 

17.【答案】解：

，
，
，
当时，原式



 

【解析】先去括号，再合并同类项，然后把代入化简后的式子进行计算即可解答．
本题考查了整式的混合运算-化简求值，准确熟练地进行计算是解题的关键．
 

18.【答案】解：，b，c是的三边的长，
，，，
，，，




 

【解析】首先根据三角形的三边关系确定，，，然后去绝对值，化简即可求得．
此题考查了三角形三边关系与绝对值的性质．解此题的关键是要注意符号．
 

19.【答案】解：如图所示：就是所求的角．

 

【解析】以OB为一边作，则就是所求．
本题考查了基本作图，作一个角等于已知角，以及余角的定义，是一个基础题．
 

20.【答案】解：
兔子，乌龟，1500 ；
结合图象得出：兔子在起初每分钟跑700米．
米，
乌龟每分钟爬50米．
分钟，
乌龟用了14分钟追上了正在睡觉的兔子．
千米米，
米/分，
分钟，
分钟，
兔子中间停下睡觉用了分钟．
 

【解析】

【分析】
此题要数形结合，根据兔子与乌龟的奔跑路程和时间的图象来求解．
【解答】
解：乌龟是一直跑的而兔子中间有休息的时刻；
折线OABC表示赛跑过程中兔子的路程与时间的关系；
线段OD表示赛跑过程中乌龟的路程与时间的关系；
由图象可知：赛跑的路程为1500米；
故答案为：兔子、乌龟、1500；
见答案；
见答案；
见答案.
本题主要考查动点，结合图形进行求解．  

21.【答案】证明：，，
垂直定义，
同位角相等，两直线平行，
两直线平行，同位角相等，
已知，
等量代换，
内错角相等，两直线平行，
两直线平行，同位角相等，
已知，
等量代换，
内错角相等，两直线平行
 

【解析】首先证明可得，进而可得，可证明，再根据平行线的性质可得，结合已知条件再证明
此题主要考查了平行线的判定和性质，关键是掌握内错角相等，两直线平行．两直线平行，内错角相等．
 

22.【答案】解：；
①，

解得
 ②原式…



 

【解析】解：第一个图形中阴影部分的面积是，第二个图形的面积是；

见答案.
分别求出两个图形中阴影部分的面积，建立等式即可；
①由上题得，代入求值即可；
②分别把括号内的多项式按照题的结论变形，再探究规律并化简求值．
本题考查平方差公式的几何背景及应用，难度适中，熟练掌握平方差公式是解决此题的关键；同时，还要注意探究算式的规律性这种题型在近几年的考试中多有涉及，需多加练习．
 

23.【答案】解：，
，
，
，
平分，BD平分，
，，
，
；
不变，：：
，
，，
平分，
，
：：1；
，
，
当时，则有，
，
，
由可知，，
，

 

【解析】由平行线的性质可求得，再根据角平分线的定义和整体思想可求得；
由平行线的性质可得，，再由角平分线的定义可求得结论；
由平行线的性质可得到，结合条件可得到，且，可求得的度数．
本题主要考查平行线的判定和性质，掌握平行线的判定和性质及整体思想的应用是解题的关键．