山西省吕梁市交城县2021-2022学年七年级下学期期中质量检测数学试题（含答案）

这是一份山西省吕梁市交城县2021-2022学年七年级下学期期中质量检测数学试题（含答案），共12页。试卷主要包含了体积为5的正方体棱长为，下列计算正确的是，下列说法错误的是，已知点A，线段AB的长度为，用“•”表示一种新运算等内容，欢迎下载使用。

选择题:（本大题共10个小题，每题3分，共30分）
1.体积为5的正方体棱长为
A. B. C. D.
2.下列计算正确的是
A. B. C. D.
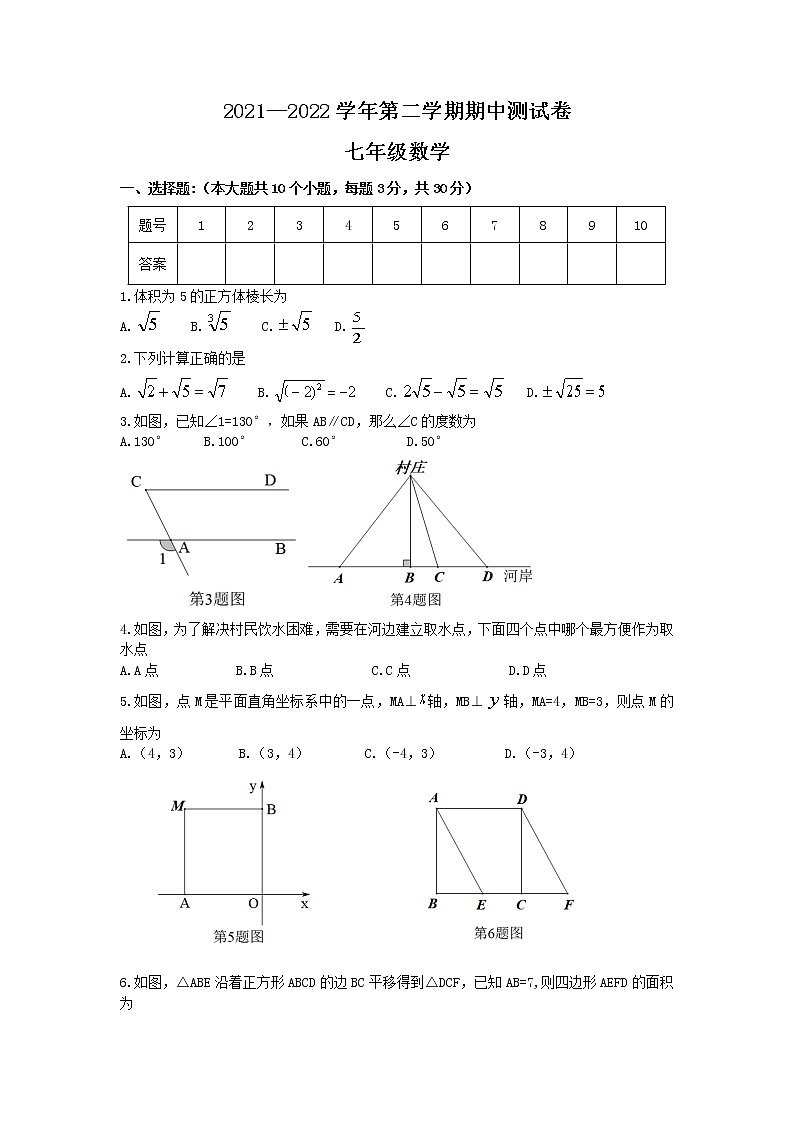
3.如图，已知∠1=130°，如果AB∥CD，那么∠C的度数为
A.130° B.100° C.60° D.50°
4.如图，为了解决村民饮水困难，需要在河边建立取水点，下面四个点中哪个最方便作为取水点
A.A点 B.B点 C.C点 D.D点
5.如图，点M是平面直角坐标系中的一点，MA⊥轴，MB⊥轴，MA=4，MB=3，则点M的坐标为
A.（4，3） B.（3，4） C.（-4，3） D.（-3，4）
6.如图，△ABE沿着正方形ABCD的边BC平移得到△DCF，已知AB=7,则四边形AEFD的面积为
38 B.42 C.49 D.
7.下列说法错误的是
A.同一平面内，两条不重合的直线的位置关系只有相交和平行
B.同旁内角互补，两直线平行
C.过一点有且只有一条直线与已知直线垂直
D.有部分无理数不能用数轴上的点表示
8.已知点A（3，5），B（-2，5），线段AB的长度为
A.3个单位长度 B.1个单位长度
C.5个单位长度 D.10个单位长度
9.如图，要添加一个条件使AB∥CD，则下列选项中正确的是
A.∠A=∠DCE B.∠B=∠DCE
C.∠A=∠B D.∠BCE=∠A+∠B
10.用“•”表示一种新运算：对于任意正实数•，例如10•21=，那么的运算结果为
A.13 B. 7 C.4 D.5
二、填空题：(本大题共5小题，每小题3分，共15分)
11.如图，直线AB，CD相交于点O，并且∠AOD=3∠AOC,则∠AOD的度数为 .
12.已知直线AB∥CD，把一个直角三角板按如图方式摆放，点E在直线AB上，点G在直线CD上，∠EGF=90°,∠DGF=136°,则∠BEG的度数为 .
13.在，0，-，1.1212121，，，0.818118111811118…中无理数的个数是 .
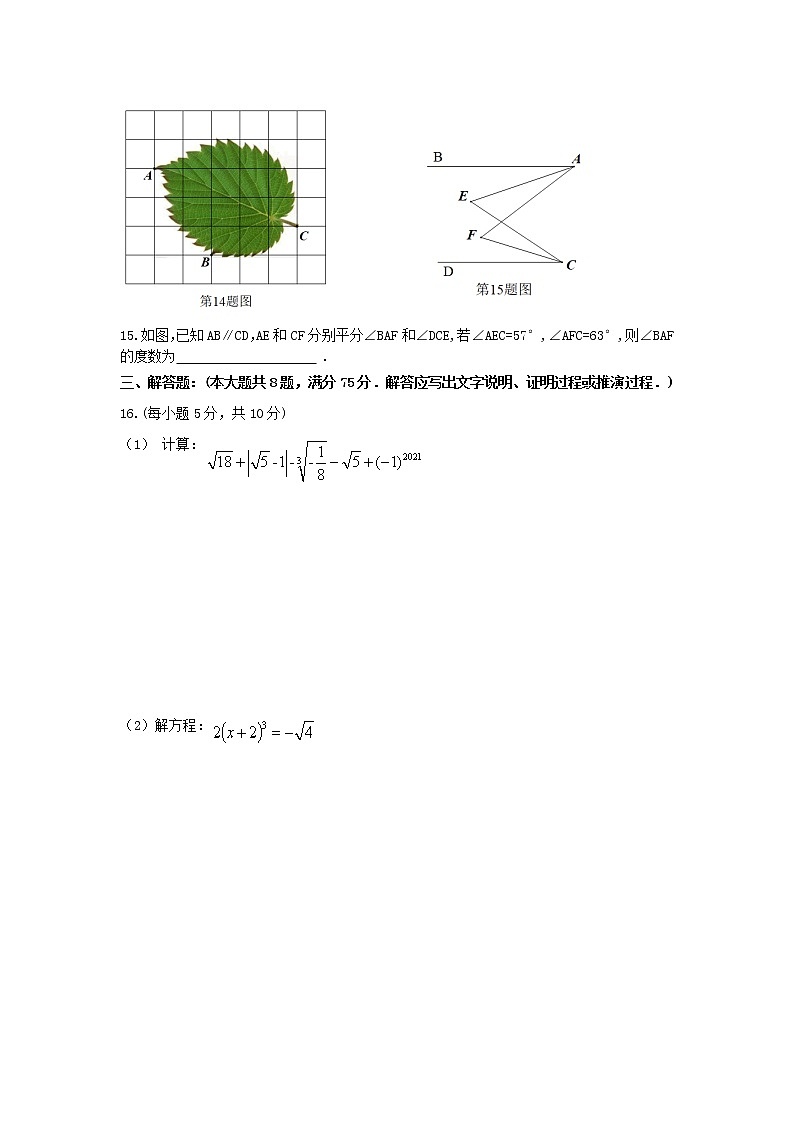
如图，是一片树叶标本，将其放在平面直角坐标系中，表示叶片尖端A，B两点的坐标分别为（-3，3）（-1，0），则叶柄底部点C的坐标为 .
15.如图，已知AB∥CD，AE和CF分别平分∠BAF和∠DCE,若∠AEC=57°,∠AFC=63°,则∠BAF的度数为 .
三、解答题：(本大题共8题，满分75分．解答应写出文字说明、证明过程或推演过程．)
16.(每小题5分，共10分)
（1） 计算：


（2）解方程：
17.（8分）（1）已知是的平方根，3是的算术平方根，求的平方根；
（2）已知正数的平方根是和，若，求的值.
18.（8分）已知点A是平面直角坐标系中的点.
若点A在第四象限的角平分线上，求得值；
若点A在第三象限，且到两坐标轴的距离和为9，请确定点A的坐标.
19.（10分）如图，在平面直角坐标系中，三角形ABC的顶点都在网格格点上，其中B点坐标为（6，4）
请写出点A，点C的坐标；
将△ABC先向左平移1个单位长度，再向上平移3个单位长度，得到△A′B′C′.请画出平移后的三角形，并写出△A′B′C′的三个顶点的坐标；
求△ABC的面积.
20.(7分)在数学课上老师提出了如下问题：
如图，∠B=160°，当∠A与∠D满足什么关系时，BC∥DE？
小明解答这个问题的思路和步骤如下，请你在横线上把未写出的步骤补充完整，或者填写依据.
解：满足的关系为：当∠D-∠A=20°时，BC∥DE.
过点A作AM∥BC
∴∠B+∠BAM=180°,( )
∵∠B=160°
∴∠BAM= °,
∴∠DAM=∠DAB+∠BAM=∠DAB+20°
∵∠D-∠A=20°( )
∴∠D=∠A+20°
∴∠D=∠DAM，（ ）
∴ ，（ ）
∴BC∥DE.（ ）
21.（8分）如图，已知DC∥AB，∠1=∠2，∠CGF=150°,∠AHF=70°,FN平分∠HFG.
求证：AB∥EF；
求∠EFN的度数.
22.（12分）先阅读下面的一段文字，再解答问题.
已知：在平面直角坐标系中，任意两点M()，N（），其两点之间的距离公式为.
同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点之间的距离公式可以简化为或.
已知点A（1，5），B（-3，6），试求A，B两点之间的距离；
已知点A，B在垂直于轴的直线上，点A的坐标为（-5，），AB=8，试确定点B的坐标；
已知点A（0，6），B（-3，2），C（3，2），请判断△ABC的形状，并说明理由.
23.（12分）问题情境：如图1，AB∥CD，∠BAM=45°,∠DCM=37°,求∠AMC的度数.
请你用两种不同的方法解答这个问题；
问题迁移：如图2，AB∥CD，点M在直线BD上运动，∠BAM=∠α,∠DCM=∠β.
①当点M在线段BD上运动时（不与点B,D重合），∠AMC、∠α、∠β之间有何数量关系？请说明理由.
②如果点M在线段BD之外运动时，请你直接写出∠AMC、∠α、∠β之间的数量关系.
2021—2022学年第二学期期中测试卷
七年级数学答案
一、选择题：（本题共10个小题，每题3分，共30分）
1—5 B C D B D 6—10 C D C A C
二、填空题：（本题共5个小题，每题3分，共15分）
11. 135° 12.46° 13. 3 14. （2，1） 15. 46°
三、简答题：
16.（本题共两个小题，每题5分，共10分）
解：（1）原式=
=……………4分
=……………5分
（2）
……………1分
……………2分
……………4分
……………5分
17.（第一问4分，第二问4分，共8分）
解：（1） ∵是的平方根，
∴
解之，得a＝2……………1分
∵3是3a+2b-3的算术立方根
∴3a+2b-3＝9
解之，得b=3……………2分
当a=2，b=3时
∴a+2b=8……………3分
∴a+2b的平方根为……………4分
（2）∵正数的平方根是和
∴……………5分
则方程可化为
……………6分
解得：……………7分
∵为正数
∴……………8分
18.解：（第一问4分，第二问4分，共8分）
（1）∵点A在第四象限的角平分线上
2a+3a-1=0 ……………2分
∴a= ……………4分
（2）∵点A在第三象限，且到两坐标轴的距离和为9
∴-2a-3a+1=9……………6分
∴a= ……………7分
∴A()……………8分
19.（第一问2分，第二问5分，第三问3分，共10分）
（1）A(3,-1),C(2,3)……………2分
（2）如图△ABC与△A′B′C'即为所求；……………4分
A′（2，2），B′（5，7），C′（1，6）……………7分
（3）……………10分
20.（每空1分，共7分）
两直线平行，同旁内角互补 20 已知 等量代换
AM∥DE 内错角相等，两直线平行
如果两条直线都与第三条直线平行，那么这两条直线也互相平行
21.（第一问2分，第二问6分，共8分）
（1）证明：∵∠1=∠2
∴DC∥EF……………1分
∵DC∥AB
∴AB∥EF……………2分
(2)解：∵DC∥EF
∴∠CGF+∠GFE=180°……………3分
∵∠CGF=150°
∴∠GFE=30° ……………4分
∵∠AFH=70°,EF∥AB
∴∠EFH=∠AHF=70° ……………5分
∵∠HFG=∠GFE+∠EFH
∴∠HFG=30°+70°=100°……………6分
∵FN平分∠HFG
∴∠HFN=∠HFG=50° ……………7分
∴∠EFN=∠EFH-∠HFN=20° ……………8分
22.（第一问2分，第二问5分，第三问5分，共12分）
解：（1）∵A(1,5),B(-3,6)
∴AB= =……………2分
（2）∵A，B在垂直于轴的直线上，
∴点A与点B的纵坐标相等……………3分
设B（,-12）……………4分
∴……………5分
∴……………6分
∴B(3,-12)或（-13，-12）……………7分
△ABC的形状为等腰三角形……………8分
∵A（0，6），B（-3，2），C（3，2）
∴AB= =5……………9分
AC= =5……………10分
BC= =6……………11分
∴AB=AC=5
∴△ABC的形状为等腰三角形……………12分
23.（第一问6分，第二问4分，第三问2分，共12分）
解：（1）方法一：过点M作MN∥AB
∴∠AMN=∠BAM=45°……………1分
∵AB∥CD
∴MN∥CD
∴∠CMN=∠DCM=37° ……………2分
∴∠AMC=∠AMN+∠CMN=45°+37°=82° ……………3分
方法二：延长AM交CD于点E
∵AB∥CD
∴∠CEM=∠BAM=45° ……………4分
∵∠DCM=37°
∴∠CME=180°-∠DCM-∠CEM=98° ……………5分
∴∠AMC=180°-∠CME=82° ……………6分
（2）①∠AMC=∠α+∠β……………7分
过点M作MN∥AB
∴∠AMN=∠BAM=∠α……………8分
∵AB∥CD
∴MN∥CD
∴∠CMN=∠DCM=∠β ……………9分
∴∠AMC=∠AMN+∠CMN=∠α+∠β ……………10分
②当点M在点B的上方时：∠AMC=∠β-∠α……………11分
当点M在点B的下方时：∠AMC=∠α-∠β……………12分
题号
1
2
3
4
5
6
7
8
9
10
答案