2022中考数学解答题专题29 三角函数的应用（Word，基础 培优，教师版 学生版））

专题29 三角函数的应用（提优）

1．如图，燕尾槽的横断面是等腰梯形ABCD，现将一根木棒MN放置在该燕尾槽中，木棒与横断面在同一平面内，厚度等不计，它的底端N与点C重合，且经过点A．已知燕尾角∠B＝54.5°，外口宽AD＝180毫米，木棒与外口的夹角∠MAE＝26.5°，求燕尾槽的里口宽BC（精确到1毫米）．（参考数据：sin54.5°≈0.81，cos54.5°≈0.58，tan54.5°≈1.40，sin26.5°≈0.45，cos26.5°≈0.89，tan26.5°≈0.50）

2．如图，吊车在水平地面上吊起货物时，吊绳BC与地面保持垂直，吊臂AB与水平线的夹角为64°，吊臂底部A距地面1.5m．

（1）当吊臂底部A与货物的水平距离AC为5m时，求吊臂AB的长；

（2）如果该吊车吊臂的最大长度AD为20m，那么从地面上吊起货物的最大高度是多少？（吊钩的长度与货物的高度忽略不计，计算结果精确到0.1m，参考数据：sin64°≈0.90，cos64°≈0.44，tan64°≈2.05）

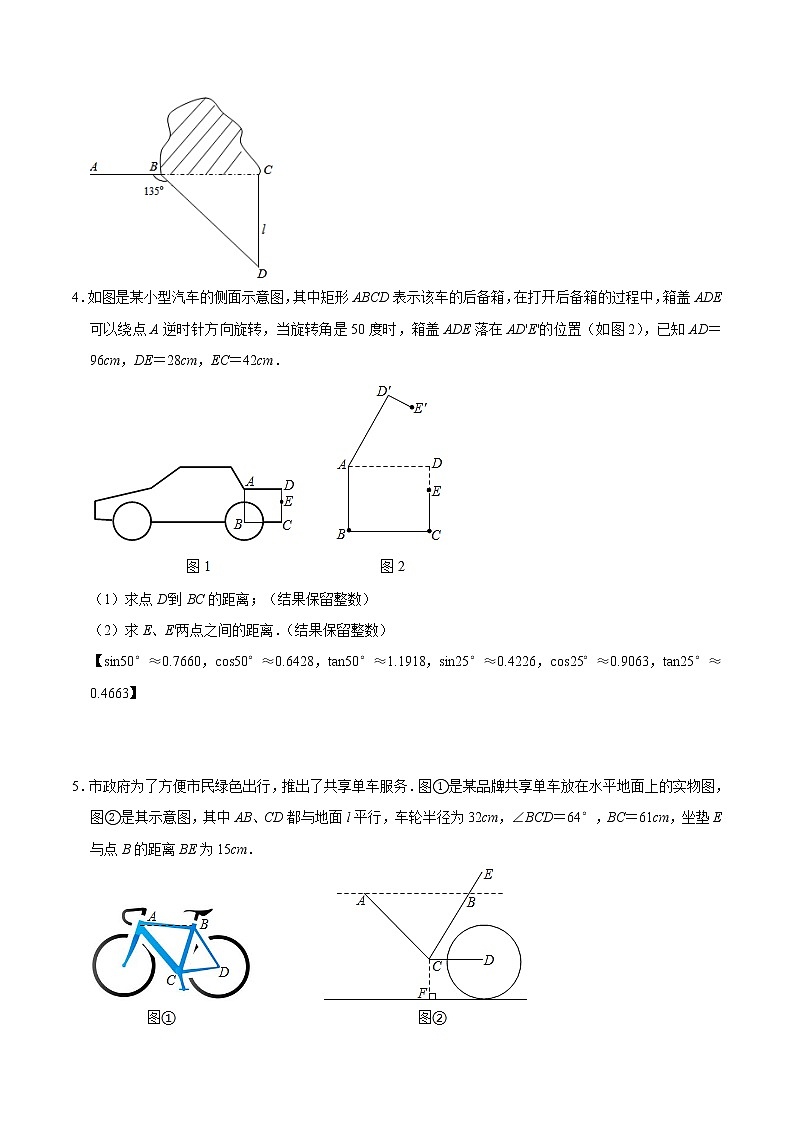
3．如图，修公路遇到一座山，于是要修一条隧道，为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过点C作直线AB的垂线l，过点B作一直线（在山的旁边经过），与l相交于D点，经测量∠ABD＝135°，BD＝800m，求直线l上距离D点多远的C处开挖？（1.414，精确到1米）

4．如图是某小型汽车的侧面示意图，其中矩形ABCD表示该车的后备箱，在打开后备箱的过程中，箱盖ADE可以绕点A逆时针方向旋转，当旋转角是50度时，箱盖ADE落在AD'E'的位置（如图2），已知AD＝96cm，DE＝28cm，EC＝42cm．

（1）求点D'到BC的距离；（结果保留整数）

（2）求E、E'两点之间的距离．（结果保留整数）

【sin50°≈0.7660，cos50°≈0.6428，tan50°≈1.1918，sin25°≈0.4226，cos25°≈0.9063，tan25°≈0.4663】

5．市政府为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面上的实物图，图②是其示意图，其中AB、CD都与地面l平行，车轮半径为32cm，∠BCD＝64°，BC＝61cm，坐垫E与点B的距离BE为15cm．

（1）求坐垫E到地面的距离；

（2）根据经验，当坐垫E到CD的距离调整为人体腿长的0.8时，坐骑比较舒适．小明的腿长约为80cm，现将坐垫E调整至坐骑舒适高度位置E'，求EE'的长．

（结果精确到0.1cm，参考数据：sin64°≈0.90，cos64°≈0.44，tan64°≈2.05）

6．随州市新厥水一桥（如图1），斜拉桥又称斜张桥，主要由索塔、主梁、斜拉索组成，某座斜拉桥的部分截面图如图2所示，索塔AB和斜拉索（图中只画出最短的斜拉索DE和最长的斜拉索AC）均在同一平面内，BC在水平桥面上，已知∠ABC＝∠DEB＝45°，∠ACB＝30°，BE＝6米，AB＝5BD．

（1）求最短的斜拉索DE的长．

（2）求最长的斜拉索AC的长．

7．如图1，通海桥是西宁市海湖新区地标建筑，也是我省首座大规模斜拉式大桥，通海桥主塔两侧斜拉链条在夜间亮灯后犹如天鹅之翼，优雅非凡．某数学“综合与实践”小组的同学利用课余时间按照如图2所示的测量示意图对该桥进行了实地测量，测得如下数据：∠A＝30°，∠B＝45°，斜拉主跨度AB＝260米．

（1）过点C作CD⊥AB，垂足为D，求CD的长（取1.7）；

（2）若主塔斜拉链条上的LED节能灯带每米造价800元，求斜拉链条AC上灯带的总造价是多少元？

8．今年第16号台风“浪卡”已经于10月13日在海南琼海市登录．台风来袭时，某绿化带一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上，树的顶部恰好接触到地面D处，测得∠ACD＝60°，∠ADC＝37°，AD＝5米，求这棵大树AB的高．（结果精确到0.1米）（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，1.73）

9．如图，四边形钢板是某机器的零部件，工程人员在设计时虑到飞行的稳定性和其他保密性原则，使得边沿AD的长度是边沿BC长度的三倍，且它们所在的直线互相平行，检测员王刚参与了前期零件的基础设计，知道∠ABC＝45°，边沿CD所在直线与边沿BC所在直线相交后所成的锐角为30°（即P在BC的延长线上，∠DCP＝30°），经测量BC的长度为7米，求零件的边沿CD的长．（结果保留根号）

10．《中华人民共和国道路交通管理条例》规定：“小汽车在城市街道上的行驶速度不得超过70千米/时．”如图所示，已知测速站M到公路l的距离MN为60米，一辆汽车在公路l上由东向西匀速行驶，测得此车从点A行驶到点B所用的时间为4秒，并测得∠AMN＝60°，∠BMN＝30°，计算此车从A到B每秒行驶多少米（结果精确到个位），并判断此车是否超过限速．（参考数据：1.732，1.414）

11．图1是一台实物投影仪，图2是它的示意图，折线B﹣A﹣O表示固定支架，AO垂直水平桌面OE于点O，点B为旋转点，BC可转动，当BC绕点B顺时针旋转时，投影探头CD始终垂直于水平桌面OE，经测量：AO＝6.4cm，CD＝8cm，AB＝40cm，BC＝45cm，

（1）如图2，∠ABC＝70°，BC∥OE．

①填空：∠BAO＝　   　°；

②投影探头的端点D到桌面OE的距离　   　．

（2）如图3，将（1）中的BC向下旋转，∠ABC＝30°时，求投影探头的端点D到桌面OE的距离．（参考数据：sin70°≈0.94，cos70°≈0.34，sin40°≈0.64，cos40°≈0.77）

12．智能手机如果安装了一款测量软件“SmartMeasure”后，就可以测量物高、宽度和面积等．如图，打开软件后将手机摄像头的屏幕准星对准脚部按键，再对准头部按键，即可测量出人体的高度．其数学原理如图②所示，测量者AB与被测量者CD都垂直于地面BC．

（1）若手机显示AC＝2m，AD＝2.5m，∠CAD＝53°，求此时CD的高．（结果保留根号）（sin53°，cos53°，tan53°）

（2）对于一般情况，试探索手机设定的测量高度的公式：设AC＝a，AD＝b，∠CAD＝α，即用a、b、α来表示CD．（提示：sin2α+cos2α＝1）

13．如图，根据道路管理规定，直线l的路段上行驶的车辆，限速60千米/时，已知测速站点M距离直线l的距离MN为30米（如图所示），现有一辆汽车匀速行驶，测得此车从A点行驶到B点所用时间为6秒，∠AMN＝60°，∠BMN＝45°．

（1）计算AB的长；

（2）通过计算判断此车是否超速．（1.4，1.7）

14．如图，河流的两岸PQ、MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD＝50米，某人在河岸MN的A处测的∠DAN＝35°，然后沿河岸走了130米到达B处，测的∠CBN＝60°，求河流的宽度CE（结果保留整数）．

（参考数据：sin35°≈0.6，cos35°≈0.8，tan35°≈0.7，1.7）

15．文物探测队探测出某建筑物下面有地下文物，为了准确测出文物所在的深度，他们在文物上方建筑物的一侧地面上相距20米的A、B两处，用仪器测文物C，探测线与地面的夹角分别是30°和60°，求该文物所在位置的深度（精确到0.1米）．

16．超速行驶是引发交通事故的主要原因．上周末，小明和三位同学尝试用自己所学的知识检测车速，如图，观测点设在到永丰路的距离为100米的点P处．这时，一辆小轿车由西向东匀速行驶，测得此车从A处行驶到B处所用的时间为4秒，∠APO＝60°，∠BPO＝45°．

（1）求A、B之间的路程；

（2）请判断此车是否超过了永丰路每小时54千米的限制速度？（参考数据：1.73）

17．在一次综合实践课上，同学们为教室窗户设计一个遮阳篷，小明同学绘制的设计图如图所示，其中AB表示窗户，且AB＝2米，BCD表示直角遮阳蓬，已知当地一年中正午时刻太阳光与水平线CD的最小夹角∠PDN＝18.6°，最大夹角∠MDN＝64.5°

请你根据以上数据，帮助小明同学计算出遮阳篷中CD的长是多少米？（结果精确到0.1）

（参考数据：sin18.6°≈0.32，tan18.6°≈0.34，sin64.5°≈0.90，tan64.5°≈2.1）

18．如图是小强洗漱时的侧面示意图，洗漱台（矩形ABCD）靠墙摆放，高AD＝80cm，宽AB＝48cm，小强身高166cm，下半身FG＝100cm，洗漱时下半身与地面成80°（∠FGK＝80°），身体前倾成125°（∠EFG＝125°），脚与洗漱台距离GC＝15cm（点D，C，G，K在同一直线上）．

（1）此时小强头部E点与地面DK相距多少厘米？

（2）此时小强头部E点是否恰好在洗漱盆AB的中点O的正上方？若是，请说明理由；若不是，他应向前还是向后移动多少厘米，使头部E点恰好是在洗漱盆AB的中点O的正上方？（sin80°≈0.98，cos80°≈0.17，1.41，结果精确到1cm）

19．某款篮球架的示意图如图所示，已知底座BC＝0.60米，底座BC与支架AC所成的角∠ACB＝75°，支架AF的长为2米，篮板顶端F点到篮筐点D的距离FD＝1.35米，篮板底部支架HE与支架AF所成的角∠FHE＝60°，求篮筐D到地面的距离（精确到0.1米）．（参考数据：cos75°≈0.26，sin75°≈0.97，tan75°≈3.73，1.73，1.41）

20．某中学广场上的旗杆AB，在某一时刻它的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为3米，落在斜坡上的影长CD为2米，AB⊥BC，同一时刻，光线与水平面的夹角为60°，1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆的高度（若结果中有根号，请保留根号）