2022年中考数学解答题专题17——二次函数综合（Word版，基础 培优，教师版 学生版，共4份））

专题17 二次函数综合（提优）

1．如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．

（1）求此抛物线；

（2）求直线AB的解析式；

（3）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，直接写出点M的坐标；若不存在，请说明理由．

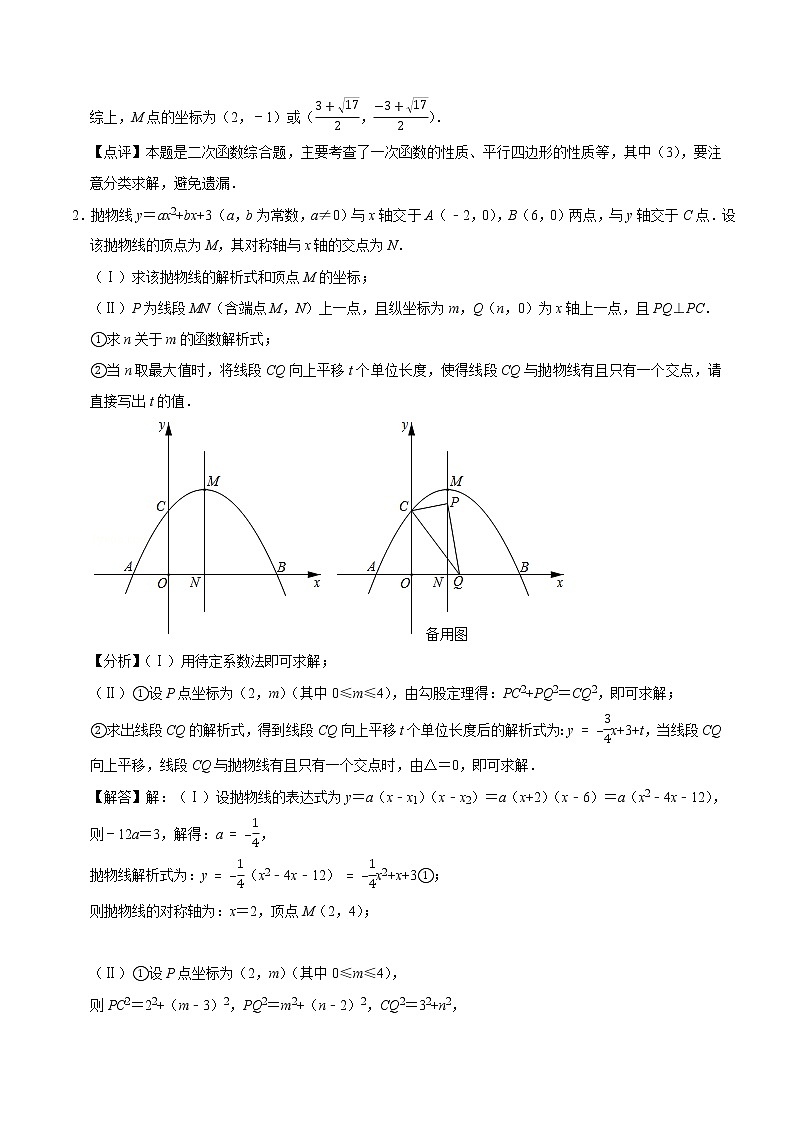
2．抛物线y＝ax2+bx+3（a，b为常数，a≠0）与x轴交于A（﹣2，0），B（6，0）两点，与y轴交于C点．设该抛物线的顶点为M，其对称轴与x轴的交点为N．

（Ⅰ）求该抛物线的解析式和顶点M的坐标；

（Ⅱ）P为线段MN（含端点M，N）上一点，且纵坐标为m，Q（n，0）为x轴上一点，且PQ⊥PC．

①求n关于m的函数解析式；

②当n取最大值时，将线段CQ向上平移t个单位长度，使得线段CQ与抛物线有且只有一个交点，请直接写出t的值．

3．如图，抛物线y＝﹣x2+2x+3与x轴正半轴，y轴正半轴分别交于点A、B，点G为抛物线的顶点．

（1）求顶点G的坐标；

（2）求抛物线与x轴的交点坐标；

（3）若点P是抛物线上一点，点P的横坐标为m，当x≥m，此函数图象上的函数值y随x的增大而减小，写出m的取值范围；

（4）点M、N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为3个单位和5个单位长度，点Q为抛物线上点M、N之间（含M、N）的一个动点，求点Q的纵坐标yQ的取值范围．

4．已知，如图，抛物线y＝ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．

（1）求直线AB的解析式；

（2）求抛物线的解析式；

（3）当点P运动到什么位置时，△PAB的面积有最大值？

5．在平面直角坐标系xOy中，抛物线y＝mx2﹣2mx+m﹣3与x轴交于点A、B．

（1）①求m的取值范围；

②当抛物线经过原点时，求抛物线的解析式；

③求抛物线的顶点坐标；

（2）若线段AB上有且只有5个点的横坐标为整数，求m的取值范围；

（3）若抛物线在﹣3＜x＜0这一段位于x轴下方，在5＜x＜6这一段位于x轴上方，求m的值．

6．如图，在平面直角坐标系中，抛物线yx2﹣2x经过坐标原点，与x轴正半轴交于点A，该抛物线的顶点为M，直线yx+b经过点A，与y轴交于点B，连接OM．

（1）求b的值及点M坐标．

（2）将直线AB向下平移，得到过点M的直线y＝mx+n，且与x轴负半轴交于点C，取点D（2，0），连接DM，此时发现∠ADM﹣ACM是个常数，请写出这个常数，并证明．

（3）点E是线段AB上一动点，点F是线段OA上一动点，连接EF，线段EF的延长线与线段OM交于点G，当∠BEF＝2∠BAO时，是否存在点E，使得3GF＝4EF？若存在，直接写出点E的坐标；若不存在，请说明理由．

7．如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+2x+3与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，抛物线顶点为点D．

（1）求B，C，D三点坐标；

（2）如图1，抛物线上有E，F两点，且EF∥x轴，当△DEF是等腰直角三角形时，求线段EF的长度；

（3）如图2，连接BC，在直线BC上方的抛物线上有一动点P，当△PBC面积最大时，点P坐标．

8．如图，已知二次函数y＝ax2+bx+4的图象与x轴交于A、B，与y轴交于点C，∠ACB＝90°，且OC＝2OA．

（1）求此二次函数的关系式；

（2）若点P为直线BC上方抛物线上的一动点，PM⊥BC于M，PN∥y轴交BC于N，求△PMN周长的最大值及此时是P的坐标；

（3）过点A作BC的平行线交抛物线于D，E为直线AD上一动点，F为平面内一动点，当以B、C、E、F为顶点的四边形为菱形时，请直接写出点E坐标．

9．如图，在平面直角坐标系中，直线y＝kx+1与x轴交于点A，与y轴交于点C，过点C的抛物线y＝ax2﹣（6a﹣2）x+b与直线AC交于另一点B（4，3）．

（1）求抛物线的表达式；

（2）已知x轴上一动点Q（m，0），连接BQ，若△ABQ与△AOC相似，求出m的值．

10．如图，抛物线y＝ax2+bx+6经过A（﹣2，0）、B（4，0）两点，与y轴交于点C，点D是抛物线上一动点，设点D的横坐标为m（1＜m＜4），连结AC、BC、DB、DC．

（1）求抛物线的函数表达式．

（2）当△BCD的面积等于△AOC的面积的时，求m的值．

（3）当m＝2时，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B、D、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的的坐标；若不存在，请说明理由．

11．如图1，抛物线y＝﹣x2+bx+c与x轴相交于点A（﹣1，0）和点B，交y轴于点C，CO＝3AO，点P是抛物线上第一象限内的一动点，点Q在抛物线上．

（1）求抛物线的解析式；

（2）过点P作PD∥y轴交BC于点D，求线段PD长度的最大值；

（3）如图2，当BQ交y轴于点M，∠QBC＝∠PBC，∠BCP＝45°，求点M的坐标．

12．如图，已知二次函数的图象经过点A（3，3）、B（4，0）和原点O．P为二次函数图象上的一个动点，过点P作x轴的垂线，垂足为D（m，0），并与直线OA交于点C．

（1）求出二次函数的解析式；

（2）当点P在直线OA的上方时，求线段PC的最大值；

（3）当点P在直线OA的上方时，求△APO的最大面积．

13．如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过A（﹣3，0）、B（1，0）两点，与y轴交于点C，其顶点为D，连接AD．

（1）求抛物线的函数解析式；

（2）如图①，若点P是线段AD上一个动点，过点P作PE⊥y轴于点E，求△PAE面积S的最大值；

（3）如图②，若点M是x轴上一个动点，过M作直线MQ∥BC交抛物线于点Q，问抛物线上是否存在点Q，使以点B、C、M、Q为顶点的四边形是平行四边形？若存在，请求出点Q的坐标；若不存在，请说明理由．

14．综合与探究．

如图，抛物线y＝x2+bx+c与x轴交于A、B两点，与y轴交于C点，OA＝2，OC＝6，连接AC和BC．

（1）求抛物线的解析式；

（2）点E是第四象限内抛物线上的动点，连接CE和BE．若设E点的横坐标为t，则请你求出△BCE面积S与t之间存在怎样的函数关系；

（3）若点M是x轴上的动点，在抛物线的对称轴上是否存在点N，使以点A、C、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

15．如图，抛物线y＝ax2+bx+c与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，且当x＝0和x＝2时，y的值相等，直线y＝3x﹣7与这条抛物线交于两点，其中一点横坐标为4，另一点是这条抛物线的顶点M．

（1）求顶点M的坐标并求出这条抛物线对应的函数解析式．

（2）P为线段BM上一点（P不与点B，M重合），作PQ⊥x轴于点Q，连接PC，设OQ＝t，四边形PQAC的面积为S，求S与t的函数解析式，并直接写出t的取值范围．

（3）在线段BM上是否存在点N，使△NMC为等腰三角形？若存在，直接写出点N的坐标，若不存在，说明理由．

16．如图①，在平面直角坐标系中，矩形ABCO的顶点O为坐标原点，点A在x轴上，点C在y轴上，点B的坐标为（3，4），点C的坐标为（0，4），抛物线y＝﹣x2+bx+c经过点B和点C，连接AC，点M是线段AC上一动点，连接OM，点N在线段AM上（不与点M重合）连接ON并延长交边AB于点E，连接ME．

（1）求抛物线的表达式；

（2）当ON时，求线段CN的长；

（3）在（2）的条件下，将△MOE绕点O逆时针旋转得到△M1OE1，使OE1落在线段OC上，如图②，当时，过点C作CP∥M1E1交抛物线于点P（点C除外），请直接写出点P的横坐标．

17．二次函数y＝（m﹣1）6x+9的图象与x轴交于点A和点B，以AB为边在x轴下方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．

（1）求出m的值并求出点A、点B的坐标．

（2）当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，求出这个最大值；

（3）是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．

18．如图，抛物线y＝﹣x2﹣2x+3的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．

（1）求点A、B、C的坐标；

（2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM．如图，点P在点Q左边，试用含m的式子表示矩形PQNM的周长；

（3）当矩形PQNM的周长最大时，m的值是多少？并求出此时的△AEM的面积．

19．如图，抛物线y＝ax2+2ax+c的图象与x轴交于A、B两点（点A在点B的左边）AB＝4，与y轴交于点C，OC＝OA，点D为抛物线的顶点．

（1）求抛物线的解析式；

（2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；

（3）已知H（0，﹣1），点G在抛物线上，连HG，直线HG⊥CF，垂足为F，若BF＝BC，求点G的坐标．

20．如图，已知抛物线与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C（0，3）．

（1）求抛物线的解析式；

（2）点D是第一象限内抛物线上的一个动点（与点C、B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD、CD．设点D的横坐标为m，△BCD的面积为S．求S关于m的函数解析式及自变量m的取值范围，并求出S的最大值；

（3）已知M为抛物线对称轴上一动点，若△MBC是以BC为直角边的直角三角形，请直接写出点M的坐标．