2022年中考数学三轮复习：圆

这是一份2022年中考数学三轮复习：圆，共46页。
2022年中考数学三轮复习：圆
一．选择题（共16小题）
1．如图，在矩形ABCD中，已知AB＝3，BC＝4，点P是BC边上一动点（点P不与B，C重合），连接AP，作点B关于直线AP的对称点M，则线段MC的最小值为（　　）

A．2 B． C．3 D．
2．如图，AB为⊙O的直径，弦CD⊥AB于点F，OE⊥AC于点E，若OE＝3，OB＝5，则CD的长度是（　　）

A．9.6 B．4 C．5 D．10
3．如图，AB是⊙O的直径，弦CD⊥OA于点E，连结OC，OD．若⊙O的半径为m，∠AOD＝∠α，则下列结论一定成立的是（　　）

A．OE＝m•tanα B．CD＝2m•sinα
C．AE＝m•cosα D．S△COD＝m2•sinα
4．“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，CD为⊙O的直径，弦AB⊥CD，垂足为点E，CE＝1寸，AB＝10寸，则直径CD的长度是（　　）

A．12寸 B．24寸 C．13寸 D．26寸
5．如图，AB是⊙O的弦，且AB＝6，点C是弧AB中点，点D是优弧AB上的一点，∠ADC＝30°，则圆心O到弦AB的距离等于（　　）

A． B． C． D．
6．如图，在平面直角坐标系中，已知⊙A经过点E、B、O．C且点O为坐标原点，点C在y轴上，点E在x轴上，A（﹣3，2），则cos∠OBC的值为（　　）

A． B． C． D．
7．如图，四边形ABCD是⊙O的内接四边形，∠B＝90°，∠BCD＝120°，AB＝2，CD＝1，则AD的长为（　　）

A．2﹣2 B．3﹣ C．4﹣ D．2
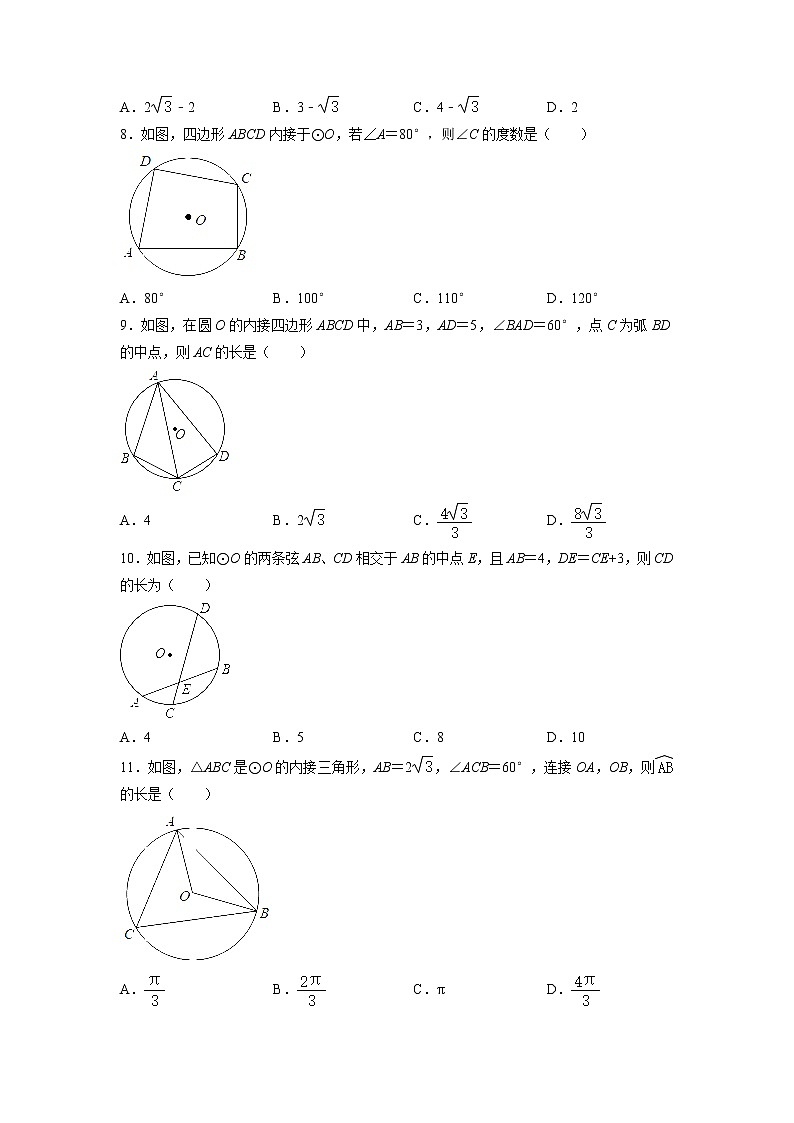
8．如图，四边形ABCD内接于⊙O，若∠A＝80°，则∠C的度数是（　　）

A．80° B．100° C．110° D．120°
9．如图，在圆O的内接四边形ABCD中，AB＝3，AD＝5，∠BAD＝60°，点C为弧BD的中点，则AC的长是（　　）

A．4 B．2 C． D．
10．如图，已知⊙O的两条弦AB、CD相交于AB的中点E，且AB＝4，DE＝CE+3，则CD的长为（　　）

A．4 B．5 C．8 D．10
11．如图，△ABC是⊙O的内接三角形，AB＝2，∠ACB＝60°，连接OA，OB，则的长是（　　）

A． B． C．π D．
12．如图，直角坐标系中，以5为半径的动圆的圆心A沿x轴移动，当⊙A与直线l：y＝x只有一个公共点时，点A的坐标为（　　）

A．（﹣12，0） B．（﹣13，0） C．（±12，0） D．（±13，0）
13．如图，在边长为2的正方形ABCD中，AE是以BC为直径的半圆的切线，则图中阴影部分的面积为（　　）

A． B．π﹣2 C．1 D．
14．如图，在△ABC中，AB＝6，以点A为圆心，3为半径的圆与边BC相切于点D，与AC，AB分别交于点E和点G，点F是优弧GE上一点，∠CDE＝18°，则∠GFE的度数是（　　）

A．50° B．48° C．45° D．36°
15．如图，四边形ABCD内接于⊙O，AB＝BC．AT是⊙O的切线，∠BAT＝55°，则∠D等于（　　）

A．110° B．115° C．120° D．125°
16．如图，正方形ABCD内接于⊙O，点P在上，则∠BPC的度数为（　　）

A．30° B．45° C．60° D．90°
二．填空题（共3小题）
17．如图，AB是⊙O的直径，CD是⊙O的弦，∠CAB＝55°，则∠D的度数是 　 　．

18．如图，在Rt△ABC中，∠ABC＝90°，∠A＝32°，点B、C在⊙O上，边AB、AC分别交⊙O于D、E两点，点B是的中点，则∠ABE＝　 　．

19．如图，△ABC内接于⊙O，∠A＝50°，点D是BC的中点，连接OD，OB，OC，则∠BOD＝　 　．

三．解答题（共15小题）
20．如图，AB为⊙O的弦，D，C为的三等分点，延长DC至点E，AC∥BE．
（1）求证：∠A＝∠E；
（2）若BC＝3，BE＝5，求CE的长．

21．如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED．
（1）求证：BD＝ED；
（2）若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．

22．如图，四边形ABCD内接于圆，∠ABC＝60°，对角线BD平分∠ADC．
（1）求证：△ABC是等边三角形；
（2）过点B作BE∥CD交DA的延长线于点E，若AD＝2，DC＝3，求△BDE的面积．

23．如图，四边形ABCD内接于⊙O，AC是⊙O的直径，作DE∥BC，交BO的延长线于点E，且BE平分∠ABD．
（1）求证：四边形BCDE是平行四边形；
（2）若AD＝8，tan∠BDE＝，求AC的长与▱BCDE的周长．

24．如图，△ABC内接于⊙O（∠ACB＞90°），连接OA，OC．记∠BAC＝α，∠BCO＝β，∠BAO＝γ．
（1）探究α与β之间的数量关系，并证明．
（2）设OC与AB交于点D，⊙O半径为1，
①若β＝γ+45°，AD＝2OD，求由线段BD，CD，弧BC围成的图形面积S．
②若α+2γ＝90°，设sinα＝k，用含k的代数式表示线段OD的长．

25．如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O的直径．

26．如图，四边形ABCD内接于⊙O，AC是⊙O的直径，过点B作BE⊥AD，垂足为点E，AB平分∠CAE．
（1）判断BE与⊙O的位置关系，并说明理由；
（2）若∠ACB＝30°，⊙O的半径为6，请求出图中阴影部分的面积．

27．如图，AB是⊙O的直径，点E、F在⊙O上，且＝2，连接OE、AF，过点B作⊙O的切线，分别与OE、AF的延长线交于点C、D．
（1）求证：∠COB＝∠A；
（2）若AB＝6，CB＝4，求线段FD的长．

28．如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过点D作DE⊥MN于点E．
（1）求证：DE是⊙O的切线；
（2）若DE＝4cm，AE＝3cm，求⊙O的半径．

29．如图，PA与⊙O相切于点A，过点A作AB⊥OP，垂足为C，交⊙O于点B．连接PB，AO，并延长AO交⊙O于点D，与PB的延长线交于点E．
（1）求证：PB是⊙O的切线；
（2）若OC＝3，AC＝4，求sinE的值．

30．如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F．
（1）求证：EF是⊙O的切线；
（2）若AC＝4，CE＝2，求的长度．（结果保留π）

31．已知如图，△ABC中AB＝AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于G，交AB于点F，FB恰为⊙O的直径．
（1）求证：AE与⊙O相切；
（2）当BC＝6，cosC＝，求⊙O的直径．

32．如图，PA是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E．过A点作AB⊥PO于点D，交⊙O于B，连接BC，PB．
（1）求证：PB是⊙O的切线；
（2）求证：E为△PAB的内心；
（3）若cos∠PAB＝，BC＝1，求PO的长．

33．如图，⊙O是△ABC的外接圆，点E是△ABC的内心，AE的延长线交BC于点F，交⊙O于点D，连接BD，BE．
（1）求证：DB＝DE；
（2）若AE＝3，DF＝4，求DB的长．

34．如图，四边形ABCD中，AD∥BC，∠BAD＝90°，CB＝CD，连接BD，以点B为圆心，BA长为半径作⊙B，交BD于点E．
（1）试判断CD与⊙B的位置关系，并说明理由；
（2）若AB＝2，∠BCD＝60°，求图中阴影部分的面积．


2022年中考数学三轮复习：圆
参考答案与试题解析
一．选择题（共16小题）
1．如图，在矩形ABCD中，已知AB＝3，BC＝4，点P是BC边上一动点（点P不与B，C重合），连接AP，作点B关于直线AP的对称点M，则线段MC的最小值为（　　）

A．2 B． C．3 D．
【解答】解：连接AM，

∵点B和M关于AP对称，
∴AB＝AM＝3，
∴M在以A圆心，3为半径的圆上，
∴当A，M，C三点共线时，CM最短，
∵AC＝，AM＝AB＝3，
∴CM＝5﹣3＝2，
故选：A．
2．如图，AB为⊙O的直径，弦CD⊥AB于点F，OE⊥AC于点E，若OE＝3，OB＝5，则CD的长度是（　　）

A．9.6 B．4 C．5 D．10
【解答】解：∵OE⊥AC，
∴AE＝EC，
∵AB⊥CD，
∴∠AFC＝∠AEO＝90°，
∵OE＝3，OB＝5，
∴AE＝，
∴AC＝8，
∵∠A＝∠A，∠AEO＝∠AFC，
∴△AEO∽△AFC，
∴，即：，
∴，
∵CD⊥AB，
∴CD＝2CF＝＝9.6．
故选：A．
3．如图，AB是⊙O的直径，弦CD⊥OA于点E，连结OC，OD．若⊙O的半径为m，∠AOD＝∠α，则下列结论一定成立的是（　　）

A．OE＝m•tanα B．CD＝2m•sinα
C．AE＝m•cosα D．S△COD＝m2•sinα
【解答】解：∵AB是⊙O的直径，弦CD⊥OA于点E，∴DE＝CD，
在Rt△EDO中，OD＝m，∠AOD＝∠α，
∴tanα＝，
∴OE＝＝，
故选项A不符合题意；
∵AB是⊙O的直径，CD⊥OA，
∴CD＝2DE，
∵⊙O的半径为m，∠AOD＝∠α，
∴DE＝OD•sinα＝m•sinα，
∴CD＝2DE＝2m•sinα，
故选项B正确，符合题意；
∵cosα＝，
∴OE＝OD•cosα＝m•cosα，
∵AO＝DO＝m，
∴AE＝AO﹣OE＝m﹣m•cosα，
故选项C不符合题意；
∵CD＝2m•sinα，OE＝m•cosα，
∴S△COD＝CD×OE＝×2m•sinα×m•cosα＝m2sinα•cosα，
故选项D不符合题意；
故选：B．
4．“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，CD为⊙O的直径，弦AB⊥CD，垂足为点E，CE＝1寸，AB＝10寸，则直径CD的长度是（　　）

A．12寸 B．24寸 C．13寸 D．26寸
【解答】解：连接OA，
∵AB⊥CD，且AB＝10寸，
∴AE＝BE＝5寸，
设圆O的半径OA的长为x，则OC＝OD＝x，
∵CE＝1，
∴OE＝x﹣1，
在直角三角形AOE中，根据勾股定理得：
x2﹣（x﹣1）2＝52，化简得：x2﹣x2+2x﹣1＝25，
即2x＝26，
∴CD＝26（寸）．
故选：D．

5．如图，AB是⊙O的弦，且AB＝6，点C是弧AB中点，点D是优弧AB上的一点，∠ADC＝30°，则圆心O到弦AB的距离等于（　　）

A． B． C． D．
【解答】解：如图，

连接OA、OC，OC交AB于点E，
∵点C是弧AB中点，AB＝6，
∴OC⊥AB，且AE＝BE＝3，
∵∠ADC＝30°，
∴∠AOC＝2∠ADC＝60°，
∴OE＝AE＝，
故圆心O到弦AB的距离为．
故选：C．
6．如图，在平面直角坐标系中，已知⊙A经过点E、B、O．C且点O为坐标原点，点C在y轴上，点E在x轴上，A（﹣3，2），则cos∠OBC的值为（　　）

A． B． C． D．
【解答】解：过A作AM⊥x轴于M，AN⊥y轴于N，连接EC，
∵∠COE＝90°，
∴EC是⊙A的直径，即EC过O，
∵A（﹣3，2），
∴OM＝3，ON＝2，
∵AM⊥x轴，x轴⊥y轴，
∴AM∥OC，
同理AN∥OE，
∴N为OC中点，M为OE中点，
∴OE＝2AN＝6，OC＝2AM＝4，
由勾股定理得：EC＝＝2，
∵∠OBC＝∠OEC，
∴cos∠OBC＝cos∠OEC＝＝＝，
故选：B．
7．如图，四边形ABCD是⊙O的内接四边形，∠B＝90°，∠BCD＝120°，AB＝2，CD＝1，则AD的长为（　　）

A．2﹣2 B．3﹣ C．4﹣ D．2
【解答】解：延长AD、BC交于E，
∵∠BCD＝120°，
∴∠A＝60°，
∵∠B＝90°，
∴∠ADC＝90°，∠E＝30°，
在Rt△ABE中，AE＝2AB＝4，
在Rt△CDE中，DE＝＝，
∴AD＝AE﹣DE＝4﹣，
故选：C．

8．如图，四边形ABCD内接于⊙O，若∠A＝80°，则∠C的度数是（　　）

A．80° B．100° C．110° D．120°
【解答】解：∵四边形ABCD内接于⊙O，
∴∠A+∠C＝180°，
∵∠A＝80°，
∴∠C＝100°，
故选：B．
9．如图，在圆O的内接四边形ABCD中，AB＝3，AD＝5，∠BAD＝60°，点C为弧BD的中点，则AC的长是（　　）

A．4 B．2 C． D．
【解答】解：∵A、B、C、D四点共圆，∠BAD＝60°，
∴∠BCD＝180°﹣60°＝120°，
∵∠BAD＝60°，AC平分∠BAD，
∴∠CAD＝∠CAB＝30°，
如图1，
将△ACD绕点C逆时针旋转120°得△CBE，
则∠E＝∠CAD＝30°，BE＝AD＝5，AC＝CE，
∴∠ABC+∠EBC＝（180°﹣∠CAB﹣∠ACB）+（180°﹣∠E﹣∠BCE）＝180°，
∴A、B、E三点共线，
过C作CM⊥AE于M，
∵AC＝CE，
∴AM＝EM＝×（5+3）＝4，
在Rt△AMC中，AC＝＝＝；
故选：D．

10．如图，已知⊙O的两条弦AB、CD相交于AB的中点E，且AB＝4，DE＝CE+3，则CD的长为（　　）

A．4 B．5 C．8 D．10
【解答】解：设CE＝x，则DE＝3+x．
根据相交弦定理，得x（x+3）＝2×2，
x＝1或x＝﹣4（不合题意，应舍去）．
则CD＝3+1+1＝5．
故选：B．
11．如图，△ABC是⊙O的内接三角形，AB＝2，∠ACB＝60°，连接OA，OB，则的长是（　　）

A． B． C．π D．
【解答】解：过点O作OD⊥AB于D，
则AD＝DB＝AB＝，
由圆周角定理得：∠AOB＝2∠ACB＝120°，
∴∠AOD＝60°，
∴OA＝＝＝2，
∴的长＝＝，
故选：D．

12．如图，直角坐标系中，以5为半径的动圆的圆心A沿x轴移动，当⊙A与直线l：y＝x只有一个公共点时，点A的坐标为（　　）

A．（﹣12，0） B．（﹣13，0） C．（±12，0） D．（±13，0）
【解答】解：当⊙A与直线l：y＝x只有一个公共点时，直线l与⊙A相切，
设切点为B，过点B作BE⊥OA于点E，如图，

∵点B在直线y＝x上，
∴设B（m，m），
∴OE＝﹣m，BE＝﹣m．
在Rt△OEB中，tan∠AOB＝．
∵直线l与⊙A相切，
∴AB⊥BO．
在Rt△OAB中，tan∠AOB＝．
∵AB＝5，
∴OB＝12．
∴OA＝．
∴A（﹣13，0）．
同理，在x轴的正半轴上存在点（13，0）．
综上所述，点A的坐标为（±13，0）．
故选：D．
13．如图，在边长为2的正方形ABCD中，AE是以BC为直径的半圆的切线，则图中阴影部分的面积为（　　）

A． B．π﹣2 C．1 D．
【解答】解：假设AE与BC为直径的半圆切于点F，则AB＝AF，
∵四边形ABCD为正方形，
∴∠BCD＝90°，
∴EC与BC为直径的半圆相切，
∴EC＝EF，
∴DE＝2﹣CE，AE＝2+CE，
在Rt△ADE中，AE2＝AD2+DE2，即（2+CE）2＝22+（2﹣CE）2，
解得：CE＝，
∴DE＝2﹣＝，
∴阴影部分的面积＝22﹣×π×12﹣×2×＝，
故选：D．

14．如图，在△ABC中，AB＝6，以点A为圆心，3为半径的圆与边BC相切于点D，与AC，AB分别交于点E和点G，点F是优弧GE上一点，∠CDE＝18°，则∠GFE的度数是（　　）

A．50° B．48° C．45° D．36°
【解答】解：连接AD，∵BC与⊙A相切于点D，
∴AD⊥BC，
∴∠ADB＝∠ADC＝90°，
∵AB＝6，AG＝AD＝3，
∴AD＝AB，
∴∠B＝30°，
∴∠GAD＝60°，
∵∠CDE＝18°，
∴∠ADE＝90°﹣18°＝72°，
∵AD＝AE，
∴∠AED＝∠ADE＝72°，
∴∠DAE＝180°﹣∠ADE﹣∠AED＝180°﹣72°﹣72°＝36°，
∴∠BAC＝∠BAD+∠CAD＝60°+36°＝96°，
∴∠GFE＝GAE＝96°＝48°，
故选：B．

15．如图，四边形ABCD内接于⊙O，AB＝BC．AT是⊙O的切线，∠BAT＝55°，则∠D等于（　　）

A．110° B．115° C．120° D．125°
【解答】解：如图，连接AC，
由弦切角定理知∠ACB＝∠BAT＝55°，
∵AB＝BC，
∴∠ACB＝∠CAB＝55°，
∴∠B＝180°﹣2∠ACB＝70°，
∴∠D＝180°﹣∠B＝110°．
故选：A．

16．如图，正方形ABCD内接于⊙O，点P在上，则∠BPC的度数为（　　）

A．30° B．45° C．60° D．90°
【解答】解：连接OB、OC，如图，

∵正方形ABCD内接于⊙O，
∴所对的圆心角为90°，
∴∠BOC＝90°，
∴∠BPC＝∠BOC＝45°．
故选：B．
二．填空题（共3小题）
17．如图，AB是⊙O的直径，CD是⊙O的弦，∠CAB＝55°，则∠D的度数是 　35°　．

【解答】解：∵AB是⊙O的直径，
∴∠ACB＝90°，
∵∠CAB＝55°，
∴∠B＝90°﹣∠CAB＝35°，
∴∠D＝∠B＝35°．
故答案为：35°．
18．如图，在Rt△ABC中，∠ABC＝90°，∠A＝32°，点B、C在⊙O上，边AB、AC分别交⊙O于D、E两点，点B是的中点，则∠ABE＝　13°　．

【解答】解：如图，连接DC，
∵∠DBC＝90°，
∴DC是⊙O的直径，
∵点B是的中点，
∴∠BCD＝∠BDC＝45°，
在Rt△ABC中，∠ABC＝90°，∠A＝32°，
∴∠ACB＝90°﹣32°＝58°，
∴∠ACD＝∠ACB﹣∠BCD＝58°﹣45°＝13°＝∠ABE，
故答案为：13°．

19．如图，△ABC内接于⊙O，∠A＝50°，点D是BC的中点，连接OD，OB，OC，则∠BOD＝　50°　．

【解答】解：∵∠A＝50°，
∴∠BOC＝100°．
∵OB＝OC，
∴△OBC为等腰三角形，
又∵D为BC中点，
∴OD为BC上中线，
根据等腰三角形三线合一性质可得OD为∠BOC的平分线，
∴∠BOD＝∠BOC＝50°．
故答案为：50°
三．解答题（共15小题）
20．如图，AB为⊙O的弦，D，C为的三等分点，延长DC至点E，AC∥BE．
（1）求证：∠A＝∠E；
（2）若BC＝3，BE＝5，求CE的长．

【解答】（1）证明：
∵AC∥BE，
∴∠E＝∠ACD，
∵D，C为的三等分点，
∴＝＝，
∴∠ACD＝∠A，
∴∠E＝∠A，
（2）解：由（1）知＝＝，
∴∠D＝∠CBD＝∠A＝∠E，
∴BE＝BD＝5，BC＝CD＝3，△CBD∽△BED，
∴＝，即，
解得DE＝，
∴CE＝DE﹣CD＝﹣3＝．
21．如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED．
（1）求证：BD＝ED；
（2）若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．

【解答】（1）证明：∵四边形ABCD内接于⊙O，
∴∠A＝∠DCE，
∵∠1＝∠2，
∴＝，
∴AD＝DC，
在△ABD和△DCE中，
，
∴△ABD≌△CED（SAS），
∴BD＝ED；
（2）解：过点D作DM⊥BE于M，
∵AB＝4，BC＝6，CE＝AB，
∴BE＝BC+EC＝10，
∵BD＝ED，DM⊥BE，
∴BM＝ME＝BE＝5，
∴CM＝BC﹣BM＝1，
∵∠ABC＝60°，∠1＝∠2，
∴∠2＝30°，
∴DM＝BM•tan∠2＝5×＝，
∴tan∠DCB＝＝．

22．如图，四边形ABCD内接于圆，∠ABC＝60°，对角线BD平分∠ADC．
（1）求证：△ABC是等边三角形；
（2）过点B作BE∥CD交DA的延长线于点E，若AD＝2，DC＝3，求△BDE的面积．

【解答】（1）证明：∵四边形ABCD内接于圆．
∴∠ABC+∠ADC＝180°，
∵∠ABC＝60°，
∴∠ADC＝120°，
∵DB平分∠ADC，
∴∠ADB＝∠CDB＝60°，
∴∠ACB＝∠ADB＝60°，∠BAC＝∠CDB＝60°，
∴∠ABC＝∠BCA＝∠BAC，
∴△ABC是等边三角形．
（2）过点A作AM⊥CD，垂足为点M，过点B作BN⊥AC，垂足为点N．
∴∠AMD＝90°，
∵∠ADC＝120°，
∴∠ADM＝60°，
∴∠DAM＝30°，
∴DM＝AD＝1，AM＝＝＝，
∵CD＝3，
∴CM＝CD+DM＝1+3＝4，
∴S△ACD＝CD•AM＝×＝，
Rt△AMC中，∠AMD＝90°，
∴AC＝＝＝，
∵△ABC是等边三角形，
∴AB＝BC＝AC＝，
∴BN＝BC＝，
∴S△ABC＝×＝，
∴四边形ABCD的面积＝+＝，
∵BE∥CD，
∴∠E+∠ADC＝180°，
∵∠ADC＝120°，
∴∠E＝60°，
∴∠E＝∠BDC，
∵四边形ABCD内接于⊙O，
∴∠EAB＝∠BCD，
在△EAB和△DCB中，
，
∴△EAB≌△DCB（AAS），
∴△BDE的面积＝四边形ABCD的面积＝．
方法二
（2）∵BE∥CD，
∴∠EBD＝∠BDC，
∵∠ADB＝∠CDB＝60°，
∴∠EBD＝∠EDB＝60°，
∴△BDE是等边三角形，
又∵△ABC为等边三角形，
∴∠EBD＝∠ABC＝60°，
∴∠ABE＝∠CBD，
在△ABE和△CBD中，
，
∴△ABE≌△CBD（SAS），
∴AE＝CD＝3，
∴DE＝AE+AD＝5，
∴△BDE的面积＝＝

23．如图，四边形ABCD内接于⊙O，AC是⊙O的直径，作DE∥BC，交BO的延长线于点E，且BE平分∠ABD．
（1）求证：四边形BCDE是平行四边形；
（2）若AD＝8，tan∠BDE＝，求AC的长与▱BCDE的周长．

【解答】证明：（1）延长BE，交AD于点F，交⊙O于点G，

∵BE平分∠ABD，
∴∠ABG＝∠DBG，
∴，
∵BE是⊙O的直径，
∴BG⊥AD，
∴∠BFD＝90°，
∵AB是⊙O的直径，
∴∠ADC＝90°，
∴∠BFD+∠ADC＝180°，
∴BE∥CD，
∵DE∥BC，
∴四边形BCDE是平行四边形；
解：（2）∵DE∥BC，
∴∠BDE＝∠CBD，
∵∠CBD＝∠CAD，
∴∠BDE＝∠CAD，
∵AC为⊙O的直径，
∴∠ADC＝90°，
在Rt△ACD中，tan∠CAD＝tan∠BDE＝＝，
∴CD＝6，
∴AC＝＝10，
∴OA＝OC＝OB＝5，
∵OF是△ACD的中位线，
∴OF＝3，
∴BF＝OB+OF＝3+5＝8，
在Rt△BDF中，BD＝＝，
∵BF是AD的垂直平分线，
∴AB＝BD＝，
在Rt△ABC中，BC＝＝，
∴C▱BCDE＝＝．
24．如图，△ABC内接于⊙O（∠ACB＞90°），连接OA，OC．记∠BAC＝α，∠BCO＝β，∠BAO＝γ．
（1）探究α与β之间的数量关系，并证明．
（2）设OC与AB交于点D，⊙O半径为1，
①若β＝γ+45°，AD＝2OD，求由线段BD，CD，弧BC围成的图形面积S．
②若α+2γ＝90°，设sinα＝k，用含k的代数式表示线段OD的长．

【解答】解：（1）α与β之间的数量关系为：α+β＝90°．理由：
连接OB，如图，

∵∠BOC＝2∠BAC，∠BAC＝α，
∴∠BOC＝2α．
∵OC＝OB，
∴∠OCB＝∠OBC＝β．
∴∠BOC+∠OCB+∠OBC＝180°，
∴2α+2β＝180°．
∴α+β＝90°．
（2）①∵β＝γ+45°，α+β＝90°，
∴90°﹣α＝γ+45°．
∴α+γ＝45°．
∵∠BAC＝α，∠BAO＝γ，
∴∠OAC＝∠BAC+∠BAO＝45°．
∵OA＝OC，
∴∠OAC＝∠OCA＝45°．
∴∠AOC＝90°．
∵AD＝2OD，
∴sin∠OAD＝．
∴∠OAD＝30°．
∴∠BAC＝15°．
∴∠BOC＝2∠BAC＝30°．
∵OA＝OD，
∴∠OBA＝∠BAO＝30°．
∴∠DOB＝∠DBO＝30°，
∴DO＝DB．
过点D作DE⊥OB于点E，如图，

则OE＝EB＝OB＝．
∵tan∠DOB＝，
∴．
∴DE＝．
∴×OB•DE＝．
∵，
∴S＝S扇形OCB﹣S△DBO＝．
②∵α+2γ＝90°，α+β＝90°，
∴β＝2γ．
延长AO，交圆O于点G，连接BG，如图，

∵∠BOG＝2∠BAO＝2γ，
∴∠BOG＝∠OCB．
∵∠OBC＝∠OCB，
∴∠BOG＝∠OBC．
∴BC∥AG．
过点O作OF⊥BC于点F，则CF＝BF＝BC，∠COF＝∠BOC＝α．
∵sinα＝k，sinα＝，
∴CF＝OC•sinα＝k，
∴BC＝2k．
设OD＝x，则CD＝OC﹣OD＝1﹣x，
∵BC∥OA，
∴△DAO∽△DBC．
∴．
∴．
解得：x＝．
∴OD＝．
25．如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O的直径．

【解答】（1）证明：连接DO，如图，

∵直径所对圆周角，
∴∠ADC＝90°，
∴∠BDC＝90°，E为BC的中点，
∴DE＝CE＝BE，
∴∠EDC＝∠ECD，
又∵OD＝OC，
∴∠ODC＝∠OCD，
而∠OCD+∠DCE＝∠ACB＝90°，
∴∠EDC+∠ODC＝90°，即∠EDO＝90°，
∴DE⊥OD且OD为半径，
∴DE与⊙O相切；

（2）由（1）得，∠CDB＝90°，
∵CE＝EB，
∴DE＝BC，
∴BC＝5，
∴BD＝＝＝4，
∵∠BCA＝∠BDC＝90°，∠B＝∠B，
∴△BCA∽△BDC，
∴＝，
∴＝，
∴AC＝，
∴⊙O直径的长为．
26．如图，四边形ABCD内接于⊙O，AC是⊙O的直径，过点B作BE⊥AD，垂足为点E，AB平分∠CAE．
（1）判断BE与⊙O的位置关系，并说明理由；
（2）若∠ACB＝30°，⊙O的半径为6，请求出图中阴影部分的面积．

【解答】解：（1）BE与圆O相切．理由如下：
如图，连接BO．
∵OA＝OB，
∴∠OAB＝∠OBA．
∵AB平分∠CAE，
∴∠OAB＝∠BAE，
∴∠OBA＝∠BAE．
∵BE⊥AD，
∴∠AEB＝90°，
∴∠ABE+∠BAE＝90°，
∴∠ABE+∠OBA＝90°，
∴∠EBO＝90°，
即BE⊥OB，
又OB是⊙O的半径，
∴BE是⊙O的切线，
即BE与⊙O相切．
（2）∵∠ACB＝30°，
∴∠AOB＝60°．
又∵OA＝OB，
∴△ABO是等边三角形，
∴∠OBA＝60°，OA＝OB＝AB＝6，
∴∠ABE＝30°，
∴．
由勾股定理，得，
∴S四边形AEBO＝S△ABE+S△ABO＝，
∴．

27．如图，AB是⊙O的直径，点E、F在⊙O上，且＝2，连接OE、AF，过点B作⊙O的切线，分别与OE、AF的延长线交于点C、D．
（1）求证：∠COB＝∠A；
（2）若AB＝6，CB＝4，求线段FD的长．

【解答】（1）证明：取的中点M，连接OM、OF，
∵＝2，
∴＝＝，
∴∠COB＝∠BOF，
∵∠A＝∠BOF，
∴∠COB＝∠A；
（2）解：连接BF，如图，
∵CD为⊙O的切线，
∴AB⊥CD，
∴∠OBC＝∠ABD＝90°，
∵∠COB＝∠A，
∴△OBC∽△ABD，
∴＝，即＝，解得BD＝8，
在Rt△ABD中，AD＝＝＝10，
∵AB是⊙O的直径，
∴∠AFB＝90°，
∵∠BDF＝∠ADB，
∴Rt△DBF∽Rt△DAB，
∴＝，即＝，解得DF＝．

28．如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过点D作DE⊥MN于点E．
（1）求证：DE是⊙O的切线；
（2）若DE＝4cm，AE＝3cm，求⊙O的半径．

【解答】（1）证明：连接OD，如图1所示：
∵OA＝OD，
∴∠1＝∠2，
∵AD平分∠CAM，
∴∠2＝∠3，
∴∠1＝∠3，
∴MN∥OD，
∵DE⊥MN，
∴DE⊥OD，
∴DE是⊙O的切线；
（2）解：连接CD，如图2所示：
∵AC是⊙O的直径，
∴∠ADC＝90°，
∴AD＝＝＝5（cm），
∵DE⊥MN，
∴∠AED＝90°，
∴∠ADC＝∠AED，
又∵∠2＝∠3，
∴△ADC∽△AED，
∴，
即，
∴AC＝（cm），
∴OA＝AC＝cm，
即⊙O的半径为cm．


29．如图，PA与⊙O相切于点A，过点A作AB⊥OP，垂足为C，交⊙O于点B．连接PB，AO，并延长AO交⊙O于点D，与PB的延长线交于点E．
（1）求证：PB是⊙O的切线；
（2）若OC＝3，AC＝4，求sinE的值．

【解答】（1）证明：连接OB∵PO⊥AB，
∴AC＝BC，
∴PA＝PB
在△PAO和△PBO中

∴△PAO≌△PBO
∴∠OBP＝∠OAP＝90°
∴PB是⊙O的切线．
（2）连接BD，则BD∥PO，且BD＝2OC＝6
在Rt△ACO中，OC＝3，AC＝4
∴AO＝5
在Rt△ACO与Rt△PAO中，
∠AOC＝∠POA
∠PAO＝∠ACO＝90°
∴△ACO∼△PAO
＝
∴PO＝，PA＝
∴PB＝PA＝
在△EPO与△EBD中，
BD∥PO
∴△EPO∽△EBD
∴＝，
解得EB＝，
PE＝，
∴sinE＝＝．

另解：过BF⊥AE于点F，
则sin∠E＝sin∠OBF．
由△AOC∽△ABF，
可算出BF＝，
∴OF＝．
∴sinE＝sin∠OBF＝．



30．如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F．
（1）求证：EF是⊙O的切线；
（2）若AC＝4，CE＝2，求的长度．（结果保留π）

【解答】解：（1）如图，连接OD，

∵OA＝OD，
∴∠OAD＝∠ODA，
∵AD平分∠EAF，
∴∠DAE＝∠DAO，
∴∠DAE＝∠ADO，
∴OD∥AE，
∵AE⊥EF，
∴OD⊥EF，
∴EF是⊙O的切线；

（2）如图，作OG⊥AE于点G，连接BD，
则AG＝CG＝AC＝2，∠OGE＝∠E＝∠ODE＝90°，
∴四边形ODEG是矩形，
∴OA＝OB＝OD＝CG+CE＝2+2＝4，∠DOG＝90°，
∵∠DAE＝∠BAD，∠AED＝∠ADB＝90°，
∴△ADE∽△ABD，
∴＝，即＝，
∴AD2＝48，
在Rt△ABD中，BD＝＝4，
在Rt△ABD中，∵AB＝2BD，
∴∠BAD＝30°，
∴∠BOD＝60°，
则的长度为＝．
31．已知如图，△ABC中AB＝AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于G，交AB于点F，FB恰为⊙O的直径．
（1）求证：AE与⊙O相切；
（2）当BC＝6，cosC＝，求⊙O的直径．

【解答】（1）证明：连接OM．
∵OB＝OM，
∴∠1＝∠3，
又BM平分∠ABC交AE于点M，
∴∠1＝∠2，
∴∠2＝∠3，
∴OM∥BE．
∵AB＝AC，AE是角平分线，
∴AE⊥BC，
∴OM⊥AE，
∴AE与⊙O相切；

（2）解：设圆的半径是r．
∵AB＝AC，AE是角平分线，
∴BE＝CE＝3，∠ABC＝∠C，
又cosC＝，
∴AB＝BE÷cosB＝12，则OA＝12﹣r．
∵OM∥BE，
∴，
即，
解得r＝2.4．
则圆的直径是4.8．

32．如图，PA是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E．过A点作AB⊥PO于点D，交⊙O于B，连接BC，PB．
（1）求证：PB是⊙O的切线；
（2）求证：E为△PAB的内心；
（3）若cos∠PAB＝，BC＝1，求PO的长．

【解答】（1）证明：连接OB，
∵AC为⊙O的直径，
∴∠ABC＝90°，
∵AB⊥PO，
∴PO∥BC
∴∠AOP＝∠C，∠POB＝∠OBC，
OB＝OC，
∴∠OBC＝∠C，
∴∠AOP＝∠POB，
在△AOP和△BOP中，
，
∴△AOP≌△BOP（SAS），
∴∠OBP＝∠OAP，
∵PA为⊙O的切线，
∴∠OAP＝90°，
∴∠OBP＝90°，
∴PB是⊙O的切线；
（2）证明：连接AE，
∵PA为⊙O的切线，
∴∠PAE+∠OAE＝90°，
∵AD⊥ED，
∴∠EAD+∠AED＝90°，
∵OE＝OA，
∴∠OAE＝∠AED，
∴∠PAE＝∠DAE，即EA平分∠PAD，
∵PA、PB为⊙O的切线，
∴PD平分∠APB
∴E为△PAB的内心；
（3）解：∵∠PAB+∠BAC＝90°，∠C+∠BAC＝90°，
∴∠PAB＝∠C，
∴cos∠C＝cos∠PAB＝，
在Rt△ABC中，cos∠C＝＝＝，
∴AC＝，AO＝，
∵△PAO∽△ABC，
∴，
∴PO＝＝＝5．

33．如图，⊙O是△ABC的外接圆，点E是△ABC的内心，AE的延长线交BC于点F，交⊙O于点D，连接BD，BE．
（1）求证：DB＝DE；
（2）若AE＝3，DF＝4，求DB的长．

【解答】（1）证明：∵点E是△ABC的内心，
∴AE平分∠BAC，BE平分∠ABC，
∴∠BAD＝∠CAD，∠ABE＝∠CBE，
又∵∠CAD与∠CBD所对弧为，
∴∠CAD＝∠CBD＝∠BAD．
∴∠BED＝∠ABE+∠BAD，∠DBE＝∠CBE+∠CBD，
即∠BED＝∠DBE，
故DB＝DE．
（2）解：∵∠D＝∠D，∠DBF＝∠CAD＝∠BAD，
∴△ABD∽△BFD，
∴①，
∵DF＝4，AE＝3，设EF＝x，
由（1）可得DB＝DE＝4+x，
则①式化为，
解得：x1＝2，x2＝﹣6（不符题意，舍去），
则DB＝4+x＝4+2＝6．
34．如图，四边形ABCD中，AD∥BC，∠BAD＝90°，CB＝CD，连接BD，以点B为圆心，BA长为半径作⊙B，交BD于点E．
（1）试判断CD与⊙B的位置关系，并说明理由；
（2）若AB＝2，∠BCD＝60°，求图中阴影部分的面积．

【解答】解：（1）过点B作BF⊥CD，垂足为F，
∵AD∥BC，
∴∠ADB＝∠CBD，
∵CB＝CD，
∴∠CBD＝∠CDB，
∴∠ADB＝∠CDB．
在△ABD和△FBD中，
，
∴△ABD≌△FBD（AAS），
∴BF＝BA，则点F在圆B上，
∴CD与⊙B相切；

（2）∵∠BCD＝60°，CB＝CD，
∴△BCD是等边三角形，
∴∠CBD＝60°
∵BF⊥CD，
∴∠ABD＝∠DBF＝∠CBF＝30°，
∴∠ABF＝60°，
∵AB＝BF＝，
∴AD＝DF＝AB·tan30°＝2，
∴阴影部分的面积＝S△ABD﹣S扇形ABE
＝
＝