人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.1 空间向量及其运算课前预习课件ppt

课题名

空间向量的数量积

课型

新授课

教学目标

1.学习空间向量的夹角、空间向量的数量积概念；

2.学习空间向量数量积的运算律；

3.能利用空间向量数量积作为工具解决几何中的有关问题.

教学重难点

重点：空间向量的数量积运算；

难点：用空间向量数量积作为工具解决几何中的有关问题.

为了更好地突破难点，在素养篇里配备了问题2、问题3，在思维篇里配备了问题1、问题2，引导学生分四步突破难点：第一步，将几何目标向量化；第二步，选用适当的基底作为桥梁，用基向量将目标表示出来；第三步，利用向量的数量积运算律，对目标加以运算；第四步，将运算结果翻译成几何结论.

教学环节

教学过程

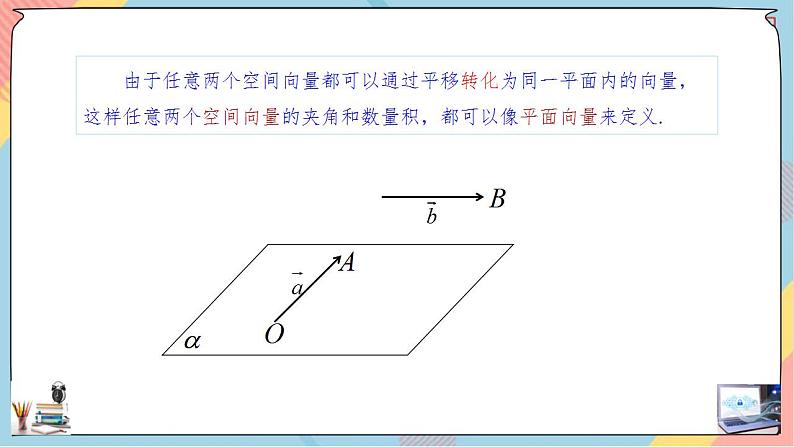
课堂导入

前面已经学习过平面向量.由于任意两个空间向量都可以通过平移转化为同一平面内的向量，这样任意两个空间向量的夹角和数量积，都可以像平面向量来定义.

课

程

学

习

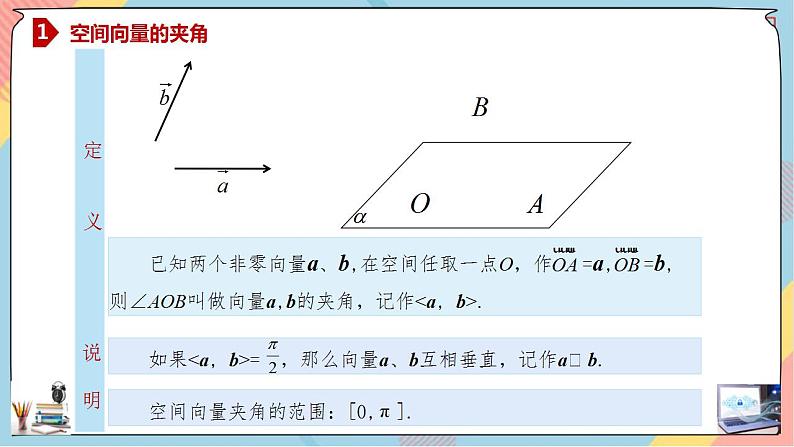
一、空间向量的夹角

已知两个非零向量a、b,在空间任取一点O，作   =a,   =b,

则∠AOB叫做向量a,b的夹角，记作<a, b>.

   如果<a, b>= ，那么向量a、b互相垂直，记作a⟂b.

空间向量夹角的范围：[0,π].

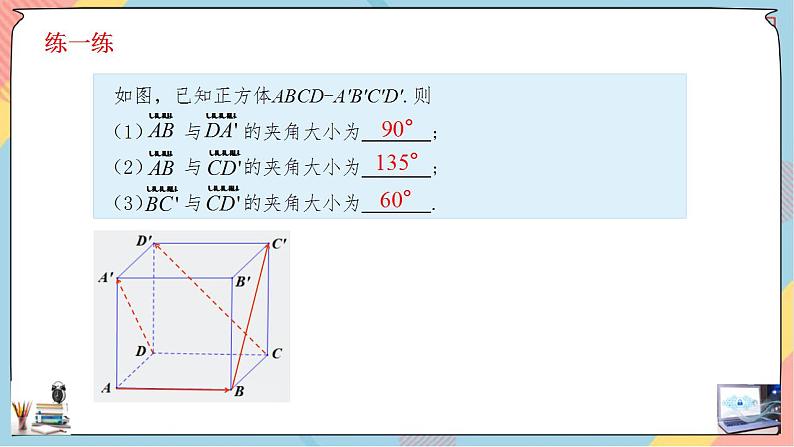
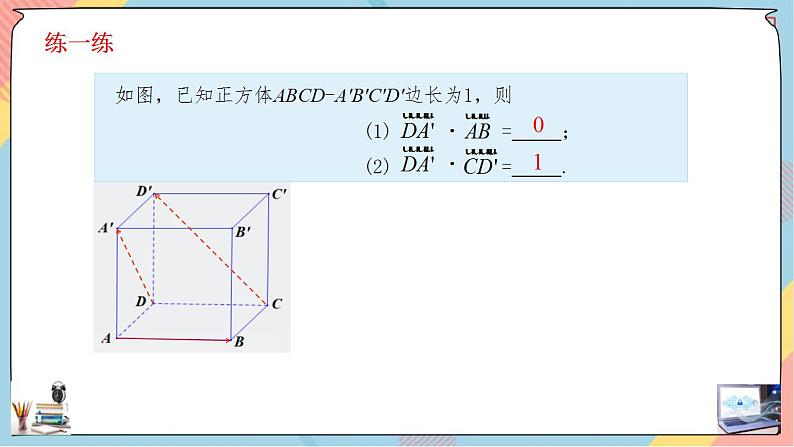
巩固练习1

二、空间向量的数量积

空间任意两个非零向量a和b，则 |a||b|cosθ叫做a与 b 的数量积，记作a•b，即

            a•b=|a||b|cosθ

特别地，零向量与任意向量的数量积为0.

a⊥b       a•b=0

    a•a=|a||a|cos0=|a|2

巩固练习2

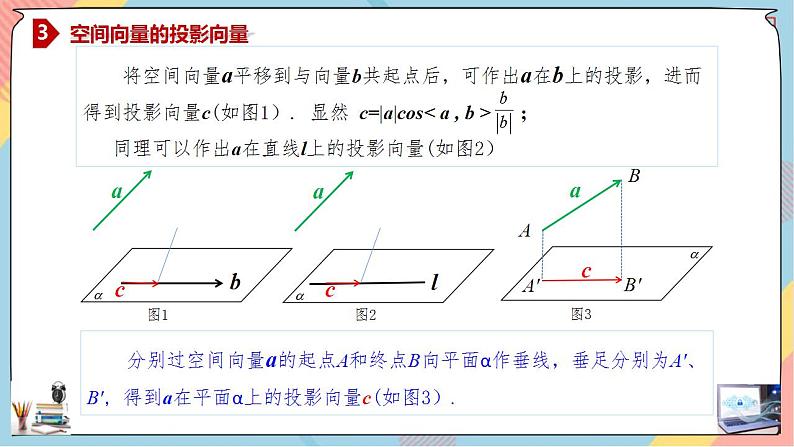
三、空间向量的投影向量

将空间向量a平移到与向量b共起点后，可作出a在b上的投影，进而得到投影向量c(如图1）. 显然 c=|a|cos< a , b >      ;  

    同理可以作出a在直线l上的投影向量

分别过空间向量a的起点A和终点B向平面α作垂线，垂足分别为A'、B', 得到a在平面α上的投影向量c

巩固练习3

四、空间向量数量积的运算律

  (λa)•b=λ(a•b), λ∈R；

  a•b=b•a(交换律)；

  a•(b+c)=a•b+a•c(分配律)

巩固练习4

五、核心素养提升

六、思维方法训练

  问题1

问题2

课堂

小结

一、本节课新知识回顾（由师生共同完成）

二、本节课核心素养方法回顾

三、本节课用到的数学思想方法回顾

板书设计

教学反思