初中苏科版11.4 解一元一次不等式课文ppt课件

这是一份初中苏科版11.4 解一元一次不等式课文ppt课件，共24页。PPT课件主要包含了不等式的性质1，不等式的性质2，不等式的性质3，不等式的性质12，课后回顾，用数轴表示不等式解集等内容，欢迎下载使用。

性质一：不等式的两边都加上(或减去)同一个数（或式子），不等号方向不变。
表示为：如果a>b，那么a±c>b±c
性质二：不等式的两边乘(或除)同一个正数，不等号方向不变。
性质三：不等式的两边乘(或除)同一个负数，不等号方向发生改变。
学习目标1、掌握不等式的性质。2、运用不等式性质解不等式。3、用数轴表示不等式的解集。重点用数轴表示不等式的解集。难点运用不等式的性质解不等式。
解：根据不等式的性质1，不等式两边都加8，不等号的方向不变,得x-8+8﹥26+8， 即x﹥34.
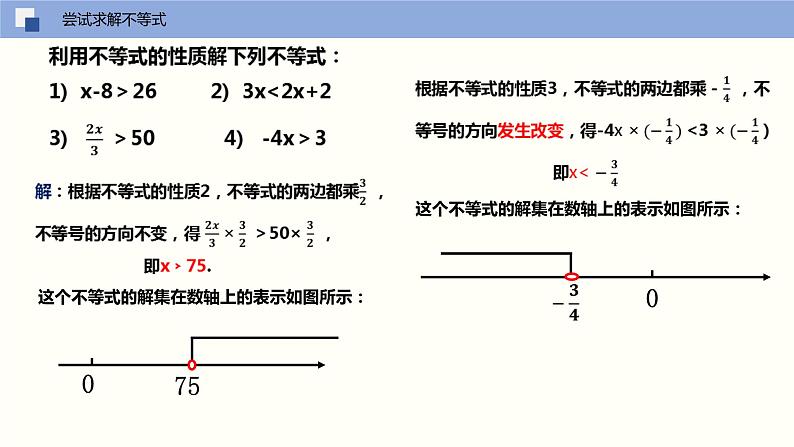
这个不等式的解集在数轴上的表示如图所示：　
解：根据不等式的性质1，不等式两边都减去2x，不等号的方向不变，得：3x-2x﹤2x+2-2x 即x﹤2
你能利用数轴表示不等式的解集吗？
这个不等式的解集在数轴上的表示如图所示：
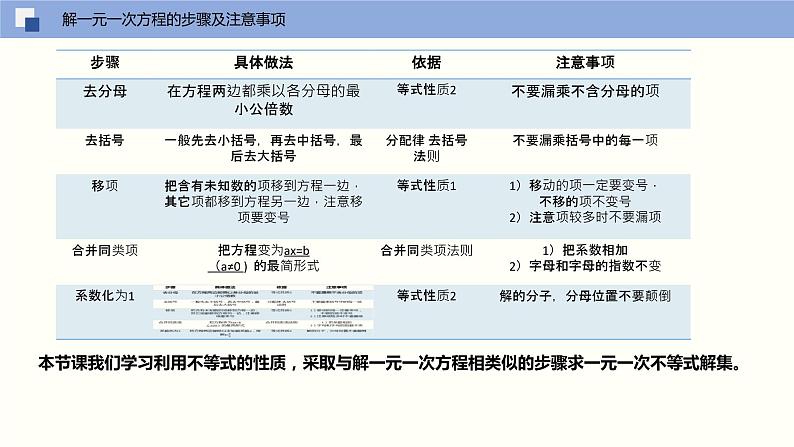
解一元一次方程的步骤及注意事项
本节课我们学习利用不等式的性质，采取与解一元一次方程相类似的步骤求一元一次不等式解集。
解：去括号，得 2x+2<3
移项，得 2x<3-2
合并同类项，得 2x<1
2）去分母，得 3（x+2）≥2（2x-1）
去括号，得 3x+6≥4x-2
移项，得 3x-4x≥-2-6
合并同类项，得 -x≥-8
系数化为1，得 x≤8
注意：不等号方向发生变化
解一元一次方程，要根据等式的性质，将方程逐步化为x=a的形式；
而解一元一次不等式，则要根据不等式的性质，将不等式逐步化为x>a或x系数化为1，得 x<3
解：去分母得：5（2x+1）≤3（3x-2）+15，去括号得：10x+5≤9x-6+15，移项得：10x-9x≤-5-6+15，合并同类项得x≤4，∴不等式的非负整数解为0、1、2、3、4．
利用不等式的性质解不等式
根据不等式的基本性质，把下列不等式化成“x>a”或“x4x+8 2）x+2<-1
解：（1）根据不等式性质1，不等式两边都减4x，不等号的方向不变， 得5x-4x>4x+8-4x，即x>8； （2）根据不等式性质1，不等式两边都减去2，不等号的方向不变， 得x+2-2<-1-2，即x<-3；
利用不等式的性质解不等式
如果关于x的不等式（1﹣k）x＞2可化为x＜﹣1，则k的值是（　　）A．1B．﹣1C．﹣3D．3
【详解】解：∵不等式（1-k）x＞2可化为x＜-1，∴1-k=-2解得：k=3．故选：D.
如果(a+1)x＜a+1的解集是x＞1，那么a的取值范围是(　　)A．a＜0B．a＜﹣1C．a＞﹣1D．a是任意有理数
【解析】根据不等式的性质3，可得答案.解：如果（a+1）x1，得a+1<0，a<-1.故选B.
不等式3x﹣3m≤﹣2m的正整数解为1，2，3，4，则m的取值范围是_____．
【详解】根据题意得：2x-(3-x)>0，整理得：3x>3，解得：x>1.故选A.
不等式(x－m)/3＞3－m的解集为x＞1，则m的值为___.
【解析】去分母得，x﹣m＞3（3﹣m），去括号得，x﹣m＞9﹣3m，移项，合并同类项得，x＞9﹣2m．∵此不等式的解集为x＞1，∴9﹣2m=1，解得m=4．
理解一元一次不等式的概念
类比解一元一次方程的方法解一元一次不等式