初中数学苏科版七年级下册11.4 解一元一次不等式图文ppt课件

这是一份初中数学苏科版七年级下册11.4 解一元一次不等式图文ppt课件，共27页。PPT课件主要包含了一元一次不等式，什么是不等式，什么是不等式的解集，不等式解集的表示方法，x-5-1，x-5≤-1，x20，x+5240，x≥5，议一议等内容，欢迎下载使用。

1.经历一元一次不等式定义的形成过程。2.会解含数字系数的一元一次不等式，并能在数轴上表示其解集。3.体会类比、化归的思想方法。
1.一元一次不等式的解法。
1.解一元一次不等式和解一元一次方程的区别和联系。
一般地，用符号“＜”(或“≤”)， “＞”(或“≥”)连接的式子叫做不等式．
一个含有未知数的不等式的所有解，组成这个不等式的解集.
1.最简不等式法； 2.用数轴来表示
这些不等式有什么特点？
我们都见过哪些含有未知数的不等式
只含有一个未知数，并且未知数的最高次数是1的不等式叫一元一次不等式.
给它们起个名字，就叫一元一次不等式吧．
怎样求一元一次不等式3x+70>100的解集？
与解方程类似．运用不等式性质．将这个不等式变形．
根据不等式的性质1，不等式的两边都减去70，得
这就是解不等式中的移项，与解方程中的移项类似．
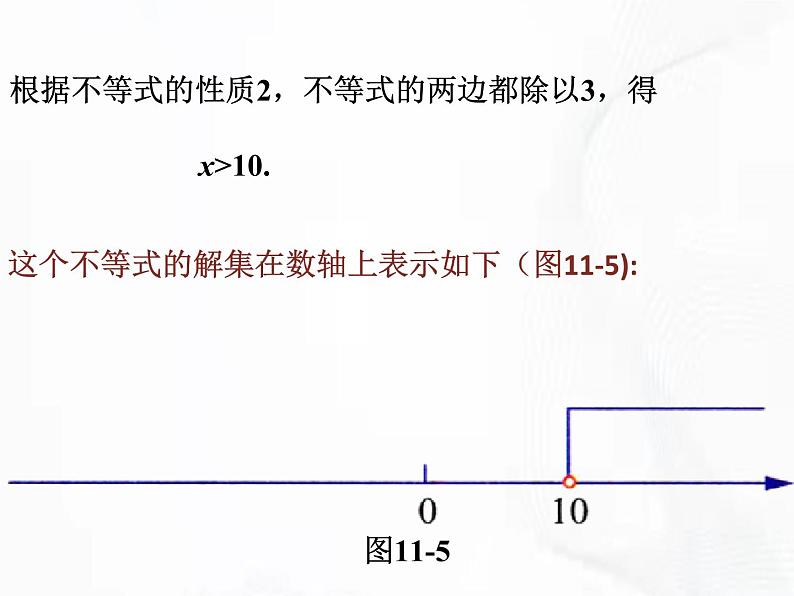
这个不等式的解集在数轴上表示如下（图11-5):
根据不等式的性质2，不等式的两边都除以3，得
解：移项，得 -2x>6-14.合并同类项，得 -2x>-8．根据不等式的性质2，不等式的两边两边都除以-2，得 x<4.这个不等式的解集在数轴上表示如下（图11-6）：
例1解不等式14-2x>6，并把它的解集在数轴上表示出来．
解：根据不等式的性质2，不等式的两边两边都乘2，得 2(2x-1) ≥3x-1.去括号，得 4x-2 ≥3x-1．移项，得 4x-3x ≥-1+2.合并同类项，得 x≥1.这个不等式的解集在数轴上表示如下（图11-7）：
例2 解不等式2x-1≥ ，并把它的解集在数轴上表示出来．
解：去分母，得 6-3(x+6) <2(2x+1).去括号，得 6-3x-18<4x+2．移项、合并同类项，得 -7x<14.两边都除以-7，得 x>-2.这个不等式的解集在数轴上表示如下（图11-8）：
例3 解不等式 ，并把它的解集在数轴上表示出来．
解下列不等式，并将解集在数轴上表示出来：（1）2x-1<4x+13;（2）2（5x+3）≤x-3（1-2x）.
解 （1）2x-1<4x+13.
2x-4x<13+1.
两边都除以-2，得x＞-7.
它在数轴上的表示如图.
（2）2（5x+3）≤x-3（1-2x）.
10x+6两边都除以3，得 x≤-3.
哇!一元一次解不等式可以移项!
解不等式3-x<2x+6，并把它的解集表示在数轴上.
3-x+x<2x+6+x
两边都除以3，得-1解不等式 ，并把它的解集表示在数轴上.
3(x-2)≥2(7-x)
两边都除以5，得 x≥4 .
要特别注意它们不一样的地方!!!
没什么新鲜的，跟解一元一次方程差不多……
例 当x在什么范围内取值时，代数式 的值比x+1的值大？
解：根据题意，x应满足不等式
1+2x>3(x+1).
将未知数系数化为1，得
即当x<-2时，代数式 的值比x+1的值大.
例3 求不等式 的正整数解.
3(x+1) ≥2(2x-1).
所以，满足这个不等式的正整数解为x=1，2，3，4，5.
解不等式，并把它的解集表示在数轴上.
一元一次不等式与一次函数
答案：当x＞ 时，y1＜y2；当x=　时，y1=y2；当x＜　时，y1＞y2．
例、若y1=-x+3，y2=3x-4，试确定当x取何值时（1）y1＜y2？（2）y1=y2？（3）y1＞y2？
根据不等式的性质1，在不等式的两边都减去70，得 3x+70-70＞100-70 合并同类项,得 3x＞30根据不等式的性质2,在不等式的两边都除以3,得 x＞10这个不等式的解集在数轴上表示如下:
计算：3x+70>100
解不等式，并在数轴上表示解集：
解：去分母，得 3（x-3）<2（2x-5），
去括号，得 3x-9<4x-10，
移项，得 3x-4x<-10+9，
合并同类项，得 -x<-1，
系数化为1，得 x>1 ．
这堂课的目标是掌握一元一次不等式的解题步骤，并学会解一元一次不等式.
你达到目标了没有？谈谈你今天的收获.