湖南省常德市汉寿县2021-2022学年八年级下学期期中义务教育阶段质量监测数学试题（含答案）

2022年上学期义务教育阶段质量监测

八年级   数学

    考号                                                           姓名___________________

考生注意：1、请考生在试题卷首填写好准考证号及姓名.

          2、请将答案填写在答题卡上，填写在试题卷上的无效.

          3、本学科试题卷共4页，六道大题，满分100 分，考试时量 120 分钟.

一、选择题（本大题共8个小题，每题4个选项中只有一个符合题意，答对得3分，共24分）

1．在平面直角坐标系中，点在（      ）

A．第一象限   B．第二象限   C．第三象限   D．第四象限

2．在中，，则该三角形为（    ）

A．锐角三角形  B．钝角三角形

C．等腰直角三角形  D．直角三角形

3．六边形的内角和为（     ）

A．  B．  C．  D.

4．下列说法正确的是（　   ）

A．正方形的对角线互相垂直且相等 B．矩形的对角线互相垂直且相等

C．菱形的对角线互相垂直且相等 D．平行四边形的对角线互相平分且相等

5． 如图所示，□OMNP的顶点坐标是，顶点坐标的是，则顶点的坐标是（      ）

A． B．          

C． D．

6．在中，，点分别是三边的中点，则的周长为（   ）

A．5 B．9 C．10 D．18

7．如图，在□ABCD中，已知，，，则的长为（     ）

A． B． 

C． D．

8．如图，在矩形中，边的长为，点分别在，上，连接，若四边形是菱形，且，则边的长为（    ）

A．    B．

C．    D．

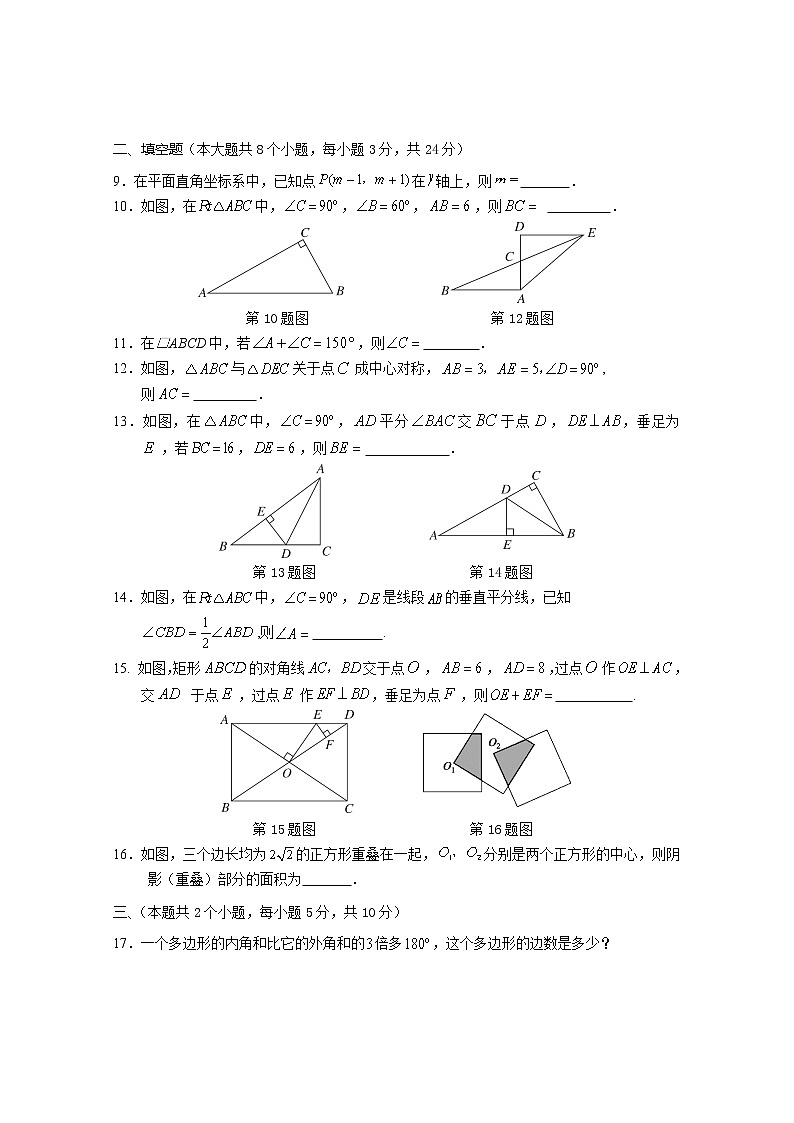
二、填空题（本大题共8个小题，每小题3分，共24分）

9．在平面直角坐标系中，已知点在轴上，则       ．

10．如图，在中，，，，则          ．

第10题图                          第12题图

11．在□ABCD中，若，则        ．

12．如图，与关于点成中心对称，,

则         ．

13．如图，在中，，平分交于点，，垂足为，若，，则            ． 

第13题图                      第14题图

14．如图，在中，，是线段的垂直平分线，已知 ,则          .

15. 如图，矩形的对角线交于点，，，过点作，交 于点，过点作，垂足为点，则           .

第15题图                      第16题图

16．如图，三个边长均为的正方形重叠在一起，分别是两个正方形的中心，则阴影（重叠）部分的面积为　   　．

三、（本题共2个小题，每小题5分，共10分）

17．一个多边形的内角和比它的外角和的倍多，这个多边形的边数是多少？

18．如图，，是上的一点，且，.

（1）求证：；（3分）

（2）是不是直角三角形？并说明理由．（2分）

四、（本题共2个小题，每小题6分，共12分）

19．如图，在边长为4的正方形中，为的中点，是上一点，且.

    （1）求的长；（4分）

（2）求证：是直角三角形.（2分）

20．如图，四边形中，，将对角线向两端分别延长至点，，使．连接，，若．证明：四边形是平行四边形．

五、（本题共2个小题，每小题7分，共14分）

21．如图，点分别在、上，分别交于点，．

（1）求证：四边形是平行四边形；（4分）

（2）已知，连接，若平分，求的长．（3分）

22．如图，在中，，垂足为，分别为边的中点，连接.

（1）若，，求的度数；（4分）

（2）若，求的周长．（3分）

六、（本题共2个小题，每小题8分，共16分）

23．如图，在中，是的角平分线，过点作交于点，过点作 交于点.

（1）求证：四边形为菱形；（4分）

（2）若，求线段的长.（4分）

24．如图，在□ABCD中，对角线与相交于点，点在上，且，

连接并延长至点，使，连接.

（1）当时，证明：四边形是矩形；（5分）

（2）当满足什么条件时，四边形是正方形？请说明理由．（3分）

2022年上学期义务教育阶段质量监测

八年级数学参考答案

一、选择题

1-4  BDCA        5-8  DBAC

二、填空题

9、        10、        11、          12、

13、      14、   15、           16、

三、17、解：设多边形的边数为，由题意得： （4分）

               解得     

这个多边形是九边形.（5分）   

18、解：∵∠1＝∠2，   ∴DE＝CE，    （1分）

在Rt△DAE和Rt△EBC中，

∴Rt△DAE≌Rt△EBC（HL）；               （3分）

（2）△CDE是直角三角形    

理由是：∵Rt△DAE≌Rt△EBC，       

∴.                        （4分）

又∵，

∴     

∴∠DEC＝ ，

∴△CED是直角三角形．                （5分）

四、19、解：（1）在中，,

由勾股定理得，

；  （2分）

在中，,，

由勾股定理得，

            （4分）

        （2）在中，,  （5分）

         在中，

         ，即

         是直角三角形                  （6分）

20、证明：在和中，

∵，∴，    （3分）

∴∠BAE=∠DCF，  

∴∠BAC=180°-∠BAE=180°-∠DCF=∠DCA， （4分）

∴AB∥CD， 又∵，             （5分）

∴四边形是平行四边形．         （6分）

五、21、解：（1） ，

，，          （1分）

又 ，

∴，                   （2分）

∴，                    （3分）

∴四边形是平行四边形；     （4分）

（2）∵平分，

∴，              （5分）

∵，∴，

∴，               （6分）

∴，又 ，

∴．                       （7分）

22、解： （1），，

，         （1分）

，分别为边，的中点， ，                                 

，            （2分）

在中，为边的中点，

，     ，      （3分）

，    ；（4分）

（2）在中，，，

由勾股定理得：，

，分别为边，的中点     

，  （5分） 

在中，，，

由勾股定理得：， 

，  （6分）

，，    ， 

为边的中点，    ，

，                        

的周长．  （7分）

六、23．解：（1）证明： ，

四边形BFDE是平行四边形，      （1分）

∵BD是的角平分线， 

∴，      （2分）

    ，

∴， ∴，      （3分）

∴平行四边形BFDE是菱形；         （4分）

（2）如图连接EF，交BD于O，

，，∴，

BD平分，  ∴．   （5分）

由（1）知，平行四边形BFDE是菱形，

则，，      （6分）

，

由勾股定理得到：，即，    

解得：，                  （7分）

．                  （8分）

24．解：（1）证明： 四边形是平行四边形，

又       

四边形是平行四边形. 

,且      （2分）

又     

，且，         

四边形是平行四边形.   （3分）

又 四边形是平行四边形， 

故   

又

                 （4分）                     

在平行四边形中，

四边形是矩形.        （5分）

（2）当满足,且时，四边形是正方形

证明：由（1）可知：当时，四边形是矩形. （6分）

在中，,点是斜边的中点，

即            （7分）

当满足,且时，四边形是正方形    （8分）