2022年湖南省湘潭县汾水乡较场中学初中学业水平模拟数学试题

       分水乡较场中学2022年学业水平数学试题(较场中学)

考试时量：120分钟    满分：120分

一、选择题（本题共8个小题，每小题有且只有一个正确答案，每小题3分，满分24分）

1、在实数，，0.101001，中，无理数的个数是（    ）

   A．0个    B．1个   C．2个   D．3个

湘潭市教育基金会在一次扶贫助残活动中，共捐款2580000元，将2580000用科学记数法表示为（   ） A、        B、      C、    D、

3、下列运算中，计算正确的是 （     ）

A．3+2=5      B．(－x2)3＝－x 6   C．(2x2y)2=2x4y2     D．(x+y2)2=x2+y4

4、如右图所示的几何体是由一些小立方块搭成的，则这个几何体的左视图是 （    ）

5、一年一度的校运会即将开始，某班为选派最优秀的选手参加比赛，特进行了一场班级选拔赛.如表记录了甲、乙、丙、丁四名跳高选手的几次跳高成绩的平均数与方差：

依表中数据，要从中选择一名成绩好且发挥稳定的选手参赛，应该选择（   ）

A．甲               B．乙            C．丙           D．丁

6、如图，点A、B、C在⊙O上，∠A=50，

则∠BOC的度数为（    ）

A．130    B．50 C．65    D．100

7、如图，过反比例函数（x＞0）的图象上任意两点A、B

分别作x轴的垂线，垂足分别为C、D，连接OA、OB，

设△AOC和△BOD的面积分别是S1、S2，可得（    ）

A、S1＞S2         B、 S1＝S2      

C、S1＜S2         D、 大小关系不能确定

8、已知二次函数y=ax²+bx+c的图像如图，它与x轴的两个交点分别是（-1,0），（3,0）对于下列命题  ① b-2a=0,  ② abc＜0,   ③ a-2b+4c＜0,  ④ 8a+c＞0                                           

 其中正确的有 (     )

   A、1个             B、2个  

C、3个         D、4个

二、填空题（本小题共8个小题，请将答案写在答题卡相应的位置上，每小题3分，满分24分）

9、分解因式：                 .

10、已知圆O1和圆O2的半径为方程的两个根，且OO=1，

则圆O1和圆O2的位置关系为                 .                          

11、如图，D，E分别在AC, AB上，且DE与BC不平行，

请填上一个合适的条件：                    使△ADE∽△ABC.

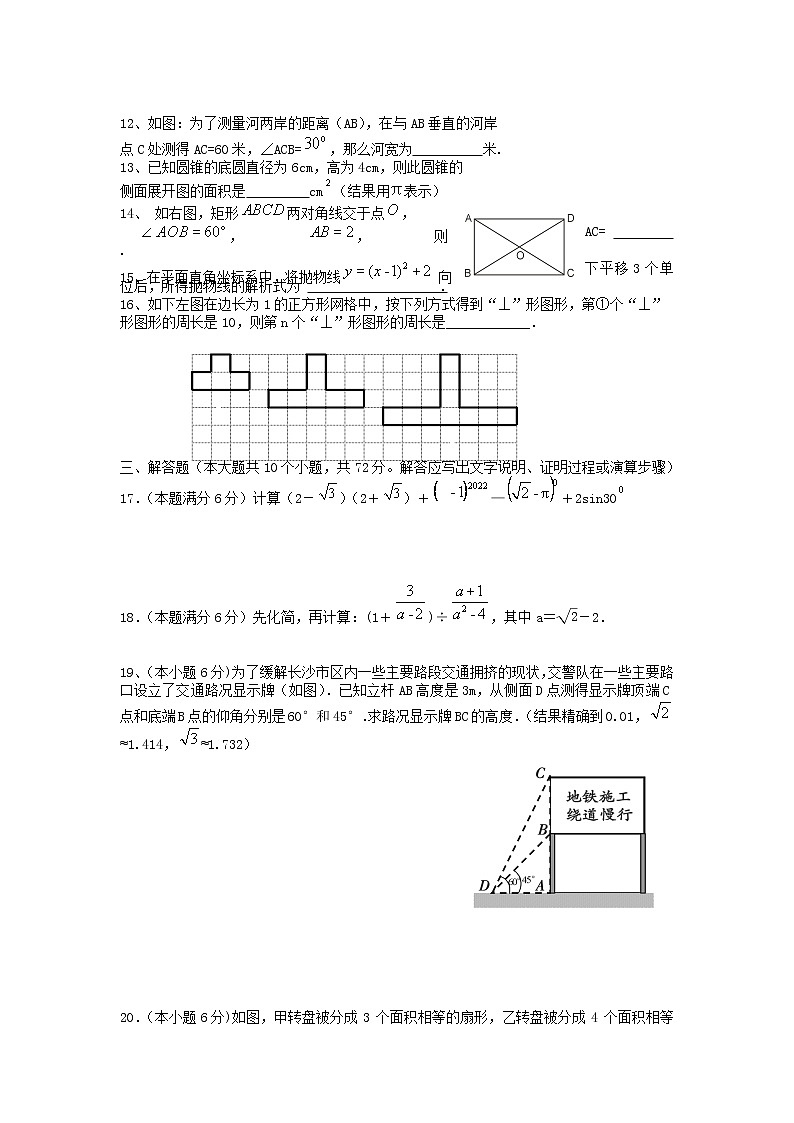
12、如图：为了测量河两岸的距离（AB），在与AB垂直的河岸

点C处测得AC=60米，∠ACB=，那么河宽为          米.

13、已知圆锥的底圆直径为6cm，高为4cm，则此圆锥的

侧面展开图的面积是         cm（结果用π表示）

14、 如右图，矩形两对角线交于点，

   ，，则AC=                .

15、在平面直角坐标系中，将抛物线 向下平移3个单位后，所得抛物线的解析式为                    .

16、如下左图在边长为1的正方形网格中，按下列方式得到“⊥”形图形，第①个“⊥”

形图形的周长是10，则第n个“⊥”形图形的周长是____________．

三、解答题（本大题共10个小题，共72分。解答应写出文字说明、证明过程或演算步骤）

17．（本题满分6分）计算（2－）（2＋）＋—＋2sin30

18．（本题满分6分）先化简，再计算：(1＋)÷，其中a＝－2．

19、（本小题6分)为了缓解长沙市区内一些主要路段交通拥挤的现状，交警队在一些主要路口设立了交通路况显示牌（如图）．已知立杆AB高度是3m，从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°．求路况显示牌BC的高度．（结果精确到0.01，≈1.414，≈1.732）

20．（本小题6分)如图，甲转盘被分成 3 个面积相等的扇形，乙转盘被分成 4 个面积相等的扇形，每一个扇形都标有相应的数字．同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为，乙转盘中指针所指区域内的数字为（当指针指在边界线上时，重转一次，直到指针指向一个区域为止）.

（1）请你用画树状图或列表格的方法，求出点落在第二象限内的概率；（用树状图或列表法求解）

（2）直接写出点(x,y)落在函数  图象上的概率.

21、（本题满分6分）如图，在△ABC中，AD平分∠BAC交BC于点D.点E、F分别在边AB、AC上，且BE=AF，FG∥AB交线段AD于点G，连接BG、EF.

（1）求证：四边形BGFE是平行四边形.

（2）若△ABG∽△AGF，AB=10，AG=6，求线段BE的长.

22、（本题满分6分）某校九年级（1）班所有学生参加2022年初中毕业生升学体育测试，根据测试评分标准，将他们的成绩进行统计后分为A、B、C、D四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：

⑴ 九年级（1）班参加体育测试的学生有_________人；

⑵ 将条形统计图补充完整；

⑶ 在扇形统计图中，等级B部分所占的百分比是        ，等级C对应的圆心角的度数为

           °；

⑷ 若该校九年级学生共有800人参加体育测试，估计达到A级和B级的学生共有_   __人

23、（本小题8分) 23、已知如图，正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内，它们的边平行于x轴或y轴，其中点A、A1、A2在直线OM上，点C、C1、C2在直线ON上，O为坐标原点，已知点A的坐标为（3，3），正方形ABCD的边长为1.

    （1）求直线ON的表达式；

（2）若点C1的横坐标为4，求正方形A1B1C1D1的边长；

（3）若正方形A2B2C2D2的边长为a，则点B2的坐标为（　　）.　

（A）（a,2a）　　（B）(2a,3a)　　（C）(3a,4a)　　（D）(4a,5a)

24．（本小题8分)开学初，小芳和小亮去学校商店购买学习用品，小芳用18元钱买了1支钢笔和3本笔记本；小亮用31元买了同样的钢笔2支和笔记本5本.

   (1)求每支钢笔和每本笔记本的价格；

   (2)为弘扬冬奥会的精神，我校举行趣味运动会，班主任拿出200元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出.

25、（本小题10分)、阅读资料：

    如图1，在平面之间坐标系中，A，B两点的坐标分别为，，由勾股定理得，所以A，B两点间的距离

我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系中，为圆上任意一点，则到原点的距离的平方为，当⊙O的半径为时，⊙O的方程可写为：．                                         

（1）问题拓展：

     如果圆心坐标为，半径为，那么⊙P的方程可以写为　        　． 

（2）综合应用：      

如图3，⊙P与轴相切于原点，点坐标为（0，6），是⊙P上一点，连接，使，作，垂足为，延长交轴于点，连接．             

①求证：是⊙P的切线；       

②是否存在到四点，，，距离都相等的点？若存在，求点坐标，并写以为圆心，以为半径的⊙的方程；若不存在，说明理由．

26、（本题满分10分）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.

如图12，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为(0，-3)，AB为半圆的直径，半圆圆心M的坐标为(1,0)，半圆半径为2.

请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围；

(2)你能求出经过点C的“蛋圆”切线的解析式吗？试试看；

(3)开动脑筋想一想，相信你能求出经过点D的“蛋圆”切线的解析式.

分水乡较场中学2022年学业水平数学试题答案

一、选择题

1-5   BBBAA        6-8     DBB

二、填空题

b（a-1)(a+1)      10、内切           11、∠AED=∠C （答案不唯一）

12、20              13、                14、4  

        16、4+6n

三、解答题

17、解：   原式=4-3+1-1+1=2

18、解：  原式=  a+2

当a=-2时，原式=-2+2=

19、解：∵在Rt△ABDZ中，∠BDA=45 

∴AD=AB=3

∵在 Rt△DAC中，∠CDA=60

∴tan∠CDA=  即 =

从而  AC=3

因此BC=AC-AB=3-3≈5.196-3≈2.196≈2.20米

20 、

或根据题意，画表格

21、（1）证明：∵FG∥AB，

∴∠BAD=∠AGF.

∵∠BAD=∠GFA,

∴∠AGF=∠GAF,

∴AF=GF.

∵BE=AF,

∴FG=BE.

又∵FG∥BE,

∴四边形BGFE为平行四边形.                           

（2）解：  ∵△ABG∽△AGF，

∴，即

∴AF=3.6.

∵BE=AF,

∴BE=3.6.                       

22、（1）50人  （2）图略    （3）40%     72    （4）560人

23 、解：（1）∵点A的坐标为（3，3），正方形ABCD的边长为1.

           ∴点B的坐标为（2，3），点C的坐标为（2，4），

              令直线ON的表达式为 y=kx，

              则4=2k，解得k=2，

               因此，直线ON的表达式为y=2x.

（2）∵点C1的横坐标为4，且在直线ON上，

             ∴C1的坐标为(4,8)，令正方形A1B1C1D1的边长为a，

              则B1的坐标为(4,8-a)，A1的坐标为(4+a,8-a)，

              ∵点A的坐标为(3,3)，易知直线OM的表达式为y=x，

              又点A1在直线OM上，则4+a=8-a ，

              解得a=2，即正方形A1B1C1D1的边长为2.

（3）B.

24、(1)设每支钢笔x元，每本笔记本y元

           依题意得：          解得：

　　　　　 答：每支钢笔3元，每本笔记本5元。

(2)设买a支钢笔，则买笔记本(48－a)本依题意得：

解得：

所以，一共有５种方案．即购买钢笔、笔记本的数量分别为：

　　　　　 ①20，28；   ② 21，27； ③22，26；  ④ 23，25；    ⑤ 24，24．

25、

26、