数学八年级下册第一章 三角形的证明2 直角三角形教学演示课件ppt

这是一份数学八年级下册第一章 三角形的证明2 直角三角形教学演示课件ppt，共18页。PPT课件主要包含了学习目标，情境导入，探索交流，几何语言，例题解析，练习巩固等内容，欢迎下载使用。

1.探索并理解直角三角形全等的判定方法“HL”．（难点）2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等．（重点）
如果已知在两个三角形中已知两边对应相等时，附加一个什么条件可以说明这两个三角形全等？
两边的夹角也对应相等时，这两个三角形全等．
如果其中一边的对角对应相等时，它们还全等吗？
如果其中一组等边的对角是直角，它们还全等吗？
已知一条直角边和斜边，求作一个直角三角形.
已知：如图，线段 a，c（a＜c），直角α.
求作：Rt△ABC，使∠C =∠α，BC=a，AB = c.
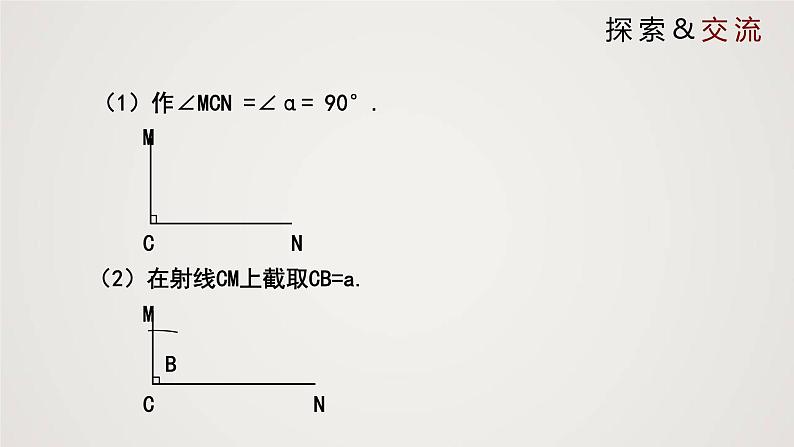
（1）作∠MCN =∠α= 90°.
（2）在射线CM上截取CB=a.
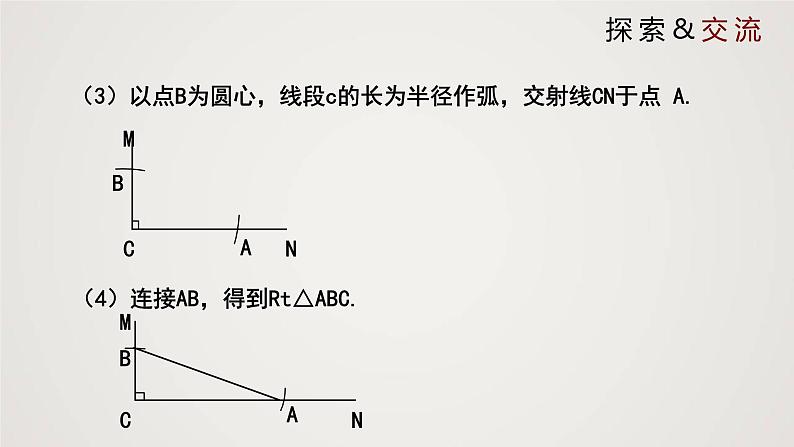
（3）以点B为圆心，线段c的长为半径作弧，交射线CN于点 A.
（4）连接AB，得到Rt△ABC.
思考：通过上面的探究，你能得出什么结论？
“斜边、直角边”判定方法
文字语言： 斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL”）.
在Rt△ABC和Rt△A′B′C′中，
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等，但是“边边”指的是斜边和一直角边，而“角”指的是直角.
定理 斜边和一条直角边分别相等的两个直角三角形全等.已知：如图,在 △ABC与△A′B′C′中，∠C＝∠C′＝90°，AB＝A′B′，求证：△ABC≌△A′B′C′
证明：在△ABC中，∵∠C=90°，∴BC2=AB2–AC2（勾股定理）.同理，B'C'2 =A'B'2–A'C'2.∵AB =A'B'，AC =A'C'，∴BC=B'C'.∴△ABC ≌△A'B'C'（SSS）.
例1.如图，AC⊥BC， BD⊥AD， AC﹦BD，求证：BC﹦AD.
证明：∵ AC⊥BC，BD⊥AD， ∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中，
∴ Rt△ABC≌Rt△BAD (HL).∴ BC﹦AD.
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
例2.如图，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF.求证： Rt△ABE≌Rt△CBF.
证明：∵∠ABC＝90°，∴∠CBF＝∠ABE＝90°.在Rt△ABE和Rt△CBF中，∵AE＝CF，AB＝CB，∴Rt△ABE≌Rt△CBF(HL)．
证明两个三角形全等，一般情况下是已知两个条件去找第三个全等条件，有以下几种情况：
(4)已知一边及其对角，只能找任意一角．
例3.如图，已知AD，AF分别是两个钝角△ABC和△ABE的高，如果AD＝AF，AC＝AE. 求证：BC＝BE.
证明：∵AD，AF分别是两个钝角△ABC和△ABE的高，且AD＝AF，AC＝AE，∴Rt△ADC≌Rt△AFE(HL)．∴CD＝EF.∵AD＝AF，AB＝AB，∴Rt△ABD≌Rt△ABF(HL)．∴BD＝BF.∴BD－CD＝BF－EF.即BC＝BE.
1.判断两个直角三角形全等的方法不正确的有（ ） A.两条直角边对应相等 B.斜边和一锐角对应相等C.斜边和一条直角边对应相等D.两个锐角对应相等
2.在Rt△ABC和Rt△A′B′C′中，∠C′=∠C=90°，∠B′=∠A，AB=B′A′，则下列结论正确的是（ ）A. AC=A′C′B. BC=B′C′C. AC=B′C′D.∠A′=∠A
3.如图，在△ABC 中，∠C＝90°，AC＝BC，AD平分∠CAB，交BC于D，DE⊥AB于E，且 AB＝6cm，则△DEB 的周长为_______cm.
4.如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证：BF=DE.