专题28第5章相似三角形之旋转相似-备战2022中考数学解题方法系统训练（全国通用）(原卷+解析)

28第5章相似三角形之旋转相似

一、单选题

1．在Rt△ABC中，∠BAC＝90°，AD是△ABC的中线，∠ADC＝45°，把△ADC沿AD对折，使点C落在C′的位置，C′D交AB于点Q，则的值为（　　）

A． B． C． D．

2．如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，给出下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④S△ABF：S四边形CDEF＝2：5，其中正确的结论有（    ）

A．1个 B．2个 C．3个 D．4个

二、填空题

3．已知正方形DEFG的顶点F在正方形ABCD的一边AD的延长线上，连结AG，CE交于点H，若，，则CH的长为________.

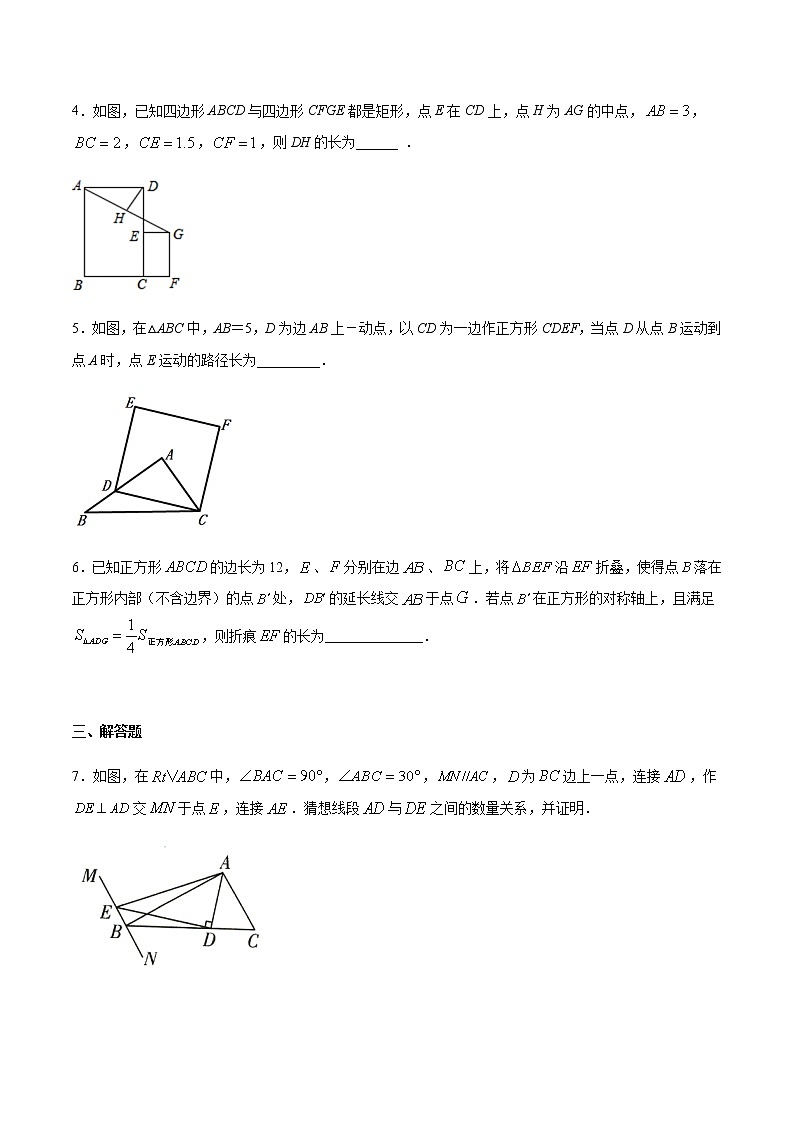
4．如图，已知四边形ABCD与四边形CFGE都是矩形，点E在CD上，点H为AG的中点，，，，，则DH的长为______ ．

5．如图，在△ABC中，AB＝5，D为边AB上－动点，以CD为一边作正方形CDEF，当点D从点B运动到点A时，点E运动的路径长为_________．

6．已知正方形的边长为12，、分别在边、上，将沿折叠，使得点落在正方形内部（不含边界）的点处，的延长线交于点．若点在正方形的对称轴上，且满足，则折痕的长为______________．

三、解答题

7．如图，在中，，，，为边上一点，连接，作交于点，连接．猜想线段与之间的数量关系，并证明．

8．已知中点分别在边、边上，连接点、点在直线同侧，连接且．

（1）点与点重合时，

①如图1，时，和的数量关系是      ；位置关系是       ；

②如图2，时，猜想和的关系，并说明理由；

（2）时，

③如图3，时，若求的长度；

④如图4，时，点分别为和的中点，若，直接写出的最小值．

9．如图1，点O为正方形ABCD 的中心，E为AB 边上一点，F为BC边上一点，△EBF的周长等于 BC 的长.

（1）求∠EOF 的度数.

（2）连接 OA、OC（如图2）.求证：△AOE∽△CFO.

（3）若OE=OF，求的值.

10．在和中，，，与在同一条直线上，点与点重合，，如图为将绕点顺时针旋转后的图形，连接，，若，求和的面积．

11．问题背景：如图（1），已知，求证：；

尝试应用：如图（2），在和中，，，与相交于点．点在边上，，求的值；

拓展创新：如图（3），是内一点，，，，，直接写出的长．

12．在中，，CD是中线，，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AE交于点M，DE与BC交于点N．

（1）如图1，若，求证：；

（2）如图2，在绕点D旋转的过程中，试证明恒成立；

（3）若，，求DN的长．

13．△ABE内接于⊙O，C在劣弧AB上，连CO交AB于D，连BO，∠COB＝∠E．

（1）如图1，求证：CO⊥AB；

（2）如图2，BO平分∠ABE，求证：AB＝BE；

（3）如图3，在(2)条件下，点P在OC延长线上，连PB，ET⊥AB于T，∠P＝2∠AET，ET＝18，OP＝25，求⊙O半径的长．

14．如图，四边形ABCD和四边形AEFG都是正方形，C，F，G三点在一直线上，连接AF并延长交边CD于点M．

（1）求证：△MFC∽△MCA；

（2）求的值，

（3）若DM＝1，CM＝2，求正方形AEFG的边长．

15．如图1，若点P是△ABC内一点，且有∠PBC=∠PCA=∠PAB，则称点P是△ABC的“等角点”

（1）如图1，∠ABC=70°，则∠APB=    

（2）如图2，在△ABC中，∠ACB=90°，点P是△ABC的“等角点”， 若∠BAC=45°

①求的值；

②求tan∠PBC的值；

16．如图，在中，∠AC8=90°，∠BAC=a，点D在边AC上（不与点A、C重合）连接BD，点K为线段BD的中点，过点D作于点E，连结CK，EK，CE，将△ADE绕点A顺时针旋转一定的角度（旋转角小于90度)

(1)如图1．若a=45，则的形状为__________________；

(2)在（1)的条件下，若将图1中的三角形ADE绕点A旋转，使得D，E，B三点共线，点K为线段BD的中点，如图2所示，求证：；

(3)若三角形ADE绕点A旋转至图3位置时，使得D，E，B三点共线，点K仍为线段BD的中点，请你直接写出BE，AE，CK三者之间的数量关系（用含a的三角函数表示）

17．如图，⊙O是△ABC的外接圆，AB为⊙O的直径，过点A作AD平分∠BAC交⊙O于点D，过点D作BC的平行线分别交AC、AB的延长线于点E、F，DG⊥AB于点G，连接BD．

(1)求证：△AED∽△DGB；

(2)求证：EF是⊙O的切线；

(3)若，OA＝4，求劣弧的长度(结果保留π)．

18．如图1，抛物线y＝a（x+2）（x﹣6）（a＞0）与x轴交于C，D两点（点C在点D的左边），与y轴负半轴交于点A．

（1）若△ACD的面积为16．

①求抛物线解析式；

②S为线段OD上一点，过S作x轴的垂线，交抛物线于点P，将线段SC，SP绕点S顺时针旋转任意相同的角到SC1，SP1的位置，使点C，P的对应点C1，P1都在x轴上方，C1C与P1S交于点M，P1P与x轴交于点N．求的最大值；

（2）如图2，直线y＝x﹣12a与x轴交于点B，点M在抛物线上，且满足∠MAB＝75°的点M有且只有两个，求a的取值范围．

19．已知，如图1，抛物线与轴交于点、，与轴交于点，且，．

（1）求抛物线解析式；

（2）如图2，点是抛物线第一象限上一点，连接交轴于点，设点的横坐标为，线段长为，求与之间的函数关系式；

（3）在（2）的条件下，过点作直线轴，在上取一点（点在第二象限），连接，使，连接并延长交轴于点，过点作于点，连接、、．若时，求值．

20．如图，函数y＝﹣x2+bx+c的图象经过点A（m，0），B（0，n）两点，m，n分别是方程x2﹣2x﹣3＝0的两个实数根，且m＜n．

（Ⅰ）求m，n的值以及函数的解析式；

（Ⅱ）设抛物线y＝﹣x2+bx+c与x轴的另一个交点为C，抛物线的顶点为D，连接AB，BC，BD，CD．求证：△BCD∽△OBA；

（Ⅲ）对于（Ⅰ）中所求的函数y＝﹣x2+bx+c，

（1）当0≤x≤3时，求函数y的最大值和最小值；

（2）设函数y在t≤x≤t+1内的最大值为p，最小值为q，若p﹣q＝3，求t的值．