

备战2022年数学中考二次函数专项复习(word版含答案)
展开
备战2022数学中考二次函数专项复习
一、单选题
1.对于函数y= =ax2-(a+1)x+1,甲和乙分别得出一个结论:
甲:若该函数图象与x轴只有一个交点,则a=1;
乙:方程ax2- (a+1)x+1=0至少有一个整数根.
甲和乙所得结论的正确性应是( )
A.只有甲正确 B.只有乙正确
C.甲乙都正确 D.甲乙都不正确
2.将抛物线 y=x2−2x−1 向上平移1个单位,平移后所得抛物线的表达式是( )
A.y=x2−2x B.y=x2−2x−2
C.y=x2−x−1 D.y=x2−3x−1 .
3.拱桥的形状是抛物线,其函数关系式为y=−13x2,当水面离桥顶的高度为253m时,水面的宽度为( )米.
A.8 B.9 C.10 D.11
4.如图,一个矩形的长比宽多3cm,矩形的面积是Scm2.设矩形的宽为xcm,当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )
A.S=4x+6 B.S=4x-6 C.S=x2+3x D.S=x2-3x
5.已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法不正确的是( )
x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…
A.a<0
B.方程ax2+bx+c=﹣2的正根在4与5之间
C.2a+b>0
D.若点(5,y1)、(﹣32,y2)都在函数图象上,则y1<y2
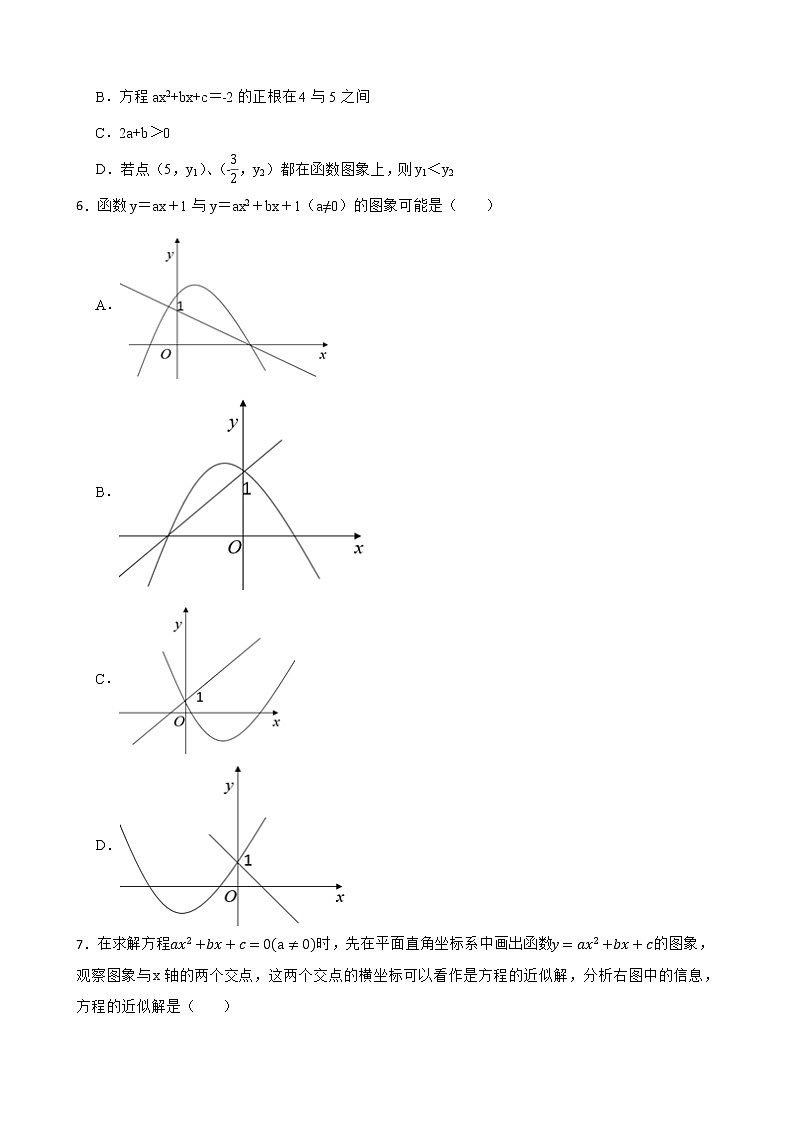
6.函数y=ax+1与y=ax2+bx+1(a≠0)的图象可能是( )
A.
B.
C.
D.
7.在求解方程ax2+bx+c=0(a≠0)时,先在平面直角坐标系中画出函数y=ax2+bx+c的图象,观察图象与x轴的两个交点,这两个交点的横坐标可以看作是方程的近似解,分析右图中的信息,方程的近似解是( )
A.x1=−3,x2=2 B.x1=−3,x2=3
C.x1=−2,x2=2 D.x1=−2,x2=3
8.新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y=x2−x+c(c为常数)在−2
A.3 B.23 C.3+2214 D.3+232
二、填空题
10.如果抛物线过点(−2,3),且与y轴的交点是(0,3),那么抛物线的对称轴是直线 .
11.据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为y万吨,如果2019年至2021年蔬菜产量的年平均增长率为x(x>0),那么y关于x的函数解析式为 .
12.若把函数y=x的图象用E(x,x)记,函数y=2x+1的图象用E(x,2x+1)记,……则E(x,x2−2x+3)图象上的最低点是 .
13.已知y是x的二次函数, y与x的部分对应值如下表:
x
...
-1
0
1
2
...
y
...
0
3
4
3
...
该二次函数图象向左平移 个单位,图象经过原点.
14.若点(m,0)在二次函数y=x2﹣3x+2的图象上,则2m2﹣6m+2029的值为 .
15.如图,二次函数y=ax2+bx+c的部分图象与y轴的交点为(0,3),它的对称轴为直线x=1,则下列结论中:①c=3;②2a+b=0;③8a-b+c>0;④方程ax2+bx+c=0的其中一个根在2,3之间,正确的有 (填序号).
三、解答题
16. 已知二次函数y=−316x2+bx+c的图象经过A(0,3),B(−4,−92)两点,求b,c的值.
17.现有一块直角三角形的材料, AB=80 cm, BC=60 cm,用它截下一个矩形,如图是截法示意图,求这种截法下矩形的最大面积是多少?
18.如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 t=−2x+80 ,求选取点B为坐标原点时的抛物线解析式.
19.“垃圾分类,利在千秋”.某废品回收站的废纸回收价为1.5元/千克,每天可回收100千克.回收价格每增加0.1元/千克,每天可多回收废纸40千克.如果废纸销往废品收购公司的价格为2.5元/千克,销售废纸的利润为 W 元,如何定回收价可以使得当天利润不低于150元?
20.抛物线 y=−12x2+bx+c 过点 A(−1,0) 和点 B(3,0) ,与 y 轴交于点 C ,顶点为点D.
(Ⅰ)求点 C,D 的坐标;
(Ⅱ)点 E 是线段 OB 上一动点,过点 E 作直线 l⊥x 轴,交抛物线于点 M ,连接 BM 并延长交 y 轴于点 N ,连接 AM,OM .若 △AEM 的面积是 △MON 面积的2倍,求点 E 的坐标;
(Ⅲ)抛物线上一点 T ,点 T 的横坐标是 −3 ,连接 BT ,与 y 轴交于点 P ,点 Q 是线段 AT 上一动点(不与点 A ,点 T 重合)将 △BPQ 沿 PQ 所在直线翻折,得到 △FPQ ,当 △FPQ 与 △TPQ 重叠部分的面积是 △TBQ 面积的 14 时,求线段 TQ 的长度.
21.如图,在平面直角坐标系中, O 为原点,抛物线 y=12x2+bx+c ( b , c 为常数),经过点 A(−4,0) 和点 B(0,−2) .
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点 P ,使 S△PAB=S△OAB ?若存在,请求出点 P 的坐标,若不存在,请说明理由;
(3)点 M 为直线 AB 下方抛物线上一点,点 N 为 y 轴上一点,当 △MAB 的面积最大时,直接写出 2MN+ON 的最小值.
答案解析部分
1.【答案】B
【解析】【解答】解:甲:当a=0时,y=-x+1,
∴当y=0时,x=1,即函数图象与x轴交于点(1,0),
∴甲结论不正确,
乙:当a=0时,-x+1=0,
∴x=1;
当a≠0时,ax2-(a+1)x+1=(x-1)(ax-1)=0,
解得x=1或x= 1a,
∴方程ax2-(a+1)x+1=0至少有一个整数根.
故答案为:B.
【分析】甲:当a=0时,函数y=-x+1,此时函数图象与x轴只有一个交点为(1,0),即可判断甲的结论;乙:当a=0时,-x+1=0,解得根为1,当a≠0时,ax2-(a+1)x+1=(x-1)(ax-1)=0,解得根为1或1a,据此即可判断乙结论.
2.【答案】A
【解析】【解答】解:∵将抛物线y=x2-2x-1向上平移1个单位,
∴平移后抛物线的表达式y=x2-2x-1+1,即y=x2-2x.
故答案为:A.
【分析】二次函数y=ax2+bx+c向上平移m(m>0)个单位长度,得到的新二次函数的解析式为y=ax2+bx+c+m.
3.【答案】C
【解析】【解答】解:根据题意,当y=−253时,−13x2=−253,解得:x=±5,
所以y=−13x2与y=−253的两个交点为(5,−253)和(-5,−253),
此时水面的宽度=5-(-5)=10米.
故答案为:C.
【分析】先求出x=±5,再求出交点坐标,最后求水面的宽度即可。
4.【答案】C
【解析】【解答】解:设矩形的宽为xcm,则长为(x+3)cm
由题意得:S=x(x+3)=x2+3x.
故答案为:C.
【分析】设矩形的宽为xcm,则长为(x+3)cm,根据矩形的面积公式可得S=x(x+3)=x2+3x.
5.【答案】B
【解析】【解答】解:∵二次函数值先由小变大,再由大变小,
∴抛物线的开口向下,
∴a<0,
故A不符合题意;
∵x=﹣1时,y=﹣3,
∴x=4时,y=﹣3,
∴二次函数y=ax2+bx+c的函数值为﹣2时,﹣1<x<0或3<x<4,
即方程ax2+bx+c=﹣2的负根在﹣1与0之间,正根在3与4之间,
故B符合题意;
∵抛物线过点(0,1)和(3,1),
∴抛物线的对称轴为直线x=32,
∴﹣b2a=32>1,
∴2a+b>0,
故C不符合题意;
∵(﹣32,y2)关于直线x=32的对称点为(92,y2),
∵92<5,
∴y1<y2,
故D不符合题意;
故答案为:B.
【分析】利用表中函数值的变化情况,可判断抛物线的开口方向,可对A进行判断;利用抛物线的对称性可得x的函数值相等,可对B进行判断;利用x的函数值相等可得抛物线的对称轴方程,可对C进行判断;利用二次函数的性质对D进行判断。
6.【答案】C
【解析】【解答】解:A、根据一次函数图象知道a<0,与y轴的交点不是(0,1),不符合题意;
B、根据二次函数的图象知道a<0,同时与y轴的交点是(0,1),但是根据一次函数的图象知道a>0,不符合题意;
C、根据图象知道两个函数图象与y轴的交点坐标为(0,1),同时也知道a>0,符合题意;
D、根据一次函数图象知道a<0,根据二次函数的图象知道a>0,不符合题意.
故答案为:C.
【分析】根据一次函数及二次函数与其系数的关系逐项判断即可。
7.【答案】D
【解析】【解答】解:因为两个交点的横坐标可以看作是方程的近似解,两个交点的横坐标为:x1=−2,x2=3,
所以方程的近似解是x1=−2,x2=3.
故答案为:D.
【分析】利用二次函数图像求一元二次方程的近似根即可。
8.【答案】B
【解析】【解答】解:由题意可得二倍点所在直线为y=2x,
将x=-2代入y=2x得y=-4,
将x=4代入y=2x得y=8,
设A(-2,-4),B(4,8),如图,
联立方程x2-x+c=2x,
当Δ>0时,抛物线与直线y=2x有两个交点,
即9-4c>0,
解得c<94,
此时,直线x=-2和直线x=4与抛物线交点在点A,B上方时,抛物线与线段AB有两个交点,
把x=-2代入y=x2-x+c得y=6+c,
把x=4代入y=x2-x+c得y=12+c,
∴6+c>−412+c>8,
解得c>-4,
∴-4<c<94满足题意.
故答案为:B.
【分析】设二倍点所在直线为y=2x,联立二次函数可得方程x2-x+c=2x,当Δ>0时,抛物线与直线y=2x有两个交点,求得c的取值范围,此时,直线x=-2和直线x=4与抛物线交点在点A,B上方时,抛物线与线段AB有两个交点;把x=-2代入y=x2-x+c得y=6+c,把x=4代入y=x2-x+c得y=12+c,则6+c>−412+c>8,解不等式组即可。
9.【答案】A
【解析】【解答】解:连接AO,AB,PB,作PH⊥OA于H,BC⊥AO于C,如图
当y=0时-x2+23x=0,得x1=0,x2=23,所以B(23,0),由于y=-x2+23x=-(x-3)2+3,所以A(3,3),所以AB=AO=23,AO=AB=OB,所以三角形AOB为等边三角形,∠OAP=30°得到PH= 12AP,因为AP垂直平分OB,所以PO=PB,所以OP+12AP=PB+PH,所以当H,P,B共线时,PB+PH最短,而BC=32AB=3,所以最小值为3.
故答案为:A.
【分析】连接AO、AB,PB,作PH⊥OA于H,BC⊥AO于C,如图,解方程得到B(23,0),利用配方法得到A(3,3),则OA=23,从而可判断三角形AOB为等边三角形,接着利用∠OAP=30°得到PH=12AP,利用抛物线的对称性得到PO=PB,所以OP+12AP=PB+PH,根据两点之间线段最短得到当H、P、B共线时,PB+PH的值最小,最小值为BC的长,然后计算出BC的长即可。
10.【答案】x=-1
【解析】【解答】解:∵当x=-2和x=0时,y的值都是3
∴该抛物线的对称轴是直线x=−2+02=−1
故答案为:x=−1.
【分析】根据点(−2,3)和点(0,3)的y值相等,即可得到两点关于对称轴对称,再利用对称轴的公式求解即可。
11.【答案】y=100(1+x)2(x>0)
【解析】【解答】解:根据题意可得:2020年的蔬菜产量为100(1+x),
2021年的蔬菜产量为100(1+x)(1+x)=100(1+x)2,
∴y=100(1+x)2(x>0),
故答案为:y=100(1+x)2(x>0) .
【分析】 2019年至2021年 ,2019年蔬菜产量为100万吨,即可得出答案。
12.【答案】(1,2)
【解析】【解答】解:根据题意得:该函数为y=x2−2x+3,
∵y=x2−2x+3=(x−1)2+2
∴当 x=1时,有最小值,最小值为 y=2,
即E(x, x2−2x+3)图象上的最低点是(1,2).
故答案为:(1,2).
【分析】根据题意得:该函数为y=x2-2x+3,将其化为顶点式,据此可得最低点的坐标.
13.【答案】3
【解析】【解答】解:由表格得:二次函数的对称轴是直线x=0+22=1.
∵抛物线与x轴的一个交点为(-1,0),
∴抛物线与x轴另一个交点为(3,0),
∴该二次函数图象向左平移3个单位,图象经过原点;或该二次函数图象向右平移1个单位,图象经过原点.
故答案为:3.
【分析】由表格可得:二次函数的对称轴是直线x= 0+22=1,根据对称性求出抛物线与x轴的另一个交点的坐标,接下来根据点的平移规律进行解答.
14.【答案】2025
【解析】【解答】解:∵ 点(m,0)在二次函数y=x2﹣3x+2的图象上,
∴m2−3m+2=0
即m2−3m=−2;
∴2m2﹣6m+2029=2(m2−3m)+2029=2×(−2)+2029=2025;
故应填2025.
【分析】将点(m,0)代入二次函数函数可得m2−3m+2=0,再将代数式 2m2﹣6m+2029变形为2(m2−3m)+2029,再计算即可。
15.【答案】①②④
【解析】【解答】解:∵二次函数y=ax2+bx+c的部分图象与y轴的交点为(0,3),
∴c=3,故①正确;
∵抛物线的对称轴为直线x=1,
∴ −b2a=1 ,即 2a+b=0 ,故②正确;
∵抛物线与x轴的一个交点在-1到0之间,抛物线对称轴为直线x=1,
∴抛物线与x轴的另一个交点在2到3之间,故④正确;
∵抛物线开口向下,
∴a<0,
∵当x=-1时, a−b+c<0 ,
∴ a−b+c+7a<0 即 8a−b+c<0 ,故③错误,
故答案为:①②④.
【分析】利用抛物线与y轴的交点可得到c的值,可对①作出判断;利用抛物线的对称轴,可得到2a+b=0,可对②作出判断;利用抛物线的对称性可知抛物线与x轴的另一个交点在2到3之间,可对④作出判断;观察函数图象可知当x=-1时y<0即a-b+c<0,由a<0,可知a-b+c+7a<0,可对③作出判断;综上所述可得到正确结论的序号.
16.【答案】解:把A(0,3) ,B(-4,-92) 分别代入y=−316x2+bx+c,
得c=3−316×16−4b+c=−92,
解得b=98c=3.
故b=98,c=3.
【解析】【分析】将点A、B的坐标代入求解就可得到b、c的值.
17.【答案】解:∵四边形BFED是矩形,
∴EF∥CB,
∴∠AEF=∠C ,
∵∠A=∠A ,
∴△AEF∽△ACB,
∴AFAB=EFCB ,
∵AB=80 cm, BC=60 cm,
设 BF=x ,则 AF=80−x ,
∴80−x80=EF60 ,
∴EF=60−34x ,
∴S=x(60−34x)=−34x2+60x=−34(x−40)2+1200 ( 0
∴这种截法下矩形的最大面积是1200 cm2.
【解析】【分析】先求出 △AEF∽△ACB, 再利用相似三角形的性质计算求解即可。
18.【答案】解:如图:
由题意可得出:y=a(x+6)2+4,
将(-12,0)代入得出,0=a(-12+6)2+4,
解得: a=−19 ,
∴选取点B为坐标原点时的抛物线解析式是: y=−19(x+6)2+4 .
故答案为: y=−19(x+6)2+4 .
【解析】【分析】先求出 0=a(-12+6)2+4, 再求出 a=−19 , 最后求解即可。
19.【答案】解:设回收价格增加 x 元/千克,则回收价为 (1.5+x) 元/千克,
根据题意可得:
W=[2.5−(1.5+x)](100+40×10x)
=(1−x)(100+400x)
=−400(x−38)2+6254 .
∵a=−400<0 ,
∴该二次函数的图象开口向下.
当 W=150 时,即 −400(x−38)2+6254=150 ,
解得: x1=14 , x2=12 ,
∴当 14≤x≤12 时, W≥150 ,
∴74≤1.5+x≤2 .
∴回收价大于等于 74 且小于等于2元/千克时,可以使得当天利润不低于150元.
【解析】【分析】设回收价格增加x元/千克,则回收价为(1.5+x)元/千克,每千克的利润为[2.5-(1.5+x)]元,每天回收的数量为(100+40×10x)千克,W=每千克的利润×销售数量建立出W关于x的二次函数,令W=150,解得相应的x值,根据二次函数的性质可得答案.
20.【答案】解:(Ⅰ)∵抛物线 y=−12x2+bx+c 经过点 A(−1,0) 和点 B(3,0) ,
得 −12−b+c=0−92+3b+c=0 ,解得 b=1c=32
∴抛物线的解析式为 y=−12x2+x+32 .
∵当 x=0 时, y=32 ,
∴点 C 的坐标为 (0,32) .
∵y=−12x2+x+32=−12(x−1)2+2 ,
∴顶点 D 的坐标为 (1,2) .
(Ⅱ)设点 E 的坐标为 (m,0),(0
∴点 M 的坐标为 (m,−12m2+m+32) .
设直线 BM 的解析式为 y=k1x+b1 ,
有 3k1+b1=0mk1+b1=−12m2+m+32. ,解得 k1=−12(m+1),b1=32(m+1).
∴直线 BM 的解析式为 y=−12(m+1)x+32(m+1) .
∵当 x=0 时, y=32(m+1) ,
∴点 N 的坐标为 (0,32(m+1)) .
S△AEM=12AE⋅ME=12(m+1)⋅(−12m2+m+32)=12(m+1)⋅(−12)(m+1)⋅(m−3) ,
S△MON=12ON⋅|xM|=12×32(m+1)⋅m ,
∵△AEM 的面积是 △MON 面积的2倍,
∴12(m+1)⋅(−12)(m+1)⋅(m−3)=2×12×32(m+1)⋅m
m2+4m−3=0,m=−2±7 ,
∵0
∴点 E 的坐标为 (−2+7,0) .
(Ⅲ)∵抛物线上一点 T ,点 T 的横坐标是 −3 ,
∴y=−12×(−3)2−3+32=−6 .
∴点 T 的坐标为 (−3,−6) .
设直线 BT 的解析式为 y=k2x+b2 ,
有 3k2+b2=0−3k2+b2=−6 ,解得 k2=1b2=−3
∴直线 BT 的解析式为 y=x−3 .
∵当 x=0 时, y=−3 .
∴点 P 的坐标为 (0,−3) .
过点 T 作 TG⊥y 轴于点 G ,则 TG=3, PG=3 ,
∴TP=TG2+PG2=32+32=32 .
又 BP=OB2+OP2=32+32=32 ,
∴BP=TP ,
∴点 P 是线段 BT 的中点.
∴S△BPQ=S△TPQ .
由折叠知, △BPQ≌△FPQ ,则 S△BPQ=S△FPQ .
∴S△FPQ=S△TPQ .
①如图,当点 F 在直线 BT 下方时,设线段 FQ 与线段 PT 交于点 M ,
△FPQ 与 △TPQ 重叠部分是 △MPQ ,连接 FT .
∵S△MPQ=14S△BTQ ,
∴S△MPQ=12S△TPQ=12S△FPQ .
∴MP=MT,MQ=MF .
∴四边形 FPQT 是平行四边形.
∴TQ=PF .
∵PF=BP,BP=32 ,
∴TQ=32 .
②如图,当点 F 在直线 BT 上方时,设线段 FP 与线段 QT 交于点 N,△FPQ 与 △TPQ 重叠部分是 △NPQ ,连接 FT .
同理可得,四边形 FTPQ 是平行四边形.
∴QF=TP=BP .
∵QF=BQ ,
∴BQ=BP=32 .
设直线 AT 的解析式为 y=k3x+b3 ,
有 −k3+b3=0−3k3+b3=−6 ,解得 k3=3b3=3
∴直线 AT 的解析式为 y=3x+3 .
设点 Q 的坐标为 (t,3t+3)(−3
BQ=EB2+EQ2=(t−3)2+(3t+3)2=32 ,解得 t1=0,t2=−65 .
∵−3
过点 Q 作 x 轴的平行线,过点 T 作 y 轴的平行线,两线交于点 H ,
∴TQ=QH2+TH2=(−65+3)2+(−35+6)2=9105 .
综上所述,线段 TQ 的长度为 32 或 9105 .
【解析】【分析】(Ⅰ)先求出抛物线的解析式为 y=−12x2+x+32,再求出 点 C 的坐标为 (0,32) ,最后求解即可;
(Ⅱ)先求出直线 BM 的解析式为 y=−12(m+1)x+32(m+1) ,再根据三角形的面积公式和函数图象求解即可;
(Ⅲ)先求出直线 BT 的解析式为 y=x−3 ,再分类讨论,计算求解即可。
21.【答案】(1)解:∵把点A(-4,0),点B(0,﹣2),
带入抛物线解析式为 y=12x2+bx+c
得 0=12×(−4)2+(−4b)+c−2=c , 解得 b=32c=−2
∴抛物线解析式为:y =12 x2+32 x﹣2;
(2)如图1,当点P在直线AB上方时,过点O作OP∥AB,交抛物线于点P,
∵OP∥AB,
∴△ABP和△ABO是等底等高的两个三角形,
∴S△PAB=S△ABO,
∵点 A(−4,0) 和点 B(0,−2) .
∴直线AB的解析式为 y=−12x−2
∵OP∥AB,
∴直线PO的解析式为y =−12 x,
联立方程组可得
解得: x=y= 或 x=y=
∴点P (−2+22,1−2) 或 (−2−22,1+2) ;
当点 P″ 在直线AB下方时,在OB的延长线上截取BE=OB=2,过点E作E P″ ∥AB,交抛物线于点 P″ ,连接A P″ ,B P″ ,
∴AB∥E P″ ∥OP,OB=BE,
∴S△AP″B =S△ABO,
∵E P″ ∥AB,且过点E(0,﹣4),
∴直线E P″ 解析式为y =12 x﹣4,
联立方程组可得 ,
解得 x=−2y=−3 ,
∴点 P″ (-2,﹣3),
综上所述:点P坐标为 (−2+22,1−2) 或 (−2−22,1+2) 或(-2,﹣3);
(3)如图2,过点M作MF⊥AC,交AB于F,
设点M(m, 12 m2+32 m﹣2),则点F(m,- 12 m﹣2),
∴MF =−12 m﹣2﹣( 12 m2+32 m﹣2) =−12 m2-2m,
∴△MAB的面积 =12× 4×( −12 m2-2m)= −m2−4m ,
∴当m=-2时,△MAB的面积有最大值,
∴点M(-2,﹣3),
如图3,过点O作∠KOB=30°,过点N作KN⊥OK于K点,过点M作MP⊥OK于P,延长MF交直线KO于Q,
∵∠KOB= 30° ,KN⊥OK,
∴KN =12 ON,
∴MN +12 ON=MN+KN,
∴当点M,点N,点K三点共线,且垂直于OK时,MN +12 ON有最小值,即最小值为MP,
∵∠KOB= 30° ,
∴直线OK解析式为y =3 x,
当x=2时,点Q(-2,2 3 ),
∴QM=2 3+ 3,
∵OB∥QM,
∴∠PQM=∠PON= 30° ,
∴PM =12 QM =3+32 ,
∴MN +12 ON的最小值为 3+32 ,即2MN + ON= 23+3 .
【解析】【分析】(1)利用待定系数法求函数解析式即可;
(2)先求出 S△PAB=S△ABO, 再求出直线E P″ 解析式为y =12 x﹣4,最后求解即可;
(3) 先求出 直线OK解析式为y =3 x, 再求出 PM =12 QM =3+32 , 最后计算求解即可。
备战中考数学《重难点解读•专项训练》专题03 二次函数与面积有关的问题(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题03 二次函数与面积有关的问题(专项训练),文件包含专题03二次函数与面积有关问题专项训练原卷版docx、专题03二次函数与面积有关问题专项训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
中考数学二轮专项复习——二次函数(压轴题专项)(含答案): 这是一份中考数学二轮专项复习——二次函数(压轴题专项)(含答案),共15页。
初中数学中考复习 备战2020年中考数学一轮复习——二次函数(压轴题专项)(含详细解析): 这是一份初中数学中考复习 备战2020年中考数学一轮复习——二次函数(压轴题专项)(含详细解析)












