人教版九年级上册第二十二章 二次函数综合与测试教学ppt课件

这是一份人教版九年级上册第二十二章 二次函数综合与测试教学ppt课件，共32页。PPT课件主要包含了函数图象共存问题，x0时yc，对称轴是y轴x0，简称左同右异，∴a-b+c-9a，∴-3b-6a，②④⑤⑦⑧，yk2x+b2等内容，欢迎下载使用。

抛物线与代数式值的正负性
根据已知条件确定函数图象
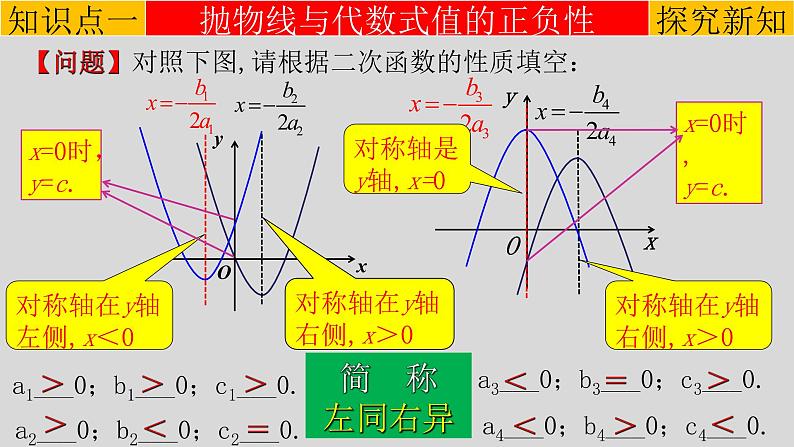
【问题】对照下图,请根据二次函数的性质填空：
a1___0；b1___0；c1___0.
a2___0；b2___0；c2___0.
对称轴在y轴左侧,x＜0
对称轴在y轴右侧,x＞0
a4___0；b4___0；c4___0.
a3___0；b3___0；c3___0.
【例1-1】跳绳能够让血液获得更多的氧气,能使心血管保持健康,还能改善脑部的血液循环,对于增强脑细胞的活力有很大好处,可以提高思维能力和想象能力.最近三年,跳绳作为我市体育中考项目得到大力推广和普及.如图,我们发现,在绳子运动到最高点时,绳子可以看做是二次函数y=ax2+bx+c(a≠0)的图象,下列选项中正确的是( ) A.a＞0 B.b＜0 C.c＞0 D.b2－4ac≥0
1.已知二次函数y=ax2+bx+c的图象如,下列结论：①abc＞0；②2a-b＜0；③4a-2b+c＜0；④a+c＜b.其中正确的个数是(　 ) A.1　 B.2　 C.3　 D.42.如图是抛物线y=ax2+bx+c(a≠0)的一部分,下列结论:①ab＜0；②b2-4ac＞0；③9a-3b+c＜0；④b-4a=0；⑤方程ax2+bx=0的两根为x1=0,x2=-4.其中正确的结论有( 　)A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
3.如图,二次函数y=ax2＋bx＋c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论：①2a＋b=0；②4a-2b＋c＞0；③abc＞0；④当y＜0时,x＜-1或x＞3.其中正确的是( )A.①② B.①③ C.①④ D.②③
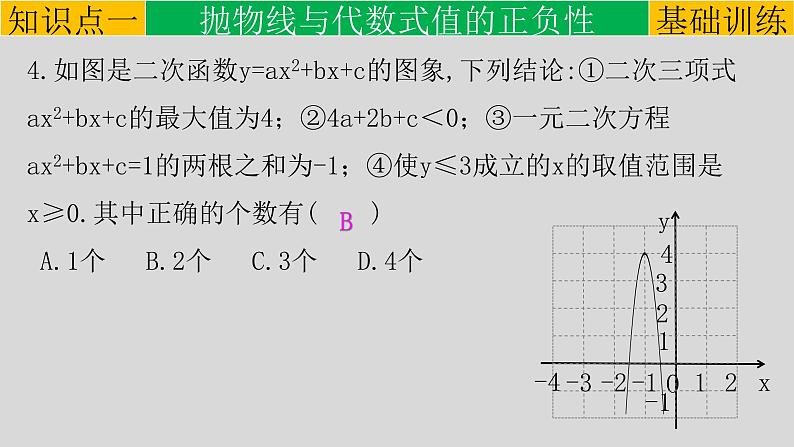
4.如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4；②4a+2b+c＜0；③一元二次方程ax2+bx+c=1的两根之和为-1；④使y≤3成立的x的取值范围是x≥0.其中正确的个数有(　　) A.1个 B.2个 C.3个 D.4个
5.如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4).则下列结论中错误的是(　　) A.若点(-2,m),(-5,n)在抛物线上,则m＞n B.关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 C.ax2+bx+c≥-6 D.b2＞4ac
1.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列判断:①b-2a=0,②4a-2b+c＜0,③a-b+c=-9a,④(-3,y1),(1.5,y2)是抛物线上两点,则y1＞y2.其中正确的是( ) A.①②③ B.①③④ C.①②④ D.②③④
③当x=-4时,y=16a-4b+c=0
∵-b/2a=-1得：b=2a,
∴10a-b+c=0,
2.二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论：①abc＞0；②a+b+c＞0；③a-b+c＜0；④2a+b=0；⑤4a+2b+c＞0；⑥3a+c＜0；⑦am2+bm＜a+b(m≠1)；⑧a+b≥m(am+b)(m为实数)。其中正确的有____________.
⑥∵a-b+c=0,b=-2a,∴3a+c=0
⑦⑧am2+bm+c≤a+b+c
3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论：①abc＜0；②b2-4ac＞0；③3a+c＞0；④(a+c)2＜b2,其中正确的结论有( )个 A.1 B.2 C.3 D.4
③∵a+b+c＜0,2a＜b,∴3a+c＜0④∵a+b+c＜0,a-b+c＞0,∴(a+b+c)(a-b+c)＜0∴(a+c)2＜b2
1.已知二次函数y=ax2+bx+c+2的图象如图.顶点为(-1,0),下列结论:①abc＜0；②b2-4ac=0；③a＞2；④4a-2b+c＞0.其中正确结论的个数是( 　) A.1 B.2 C.3 D.42.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论：①b2-4ac＞0；②abc＜0；③m＞2.其中正确结论的个数是( ) A.0 B.1 C.2 D.3
抛物线与代数式值的正负性
3.二次函数y=ax2+bx+c图象如图,下列结论错误的是( ) A.4ac＜b2 B.abc＜0 C.b+c＞3a D.a＜b
C.∵-b/2a＞-1, ∴-b＜-2a ∵a-b+c＞0 ∴a-2b+b+c＞0 ∴a-4a+b+c＞0 ∴b+c＞3aD.∵a-b+c＞0 ∴a-b＞-c＞0 ∴a＞b
4.如图,若抛物线y=ax2+bx+c(a≠0)经过点(-1,0),则下列结论①abc＞0；②a-b+c＝0；③2a+c＜0；④a+b＜0.其中正确的结论是( ) A.①③ B.②③ C.②④ D.②③④
③∵-b/2a＜0.5, ∴-b＞a ∵a-b+c＝0 ∴a+a+c＜0即2a+c＜0
5.二次函数y=ax2+bx+c(a≠0)的图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论：(1)8a+7b+2c＞0；(2)9a+c＞3b；(3)4a+b=0；(4)当x＞-1时,y的值随x值的增大而增大；(5)若点A(-3,y1),B(-0.5,y2),C(3.5,y3)在该函数图像上,则y1＜y3＜y2；(6)若方程a(x+1)(x-5)=-3的两根为x1,x2,且x1＜x2,则x1＜-1＜5＜x2。其中正确的结论有__________.
(1)∵b=-4a,a-b+c=0∴c=-5a ∴8a+7b+2c=-30a＜0
6.如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,OA=OC,对称轴为直线x=1,则下列结论：①abc＜0；② ③ac+b+1=0；④2+c是关于x的一元二次方程ax2+bx+c=0的一个根其中正确的有( )个 A.1 B.2 C.3 D.4
③把A(-c,0)代入y=ax2+bx+c得ac2-bc+c=0 ∴ac-b+1=0,∴③错误；④点B的坐标为(2+c,0)∴④正确。
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示：图象过点(-1,0)，对称轴为直线x=2,下列结论中不正确的是( ) A.4a+b=0 B.b2-4ac＞0 C.5a+c=0 D.若m≠2,则m(am+b)＞2(2a+b)
D.∵am2+bm+c≤4a+2b+c ∴am2+bm≤4a+2b ∴m(am+b)≤2(2a+b) ∴D错误
8.如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是B(1,3),与x轴的一个交点是A(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论：①abc＞0；②方程ax2+bx+c=3有两个相等的实数根；③抛物线与x轴的另一个交点是(-1,0)；④当1＜x＜4时,有y1＜y2；⑤x(ax+b)≤a+b.其中正确的结论是_____(只填写序号)
9.二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论:①c＜0；②b＞0；③4a+2b+c＞0；④(a+c)2＜b2.其中不正确的有( )个 A.1 B.2 C.3 D.4
④∵a+b+c＜0,a-b+c＜0 ∴(a+b+c)(a-b+c)＞0 ∴(a+c)2-b2＞0 ∴(a+c)2＞b2故④错误
【问题】一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空：
k1___0b1___0
k3 ___0b3 ___0
k4 ___0b4 ___0
k2___0b2___0
【例2】在同一直角坐标系中，一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
1.两个函数中相同的字母系数一定要符号相同；2.两个函数中不同的字母系数一般不用考虑；3.数字系数一定要注意。
2.在同一直角坐标系中,一次函数y=ax+b与二次函数y=bx2+a的图象可能是( )
1.在同一直角坐标系中,一次函数y=ax+b和二次函数y=ax2+b的图象可能为(　　)
3.当ab＞0时,y=ax2与y=ax+b的图象大致是( )
4.在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
5.函数y=ax+b(a≠0)和y=ax2+bx+c(a≠0)在同一平面直角坐标系内的图象可能是( )
6.如图,函数y=ax2-2x+1和y=ax+a(a≠0)在同一平面直角坐标系的图象可能是( )
1.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
2.二次函数y=ax2+bx+c与y=bx2+ax+c的图象可能是( )
3.已知a,b是非零的实数,│a│＞│b│,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的图象不可能是( )
由ax2+bx=ax+b∴x1=1,x2=-b/a得交点为(1,a+b)(-b/a,0)
【例3】已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是(　　)
1.若二次函数y=a(x+m)2+n的图像如图,则一次函数y=mx+n的图像经过第____________象限。