备考2022中考数学一轮专题复习学案05 二次根式

这是一份备考2022中考数学一轮专题复习学案05 二次根式，共7页。

中考命题说明
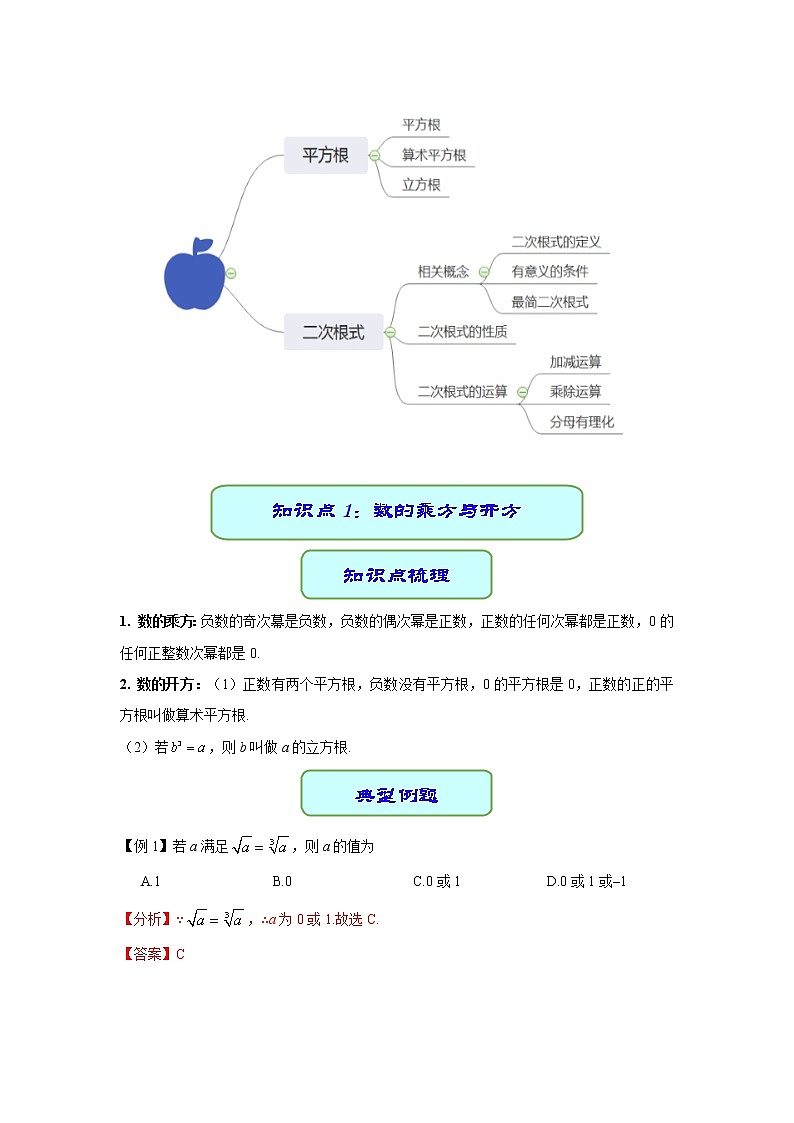
思维导图
知识点1：数的乘方与开方
知识点梳理
1. 数的乘方：负数的奇次幕是负数，负数的偶次幂是正数，正数的任何次幂都是正数，0的任何正整数次幂都是0.
2. 数的开方：（1）正数有两个平方根，负数没有平方根，0的平方根是0，正数的正的平方根叫做算术平方根.
（2）若，则b叫做a的立方根.
典型例题
【例1】若a满足，则a的值为
A.1B.0C.0或1D.0或1或–1
【分析】∵，∴a为0或1.故选C.
【答案】C
知识点2：二次根式的概念和性质
知识点梳理
1.二次根式：形如(a≥0)的式子叫做二次根式.
2.二次根式有意义的条件：被开方数大于或等于 0 .
3.最简二次根式：必须同时满足以下两个条件：
(1)被开方数不含分母；
(2)被开方数中不含能开得尽方的因数或因式.
如： QUOTE ， QUOTE 是最简二次根式，而，， QUOTE 都不是最简二次根式.
4.同类二次根式：当二次根式化为最简二次根式后，如果被开方数相同，那么这几个二次根式叫做同类二次根式.
5.二次根式的性质：
(1)()2= a (a≥0).
(2)=|a|= QUOTE
(3) (a ≥ 0，b ≥ 0).
(4) (a ≥ 0，b > 0).
典型例题
【例2】若 QUOTE 有意义，则x的取值范围是( )
A.x≥2B.x≥-2 C.x>2D.x>-2
【分析】本题考查二次根式有意义的条件，根据被开方数大于或等于0，列出不等式x-2≥0，解不等式即可.
【答案】A.
知识点3：非负性
知识点梳理
1.概念：正数和零叫做非负数.常见的非负数有|a|，a2，(a≥0).
2.性质：若几个非负数的和等于零，则这几个数都为零.
如：若a2+|b|+=0，则a2=0，|b|=0，=0，可得a=b=c=0.
典型例题
【例3】已知|a-1|+ QUOTE =0，则ab= .
【分析】∵|a-1|+ QUOTE =0，则|a-1|=0， QUOTE =0，解得：a=1，b=-2.∴ab=1-2=1.故答案为：1.
【答案】1.
【例4】单项式x-|a-1|y与2 QUOTE y是同类项，则ab= .
【分析】由题意知-|a-1|= QUOTE ，
∴a=1，b=1，则ab=11=1.
故答案为：1.
【答案】1.
知识点4：二次根式的化简与运算
知识点梳理
1.加减运算：先将二次根式化为最简二次根式，再将被开方数相同的二次根式进行合并.
2.乘除运算：
(a ≥ 0，b ≥ 0)；
QUOTE (a ≥ 0，b > 0).
3.混合运算：与实数的运算顺序相同.运算结果必须为最简二次根式.
4.把分母中的根号化去（分母有理化）的方法：
(1)；
(2).
典型例题
【例5】下列计算：(1)( QUOTE )2=2，(2) QUOTE =2，(3)()2=12，(4)()()=-1，其中结果正确的个数为( )
A.1B.2C.3D.4
【分析】（1）( QUOTE )2=2，正确；（2） QUOTE = QUOTE =2，正确；（3）()2=4×3=12，正确；（4）()()=()2-()2=2-3=-1，正确.故（1）（2）（3）（4）都正确，故答案为：D.
【答案】D.
【例6】计算：= .
【分析】原式=
=2(+1)-(2+2+1)
=2+2-2-2-1
=-1.
【答案】-1.
知识点5：二次根式的估值
知识点梳理
一般步骤：
1.一般先对根式进行平方，如()2=5；
2.找出与平方后所得数相邻的两个完全平方数，如4