初中数学北师大版八年级下册1 等腰三角形教学演示ppt课件

这是一份初中数学北师大版八年级下册1 等腰三角形教学演示ppt课件，共11页。PPT课件主要包含了基本事实，同位角，两边及其夹角，两角及其夹边，用心想一想马到功成，议一议做一做，一题多解，证法一，等腰三角形的性质，证法二等内容，欢迎下载使用。
1.两直线被第三条直线所截,如果________相等,那么这两条直线平行; 2.两条平行线被第三条直线所截,________相等; 3. ____________对应相等的两个三角形全等; （SAS）4. ____________对应相等的两个三角形全等; （ASA）5. _____对应相等的两个三角形全等; （SSS） 你能证明下面的推论吗？推论　两角及其中一角的对边对应相等的两个三角形全等.（AAS）
耐心填一填，一锤定音！
推论　两角及其中一角的对边对应相等的两个三角形全等.（AAS）
已知：如图,∠A=∠D,∠B=∠E,BC=EF.求证：△ABC≌△DEF.
证明：∵∠A+∠B+∠C=180°， ∠D+∠E+∠F=180°（三角形内角和等于180°） ∴∠C=180°－(∠A+∠B)，∠F=180°－(∠D+∠E) ∵∠A=∠D,∠B=∠E（已知） ∴∠C=∠F（等量代换） ∵BC=EF（已知） ∴△ABC≌△DEF（ASA）
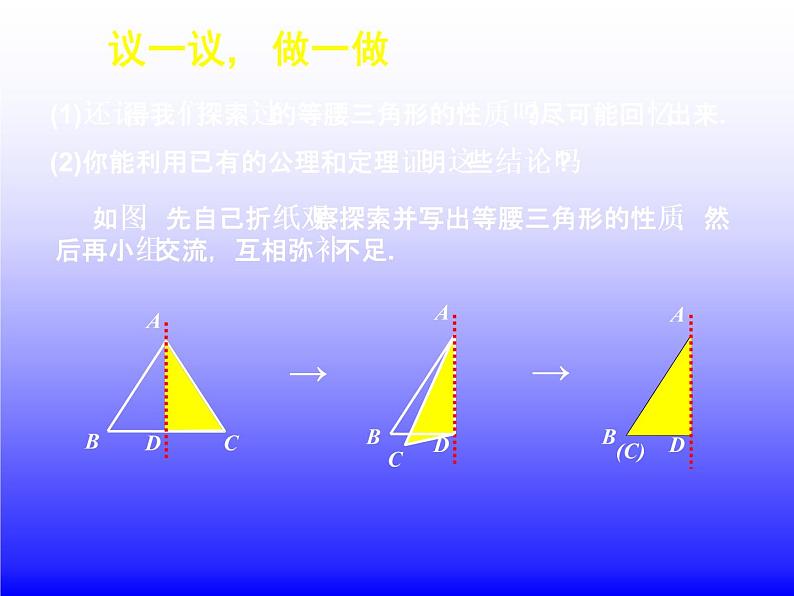
(1)还记得我们探索过的等腰三角形的性质吗?尽可能回忆出来.(2)你能利用已有的公理和定理证明这些结论吗?
如图，先自己折纸观察探索并写出等腰三角形的性质，然后再小组交流，互相弥补不足.
定理: 等腰三角形的两个底角相等. (等边对等角)
已知：如图, 在△ABC中, AB=AC.求证：∠B=∠C.
证明：取BC的中点D, 连接AD. 在△ABD和△ACD中 ∵ AB=AC, BD=CD, AD=AD ∴ △ABD≌△ACD (SSS) ∴ ∠B=∠C （全等三角形的对应角相等）
证明：作△ABC顶角∠A的角平分线AD. 在△ABD和△ACD中 ∵ AB=AC, ∠BAD=∠CAD, AD=AD ∴ △ABD≌△ACD (SAS) ∴ ∠B=∠C （全等三角形的对应角相等）
证明：在△ABC和△ACB中 ∵ AB=AC, ∠A=∠A, AC=AB, ∴ △ABC≌△ACB (SAS) ∴ ∠B=∠C （全等三角形的对应角相等）
点拨：此题还有多种证法，不论怎样证，依据都是全等的基本性质。
在上面的图形中,线段AD还具有怎样的性质?为什么?由此你能得到什么结论?
推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. (三线合一)
1.等腰三角形的两个底角相等； 2.等腰三角形顶角的平分线、底边中线、底边上高三条线重合；
2. 如图,在△ABD中,C是BD上的一点，且AC⊥BD，AC=BC=CD，（1）求证： △ABD是等腰三角形;（2）求∠BAD的度数.