专练12 期末模拟测试（1）-2021-2022学年八年级数学下学期期末考点必杀200题（人教版，广东专用）

这是一份专练12 期末模拟测试（1）-2021-2022学年八年级数学下学期期末考点必杀200题（人教版，广东专用），文件包含专练12期末模拟测试1解析版-2021-2022学年八年级数学下学期期末考点必杀200题人教版广东专用docx、专练12期末模拟测试1原卷版-2021-2022学年八年级数学下学期期末考点必杀200题人教版广东专用docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
专练12 期末模拟测试（1） （解析版）
2021-2022学年八年级数学下学期期末考点必杀200题
（人教版，广东专用）
姓名：___________班级：___________考号：___________

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）
1．下列各式中，是最简二次根式的是（ ）
A． B． C． D．
【答案】C
【分析】
利用最简二次根式定义判断即可．
【详解】
解：A、，不是最简二次根式；
B、，不是最简二次根式；
C、是最简二次根式；
D、，不是最简二次根式；
故选C．
【点睛】
此题考查了最简二次根式，熟练掌握最简二次根式定义是解本题的关键．
2．下列各组数中，是勾股数的是（ ）
A． B． C． D．
【答案】B
【分析】
根据勾股数的定义：三边是正整数且两小边的平方和等于第三边的平方，进行求解即可．
【详解】
根据勾股数的定义可得，
，
故选：B．
【点睛】
本题考查了勾股数，熟练勾股数的定义是解决本题的关键．
3．若点P（1，6）关于y轴的对称点在一次函数y＝（3k＋2）x－1的图象上，则k的值为（ ）
A．－1 B．1 C．3 D．－3
【答案】D
【分析】
根据P的坐标可得它关于y轴对称点的坐标（-1，6），再把（-1，6）代入关系式可得k的值．
【详解】
解：P（1，6）关于y轴的对称点是（-1，6），
把（-1，6）代入可得：，
解得：．
故选：D．
【点睛】
本题考查了一次函数的性质、关于y轴对称的点的坐标，解答本题的关键是明确题意，利用一次函数的性质解答．
4．下列各式中，正确的是（ ）
A． B． C． D．
【答案】C
【分析】
A、原式合并同类二次根式得到结果，即可做出判断；B、原式化为最简二次根式，即可做出判断；C、原式利用二次根式性质计算得到结果，即可做出判断；D、原式利用二次根式性质计算得到结果，即可做出判断．
【详解】
解：A、原式=，故错误；
B、原式=，故错误；
C、原式=5，故正确；
D、原式=|-5|=5，故错误，
故选：C．
【点睛】
此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
5．某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：
尺码
39
40
41
42
43
平均每天销售数量（件）
10
12
12
20
12
该店主决定本周进货时，增加了一些42码的衬衫，影响该店主决策的统计量是（ ）．
A．众数 B．方差 C．平均数 D．中位数
【答案】A
【分析】
根据众数的意义，即可得到答案．
【详解】
根据表格数据，可得：42码是众数，
故增加了一些42码的衬衫，影响该店主决策的统计量是众数，
故选A．
【点睛】
本题主要考查根据合适的统计量作决策，理解众数的意义，是解题的关键．
6．（2020·深圳市福田区外国语学校八年级期中）在下列命题中，结论正确的是（ ）
A．对角相等的四边形是平行四边形
B．一组对边平行另一组对边相等的四边形是平行四边形
C．平行四边形的两条对角线长度相等
D．平行四边形的邻角相等
【答案】A
【分析】
根据平行四边形的判定方法分别对各个选项进行判断即可．
【详解】
解：A、由平行四边形的判定可知，对角相等的四边形是平行四边形，A选项说法正确，符合题意．
B、根据等腰梯形的定义可以判定B选项说法不正确，不符合题意．
C、平行四边形的对角线不一定相等，C选项说法不正确不符合题意．
D、由平行四边形的定义可知，平行四边形的邻角互补，邻角相等的平行四边形是矩形，但是平行四边形的邻角不一定相等，此选项说法不正确，不符合题意．
故选A．
【点睛】
本题考查了平行四边形的判定；熟练掌握平行四边形的判定方法是解题的关键．
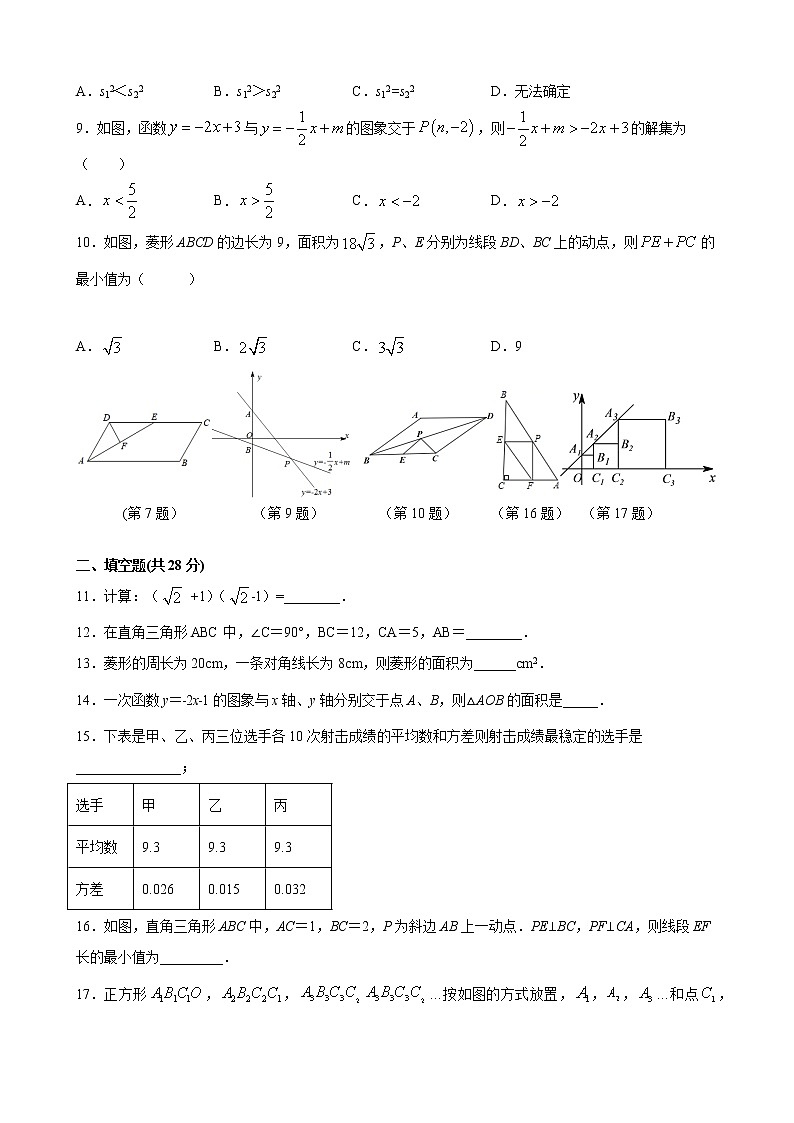
7．如图，在▱ABCD中，AB=4，∠BAD的平分线交DC于点E，且点E恰好是DC的中点，过点D作DF⊥AE，垂足为F．若AE=，则DF的长为（ ）

A． B． C．1 D．
【答案】C
【分析】
由等腰三角形的性质可求AF=EF=，由勾股定理可求解．
【详解】
解：∵AB=4，点E是DC的中点，
∴DE=EC=2，
∵AE为∠DAB的平分线，
∴∠DAE=∠BAE，
∵DC∥AB，
∴∠BAE=∠DEA，
∴∠DAE=∠DEA，
∴AD=ED=2，
∵DF⊥AE，
∴AF=EF=AE=，
∴DF==1，
故选：C．
【点睛】
本题考查了平行四边形的性质，等腰三角形的判定和性质，勾股定理，掌握平行四边形的性质是本题的关键．
8．小亮要计算一组数据80，82，74，86，79的方差s12，在计算平均数的过程中，将这组数据中的每一个数都减去80，得到一组新数据0，2，－6，6，－1，记这组新数据的方差为s22，则s12与s22的大小关系为（ ）
A．s12＜s22 B．s12＞s22 C．s12=s22 D．无法确定
【答案】C
【分析】
分别求两组数据的平均数，再求两组数据的方差进行比较即可．
【详解】
解：，
s12=，
=，
，
s22=，
=，
∴s12=s22．
故选择：C．
【点睛】
本题考查平均数，方差，掌握平均数，方差，特别是构造新数组，不影响方差，当遇到数组中数据较大时，可以构造新数组解决问题是关键．
9．如图，函数与的图象交于，则的解集为（ ）

A． B． C． D．
【答案】B
【分析】
先把P（n，-2）代入y=-2x+3求出n得到P的坐标，根据图象直接写出直线y=- x+m在直线y=-2x+3的上方所对应的自变量的范围即可．
【详解】
解：把P（n，-2）代入y=-2x+3得-2n+3=-2，解得n=；
∴P（，-2），
观察图象，当x＞时，直线y=- x+m在直线y=-2x+3的上方，
∴不等式-x+m＞-2x+3的解集为x＞．
故选：B．
【点睛】
本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
10．如图，菱形ABCD的边长为9，面积为，P、E分别为线段BD、BC上的动点，则的最小值为（　　　）

A． B． C． D．9
【答案】B
【分析】
过作于 交于由菱形在轴对称性质可得： 可得 此时最短，再利用菱形的面积公式可得答案．
【详解】
解：过作于 交于

由菱形在轴对称性质可得：

此时最短，
菱形ABCD的边长为9，面积为，



所以的最小值是
故选：
【点睛】
本题考查的是勾股定理的应用，菱形的性质，利用轴对称求解线段和的最小值，掌握以上知识是解题的关键．


二、填空题(共28分)
11．（2020·深圳市高级中学八年级期中）计算：（ +1）（﹣1）=________．
【答案】1
【分析】
利用平方差公式进行计算即可．
【详解】
解：（ +1）（﹣1）
=（）2﹣12
=2﹣1
=1，
故答案为：1．
【点睛】
本题考查了二次根式的乘法、平方差公式，熟记平方差公式是解答的关键．
12．（2020·和平县实验初级中学）在直角三角形ABC中，∠C＝90°，BC＝12，CA＝5，AB＝________．
【答案】13．
【分析】
直接根据勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方进行计算即可．
【详解】
解：根据勾股定理可得AB==13，
故答案为：13．
【点睛】
本题主要考查了勾股定理：如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．掌握勾股定理的内容是解题的关键．
13．（2020·广东惠州市·八年级期中）菱形的周长为20cm，一条对角线长为8cm，则菱形的面积为______cm2．
【答案】24
【分析】
画出符合题意的图形，利用菱形的对角线互相垂直平分，求解另一条对角线的长，再利用菱形的面积等于两条对角线的长之积的一半即可得到答案．
【详解】
解：如图，菱形的周长为20cm，一条对角线的长为8cm，





故答案为：
【点睛】
本题考查的是菱形的性质，菱形的面积，掌握菱形的性质及菱形的面积的计算是解题的关键．
14．（2021·广东茂名市·八年级期末）一次函数y＝﹣2x﹣1的图象与x轴、y轴分别交于点A、B，则△AOB的面积是_____．
【答案】
【分析】
先求出一次函数图像与坐标轴的交点坐标，再利用三角形的面积公式，即可求解．
【详解】
解：当x＝0时，y＝﹣2×0﹣1＝﹣1，
∴点B的坐标为（0，﹣1），
∴OB＝1；
当y＝0时，﹣2x﹣1＝0，解得：x＝﹣，
∴点A的坐标为（﹣，0），
∴OA＝．
∴S△AOB＝OA•OB＝．
故答案为：．
【点睛】
本题主要考查一次函数与平面几何综合，掌握一次函数图像与坐标轴的交点坐标求法，是解题的关键．
15．（2020·广东肇庆市·八年级期末）下表是甲、乙、丙三位选手各10次射击成绩的平均数和方差则射击成绩最稳定的选手是_______________；
选手
甲
乙
丙
平均数
9.3
9.3
9.3
方差
0.026
0.015
0.032

【答案】乙
【分析】
从统计表可以看出甲、乙、丙三位选手的平均数相同，进一步比较方差，方差小的数据的比较稳定，由此解决问题即可．
【详解】
解：因为0.015＜0.026＜0.032，
即乙的方差＜甲的方差＜丙的方差，
因此射击成绩最稳定的选手是乙．
故答案为：乙．
【点睛】
此题主要利用方差来判定数据的波动性，方差越小，数据越稳定．
16．（2019·广东实验中学附属天河学校）如图，直角三角形ABC中，AC＝1，BC＝2，P为斜边AB上一动点．PE⊥BC，PF⊥CA，则线段EF长的最小值为_________．

【答案】．
【分析】
先连接PC，判定四边形ECFP是矩形，得到EF=PC，再根据当PC最小时，EF也最小，根据垂线段最短，可得当CP⊥AB时，PC最小，最后根据面积法，求得CP的长即可得到线段EF长的最小值．
【详解】
解：连接PC，

∵PE⊥BC，PF⊥CA，
∴∠PEC=∠PFC=∠C=90°，
∴四边形ECFP是矩形，
∴EF=PC，
∴当PC最小时，EF也最小，
∵垂线段最短，
∴当CP⊥AB时，PC最小，
∵AC=1，BC=2，
∴AB=，
又∵当CP⊥AB时，×AC×BC=×AB×CP，
∴．
∴线段EF长的最小值为．
故答案为：．
【点睛】
本题主要考查了矩形的判定与性质，勾股定理以及垂线段最短的综合应用，解决问题的关键是运用矩形对角线相等的性质进行求解．
17．（2020·佛山市顺德区北滘镇碧江中学八年级月考）正方形，，…按如图的方式放置，，，…和点，，…分别在直线和轴上，则点的横坐标是_________

【答案】14
【分析】
先利用直线的解析式可求出点的坐标，从而可得的长，再利用直线的解析式分别求出的坐标，然后利用正方形的性质即可得．
【详解】
对于直线，
当时，，即，
，
四边形，，都是正方形，
，
点的横坐标为2，
将代入直线解析式得：，即，
，
，
点的横坐标为6，
将代入直线解析式得：，即，
，
，
则点的横坐标为14，
故答案为：14．
【点睛】
本题考查了正方形的性质、一次函数图象上的点坐标等知识点，熟练掌握一次函数的性质是解题关键．

三、解答题(共62分)
18．(本题6分)（2021·福建厦门市·厦门双十中学八年级月考）（1）
（2）
【答案】（1）；（2）4
【分析】
（1）根据平方差公式展开，再根据二次根式性质计算即可；
（2）利用乘法分配律展开计算即可；
【详解】
原式，
；
原式，
，
；
【点睛】
本题主要考查了二次根式的混合运算，结合平方差公式计算是解题的关键．
19．(本题6分)（2020·广东清远市·）如图，在平面直角坐标系中，Rt△ABC的三个顶点坐标为A（﹣3，0），B（﹣3，﹣3），C（﹣1，﹣3）．
（1）在图中作出△ABC关于x轴对称的图形△DEF；
（2）求线段DF的长．

【答案】（1）见解析；（2）
【分析】
（1）分别作出点B与点C关于x轴的对称点，再与点A首尾顺次连接即可得．
（2）利用勾股定理进行计算可得线段DF的长．
【详解】
解：（1）如图所示，△DEF即为所求；

（2）由勾股定理得，线段DF的长为＝．
【点睛】
本题考查作图-轴对称变换，解题关键是熟练掌握轴对称变换的定义和性质．
20．(本题6分)（2021·广东佛山市·八年级期末）为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测试，两个人在相同条件下各射靶5次，甲命中的环数分别是：10、6、10、6、8，乙命中的环数分别是：7、9、7、8、9.经过计算，甲命中的平均数为，方差为．
（1）求乙命中的平均数和方差；
（2）现从甲、乙两名队员中选出一人去参加射击比赛，你认为应该选哪名队员去？为什么？
【答案】（1）；；（2）乙，见解析
【分析】
（1）利用平均数以及方差的定义得出即可；
（2）利用方差的意义，分析得出答案即可．
【详解】
解：（1）（个），
；
（2）应选乙去，
理由：∵
∵，，
∴，
∴乙的波动小，成绩更稳定
∴应选乙去参加射击比赛．
【点睛】
此题主要考查了平均数以及方差，正确记忆相关定义是解题关键．
21．(本题6分)（2021·陕西西安市·西安工业大学附中九年级其他模拟）在中，对角线平分交于点，交于点．


（1）求证：；
（2）若，求的长．
【答案】（1）见解析；（2）．
【分析】
（1）根据平行四边形的性质可得再由平行线的性质可得，由角平分线的定义可得，即可得，由此可得；
（2）由勾股定理求得，过点F作于点H，根据角平分线的性质定理可得AF=FH，再由，即可得，由此即可求得．
【详解】
（1）∵四边形ABCD为平行四边形，
∴，
∴
∵平分，
∴，
∴，
∴；
（2）∵，，
∴，
过点F作于点H，


∵平分，，
∴AF=FH，
∵，
∴，
即，
∴．
【点睛】
本题考查了平行四边形的性质、等腰三角形的判定、角平分线的性质定理，熟练运用相关性质及定理是解决问题的关键．
22．(本题6分)（2020·佛山市顺德区北滘镇碧江中学八年级月考）如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量（千瓦时）关于已行驶路程（千米）的函数图象.

（1）根据图象，蓄电池剩余电量为50千瓦时时汽车已经行驶的路程为 千米，当时，消耗1千瓦时的电量，汽车能行驶的路程为 千米；
（2）当蓄电池的剩余电量10千瓦时的时候电动汽车需再次充电，计算这时汽车行驶路程．
【答案】（1）200，；（2）300千米．
【分析】
（1）根据函数图象即可得，再根据行驶200千米，消耗30千瓦时的电量即可得；
（2）先利用待定系数法求出时，y与x的函数关系式，再求出时，x的值即可得．
【详解】
（1）由函数图象可知，蓄电池剩余电量为50千瓦时时汽车已经行驶的路程为200千米，
由图象得：，
则当时，消耗1千瓦时的电量，汽车能行驶的路程为千米，
故答案为：200，；
（2）当时，设y与x的函数关系式，
将点和代入得：，
解得，
则当时，设y与x的函数关系式，
因此，当时，，解得，
故这时汽车行驶路程为300千米．
【点睛】
本题考查了从函数图象获取信息、利用待定系数法求一次函数的解析式，读懂函数图象，熟练掌握待定系数法是解题关键．
23．(本题6分)（2021·广东深圳市·深圳外国语学校八年级期末）某校在八年级开展环保知识问卷调查活动，问卷一共10道题，每题10分，八年级（三）班的问卷得分情况统计图如下图所示：

（1）扇形统计图中，a的值为 ________．
（2）根据以上统计图中的信息，求这问卷得分的众数和中位数分别是多少分？
（3）已知该校八年级共有学生600人，请估计问卷得分在80分以上（含80分）的学生约有多少人？
【答案】（1）；（2）90分，85分；（3）420
【分析】
（1）利用60分的百分比a等于1减去其他部分的百分比即可得到；
（2）先计算得出调查的总人数，找到这组数据从低到高排列的第25、26个得分，即可即可得到中位数；
（3）用600乘以80分及以上的百分比即可得到答案.
【详解】
（1）；
（2）①问卷得分的众数是90分，
②问卷调查的总人数为： （人），
第25、26个人的得分分别为80分、90分，
问卷得分的中位数是（分）；
（3）（人）
答：估计问卷得分在80分以上（含80分）的学生约有420人.
【点睛】
此题考查数据的整理计算，能正确计算部分的百分比，求数据的总数，中位数，利用样本的数据计算总体的对应数据.
24．(本题8分)（2020·珠海市第八中学八年级期中）一架云梯长13m，如图所示斜靠在一面墙上，梯子底端C离墙5m．
（1）这个梯子AC的顶端A距地面有多高？
（2）如果梯子的顶端下滑了3m，如图到达DE位置，那么梯子的底部在水平方向滑动的距离CE是多少米？

【答案】（1）梯子的高为12 m；（2）(-5)m
【分析】
（1）直接根据勾股定理求出AB的长即可；
（2）先根据梯子的顶端下滑了3米求出AD的长，再根据勾股定理求出BE的长，进而可得出结论．
【详解】
解：（1）由题意可知△ABC是直角三角形，
∵BC＝5m AC＝13m．
∴由勾股定理得：AB＝＝12（m），
∴梯子的高为12 m；
（2）由题意可知DE＝AC＝13m，
∵AD＝3m，
∴BD＝12﹣3＝9（m），
在Rt△DBE中，由勾股定理得：BE＝＝＝2（m），
∴﹣5）（m）．
【点睛】
本题考查了勾股定理的应用，勾股定理揭示了直角三角形三边长之间的数量关系：直角三角形两直角边的平方和等于斜边的平方．当题目中出现直角三角形，且该直角三角形的一边为待求量时，常使用勾股定理进行求解这在几何的计算问题中是经常用到的，请同学们熟记并且能熟练地运用它．
25．(本题8分)（2021·重庆九年级其他模拟）已知：如图，一次函数y1＝﹣x﹣2与y2＝x﹣4的图象相交于点A．
（1）求点A的坐标．
（2）若一次函数y1与y2的图象与x轴分别相交于点B、C，求△ABC的面积．
（3）结合图象，直接写出y1≤y2时x的取值范围．

【答案】（1）；（2）9；（3）
【分析】
（1）联立两个函数解析式，解方程组可求点的坐标；
（2）分别求出、两点坐标，然后可得的面积；
（3）根据图象可直接得到时的取值范围．
【详解】
解：（1）联立两函数解析式可得方程组，
解得：，
点的坐标为；
（2）当时，，解得：，
，
当时，，解得：，
，
，
的面积为：；
（3）由图象可得：时的取值范围是．
【点睛】
此题主要考查了一次函数和一元一次不等式，二元一次方程组，关键是正确求出两函数图象与轴交点，掌握数形结合思想．
26．(本题10分)（2020·广东广州市·执信中学八年级期中）如图，两个正方形ABCD与DEFG，连结AG，CE，二者相交于点H．
（1）证明：△ADG≌△CDE；
（2）请说明AG和CE的位置和数量关系，并给予证明；
（3）连结AE和CG，请问△ADE的面积和△CDG的面积有怎样的数量关系？并说明理由．

【答案】(1)答案见解析；(2) AG=CE，AG⊥CE；(3) △ADE的面积=△CDG的面积
【分析】
（1）利用SAS证明△ADG≌△CDE；
（2）利用△ADG≌△CDE得到AG=CE，∠DAG=∠DCE，利用∠DAG+∠AMD=90°得到∠DCE+∠CMG=90°，即可推出AG⊥CE；
（3）△ADE的面积=△CDG的面积，作GP⊥CD于P，EN⊥AD交AD的延长线于N，证明 △DPG≌△DNE，得到PG=EN，再利用三角形的面积公式分别表示出△ADE的面积，△CDG的面积，即可得到结论△ADE的面积=△CDG的面积.
【详解】
（1）∵四边形ABCD与DEFG都是正方形，
∴AD=CD，DG=DE，∠ADC=∠EDG=90°，
∴∠ADC+∠CDG=∠EDG+∠CDG，
∴∠ADG=∠CDE，
∴△ADG≌△CDE（SAS），
（2）AG=CE，AG⊥CE，
∵△ADG≌△CDE，
∴AG=CE，∠DAG=∠DCE，
∵∠DAG+∠AMD=90°，∠AMD=∠CMG，
∴∠DCE+∠CMG=90°，
∴∠CHA=90°，
∴AG⊥CE；

（3）△ADE的面积=△CDG的面积，
作GP⊥CD于P，EN⊥AD交AD的延长线于N，则∠DPG=∠DNE=90°，
∵∠GDE=90°，
∴∠EDN+∠GDN=90°，
∵∠PDG+∠GDN=90°，
∴∠EDN=∠PDG，
∵DE=DG，
∴△DPG≌△DNE，
∴PG=EN，
∵△ADE的面积=，△CDG的面积=，
∴△ADE的面积=△CDG的面积.

【点睛】
此题考查正方形的性质，三角形全等的判定及性质，利用三角形面积公式求解，根据图形得到三角形全等的条件是解题的关键.