浙教版九年级上册4.3 相似三角形当堂达标检测题

     浙教版数学九年级上册

           班级：                姓名：             

一、单选题

1．已知△ABC的三边长分别为4，3，6，与它相似的△DEF的最小边长为12，则△DEF的周长为（　　） 

A．39 B．26 C．52 D．13

【答案】C

【解析】∵△ABC的三边长分别为4，3，6，

∴△ABC的周长为：4+3+6=13，

∵与它相似的△DEF的最小边长为12，

∴△DEF的周长：△ABC的周长=12：3=4：1，

∴△DEF的周长为：4×13=52．

2．如图，△ABC∽△A′B′C′，AB=3，A′B′=4．若S△ABC=18，则S△A′B′C′的值为（　　）
 

A． B． C．24 D．32

【答案】D

【解析】由于相似三角形的面积比等于相似比的平方，且已知了两个相似三角形的对应边AB、A′B′的长，即可根据△ABC的面积和两个三角形的面积比求出S△A′B′C′的值．

3．若△ABC∽△A′B′C′，∠A=20°，∠C=120°，则∠B′的度数为（　　） 

A．20° B．30° C．40° D．120°

【答案】C

【解析】解：∵∠A=20°，∠C=120°， 

∴∠B=180°﹣∠A﹣∠C=40°，

∵△ABC∽△A′B′C′，

∴∠∠B′=∠B=40°．

4．如图，在平行四边形ABCD中，E为CD上一点，DE：CE＝2：3，连接AE，BD交于点F，则S△DEF：S△ADF：S△ABF等于（　　） 

A．2：3：5 B．4：9：25 C．4：10：25 D．2：5：25

【答案】C

【解析】解：∵四边形ABCD是平行四边形，

∴DC＝AB，DC∥AB，

∵DE：CE＝2：3，

∴DE：AB＝2：5，

∵DC∥AB，

∴△DEF∽△BAF，

∴ ＝（ ）2＝ ， ＝ ＝ ，

∴ ＝ ＝ ＝ （等高的三角形的面积之比等于对应边之比），

∴S△DEF：S△ADF：S△ABF等于4：10：25，

5．若两个相似三角形的面积之比为1：4，则它们的周长之比为（　　） 

A．1：2 B．1：4 C．1：5 D．1：16

【答案】A

【解析】解：∵两个相似三角形的面积之比为1：4， 

∴它们的相似比为1：2，

∴它们的周长之比为1：2．

6．一个三角形三边的长分别为3，5，7，另一个与它相似的三角形的最长边是21，则其它两边的和是（　　） 

A．17 B．19 C．21 D．24

【答案】D

【解析】解答：设另一个三角形的最短边为x，第二短边为y，

根据相似三角形的三边对应成比例，得

，

∴x=9，y=15，

∴x+y=24．

7．将直角三角形的三条边长同时扩大同一倍数，得到的三角形是（　　）

A．钝角三角形 B．锐角三角形 C．直角三角形 D．等腰三角形

【答案】C

【解析】解：将直角三角形的三条边长同时扩大同一倍数，得到的三角形与原三角形相似，因而得到的三角形是直角三角形．

二、填空题

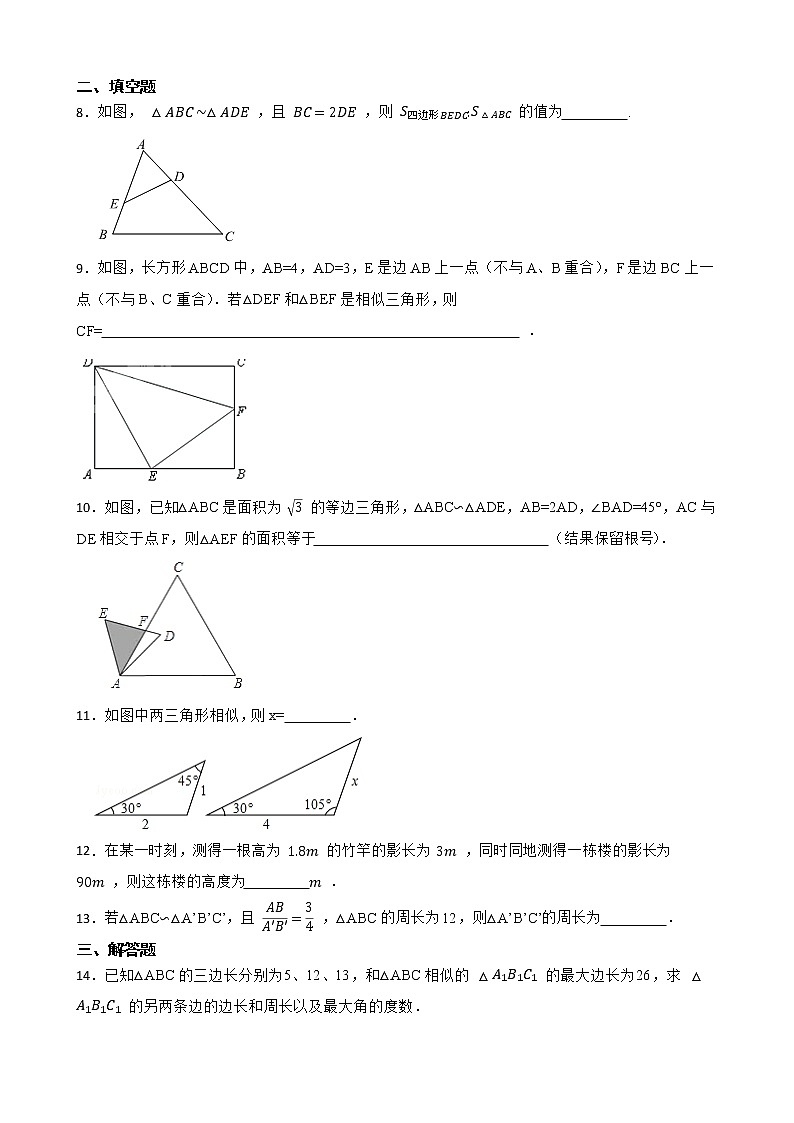
8．如图， ，且 ，则 的值为　     　.

【答案】

【解析】解：∵ ，且

∴

∴

设 ，则

∴

∴

9．如图，长方形ABCD中，AB=4，AD=3，E是边AB上一点（不与A、B重合），F是边BC上一点（不与B、C重合）．若△DEF和△BEF是相似三角形，则CF=　                                                     　 ．
 

【答案】或

【解析】

①当∠DEF=90°时，设AE=x，则BE=4﹣x，
易求△ADE∽△BEF，
∴，
即，
∵△DEF和△BEF是相似三角形，
∴△DEF和△ADE是相似三角形，
∴或，
∴或，
整理得，6x=12或x2﹣4x+9=0（无解），
解得x=2，
∴BE=4﹣2=2，
，
解得BF=，
CF=3﹣=；
②当∠DFE=90°时，设CF=x，则BF=3﹣x，
易求△BEF∽△CFD，
∴，
即，
∵△DEF和△BEF是相似三角形，
∴△DEF和△DCF是相似三角形，
∴或，
即或，
整理得，8x=12或x2﹣3x+16=0（无解），
解得x=；
综上所述，CF的值为或．

10．如图，已知△ABC是面积为 的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点F，则△AEF的面积等于　                            　（结果保留根号）． 

【答案】

【解析】解：∵△ABC∽△ADE，AB=2AD， 

∴ = ，

∵AB=2AD，S△ABC= ，

∴S△ADE= ，

如图，在△EAF中，过点F作FH⊥AE交AE于H，

∵∠EAF=∠BAD=45°，∠AEF=60°，

∴∠AFH=45°，∠EFH=30°，

∴AH=HF，

设AH=HF=x，则EH=xtan30°= x．

又∵S△ADE= ，

作CM⊥AB交AB于M，

∵△ABC是面积为 的等边三角形，

∴ ×AB×CM= ，

∠BCM=30°，

设AB=2k，BM=k，CM= k，

∴k=1，AB=2，

∴AE= AB=1，

∴x+ x=1，

解得x= = ．

∴S△AEF= ×1× = ．

11．如图中两三角形相似，则x=　     　．

【答案】

【解析】解：如图所示：

∵四边形ABCD与四边形EFGH位似，

∴△OEF∽△OAB，△OFG∽△OBC，

∴ = = ，

∴ = =

12．在某一时刻，测得一根高为 的竹竿的影长为 ，同时同地测得一栋楼的影长为 ，则这栋楼的高度为　     　 ．  

【答案】54

【解析】解：设这栋楼的高度为hm，

∵在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一栋楼的影长为60m，

∴ ，

解得h=54（m）．

13．若△ABC∽△A’B’C’，且 ，△ABC的周长为12，则△A’B’C’的周长为　     　．  

【答案】16

【解析】解：∵ △ABC∽△A’B’C’，
∴，
∵，C△ABC=12，
∴C△A´B´C´=12×=16.

三、解答题

14．已知△ABC的三边长分别为5、12、13，和△ABC相似的 的最大边长为26，求 的另两条边的边长和周长以及最大角的度数．

【答案】解：∵△ABC的相似三角形 的最大边长为26，即对应△ABC的对应最大边长13，所以对应边长的比值为2，所以另两边分别为10，24，故三角形的周长为10+24+26=60．

∵ ，∴三角形的最大角度为90°

【解析】根据相似三角形的性质可求得△的另外两边长；根据三角形的周长=三边之和可求周长；根据勾股定理的逆定理可求得三角形的最大角度为90°。

15．如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？

【答案】解：设在开始运动后第x秒，△BPQ与△BAC相似，

由题意得：AP＝2xcm，PB＝（8﹣2x）cm，BQ＝4x，

分两种情况考虑：

当∠BPQ＝∠C，∠B＝∠B时，△PBQ∽△CBA，

∴ ，

即

解得：x＝0.8，

当x＝0.8秒时，△BPQ与△BAC相似；

当∠BPQ＝∠A，∠B＝∠B时，△BPQ∽△BAC，

∴ ，即 ，

解得：x＝2，

当x＝2秒时，△BPQ与△BAC相似.

综上，当x＝0.8秒或2秒时，△BPQ与△BAC相似.

【解析】设在开始运动后第x秒，△BPQ与△BAC相似，由题意得：AP＝2xcm，PB＝(8-2x)cm，BQ＝4x，然后分①∠BPQ＝∠C，∠B＝∠B时，△PBQ∽△CBA；②∠BPQ＝∠A，∠B＝∠B时，△BPQ∽△BAC，利用相似三角形对应边成比例就可求出x的值.

16．如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE∽△DEF，AB=6，AE=9，DE=2，求EF的长．

【答案】解答：∵四边形ABCD是矩形， 

∴∠BAE=90°，

∵AB=6，AE=9，

∴BE =  =  =  ，

∵△ABE∽△DEF，

∴，即   ，

解得EF=  ．

【解析】先根据勾股定理求出BE的长，再根据相似三角形的对应边成比例即可求出EF的长．

17．如图，D为△ABC边AB上一点，且CD分△ABC为两个相似比为1：的一对相似三角形；（不妨如图假设左小右大），求：

（1）△BCD与△ACD的面积比；

（2）△ABC的各内角度数．

【答案】解：（1）∵△BCD和△CAD的相似比为1：，

∴△BCD和△CAD的面积比为1：3；

（2）∵△BCD∽△CAD，

∴∠BDC=∠ADC=90°，

tanA===，

∴∠A=30°，

tanB==，

∴∠B=60°，

∴∠ACB=90°．

【解析】（1）根据相似三角形面积的比等于相似比的平方解答；

（2）根据锐角三角函数的概念解答即可．