






初中数学浙教版九年级上册4.3 相似三角形获奖课件ppt
展开4.3相似三角形 教案
课题 | 4.3相似三角形 | 单元 | 第四单元 | 学科 | 数学 | 年级 | 九年级(上) |
学习 目标 | 1.理解相似三角形的概念,并能表示两个三角形相 似; 2.掌握相似三角形的性质,并能利用相似三角形的性 质求计算角度和线段长度. | ||||||
重点 | 相似三角形的概念. | ||||||
难点 | 在具体的图形中找出相似三角形的对应边,并写出比例式,需要学生具有一定的分辨能力,是本节教学的难点. | ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
导入新课 | 一、创设情景,引出课题
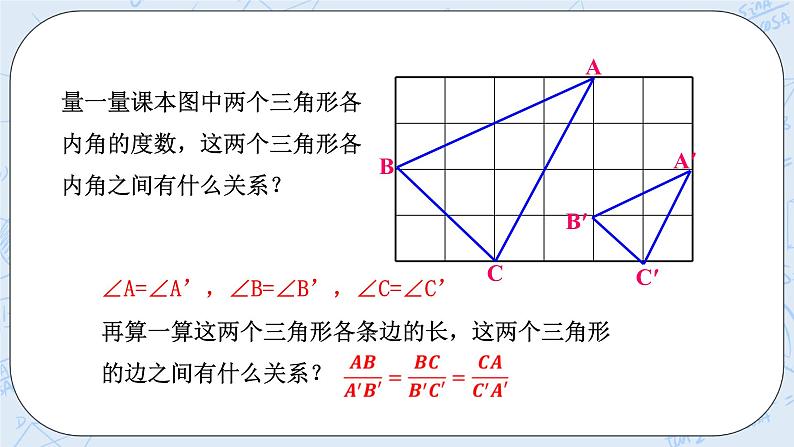
图中的这些三角形有什么特点? 一些奇妙的曲线与相似三角形有着密切的联系 请同学们在草稿本画一个30度的直角三角形.
然后和同桌进行比较你们所画的三角形,你发现了什么? ∠A=∠A’,∠B=∠B’,∠C=∠C’
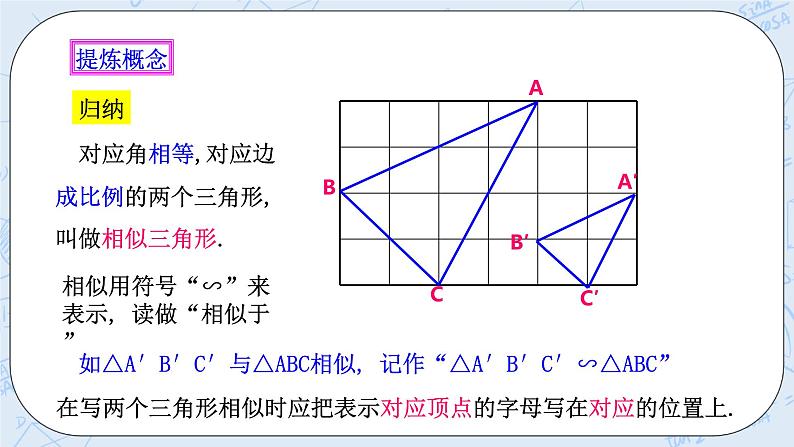
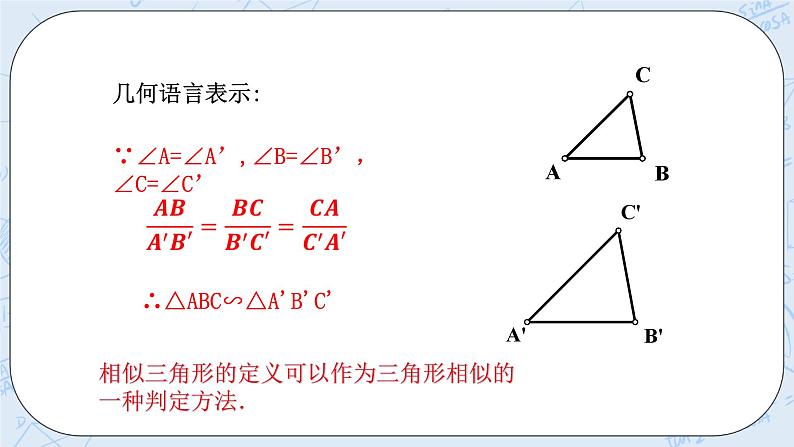
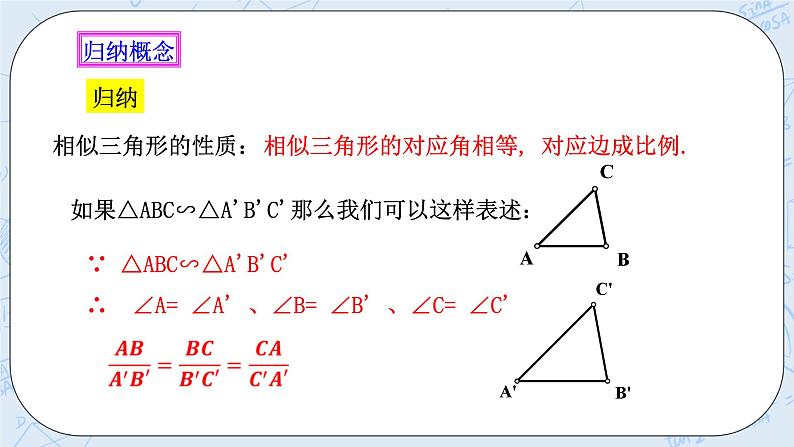
二、提炼概念 归纳 对应角相等,对应边成比例的两个三角形,叫做相似三角形. 相似用符号“∽”来表示, 读做“相似于” 如△A′B′C′与△ABC相似, 记作“△A′B′C′∽△ABC” 在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上. 几何语言表示: ∵∠A=∠A’,∠B=∠B’,∠C=∠C’
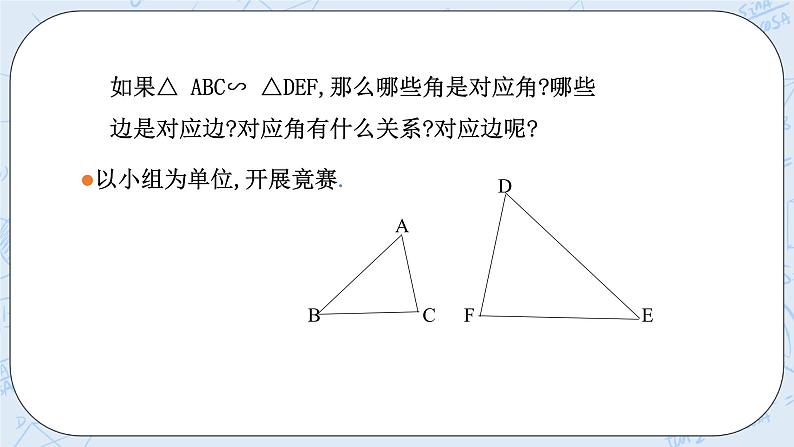
∴△ABC∽△A'B'C' 归纳 相似三角形的性质:相似三角形的对应角相等, 对应边成比例. 如果△ABC∽△A'B'C'那么我们可以这样表述: ∵ △ABC∽△A'B'C' ∴ ∠A= ∠A' 、∠B= ∠B' 、∠C= ∠C' 三、典例精讲 例1:
例2、已知: 如图, D、E分别是△ABC的AB, AC边上的点, △ABC∽△ADE.已知 AD:DB=1:2, BC=9cm, 求DE的长.
| 思考 自议 让他们经历相似三角形概念的发生过程,在说明角对应相等时有两种方法:一是通过测量,二是推理.
|
利用类比全等三角形的概念与性质理解相似三角形 的概念与性质;
|
讲授新课 |
|
相似三角形的概念可以作为判定三角形相似的方法. | 相似三角形的对应边成比例、对应角相等是相似三 角形最基本的性质.
|
课堂检测 | 四、巩固训练
①=;②=; ③=;④=.
A.1个 B.2个 C.3个 D.4个 答案:A 2.如图,已知△ABC,D,E分别是AB,AC边上的点.AD=3 cm,AB=8 cm,AC=10 cm.若△ADE与△ABC相似,则AE的值为 ( ) A. cm B. cm或 cm C. cm或 cm D.cm 答案:C 【解析】连结DE,∵△ADE与△ABC相似, ∴AD∶AB=AE∶AC或AD∶AC=AE∶AB, ∴3∶8=AE∶10或3∶10=AE∶8, ∴AE=(cm)或(cm). 3.如图,已知△ABC∽△AED,AD=5 cm,AC=10 cm,AE=6 cm,∠A=66°,∠ADE=65°,求AB的长及∠C的度数. 解:∵△ABC∽△AED,∠ADE=65°,∴∠ADE=∠C=65°, ∵=,∴=,解得AB=12 cm. 4. 如图所示,△ABC ∽△ACD,且=,AD=4 cm,DC=6 cm.求AC和BC的长. 解:∵△ABC∽△ACD,∴=,=.∵=,AD=4 cm,DC=6 cm,∴=,=.即AC=6 cm,BC=9 cm.
|
|
|
课堂小结 |
|
|
|
初中数学浙教版九年级上册第4章 相似三角形4.3 相似三角形优秀ppt课件: 这是一份初中数学浙教版九年级上册第4章 相似三角形4.3 相似三角形优秀ppt课件,文件包含浙教版数学九上453相似三角形的性质及其应用课件pptx、浙教版数学九上453相似三角形的性质及其应用学案doc、浙教版数学九上453相似三角形的性质及其应用教案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学浙教版九年级上册4.3 相似三角形优质课课件ppt: 这是一份初中数学浙教版九年级上册4.3 相似三角形优质课课件ppt,文件包含浙教版数学九上452相似三角形的性质及其应用课件pptx、浙教版数学九上452相似三角形的性质及其应用教案doc、浙教版数学九上452相似三角形的性质及其应用学案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学浙教版九年级上册4.3 相似三角形精品课件ppt: 这是一份初中数学浙教版九年级上册4.3 相似三角形精品课件ppt,文件包含浙教版数学九上451相似三角形的性质及其应用课件pptx、浙教版数学九上451相似三角形的性质及其应用教案doc、浙教版数学九上451相似三角形的性质及其应用学案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。













