专题02函数的基本性质B辑-2022年高考数学压轴必刷题（第二辑）

2022年高考数学压轴必刷题（第二辑）

专题02函数的基本性质B辑

1．设是定义在上的函数，其导函数为，若，，则不等式（其中为自然对数的底数）的解集为（    ）

A． B．

C． D．

【答案】D

设，则，

函数单调递减，，故，

，即，即，故.

故选：D.

2．已知定义在上的函数满足：，某同学由此前提条件出发，然后又补充了一个附加条件，再经过推理，他得出四个结论，并且给其编号：①.若时，是奇函数且一定是单调增函数；②.若，是偶函数且有最大值为1；③.若，则；④.若，则.请你确认该同学做出的所有编号中其中正确的是（    ）

A．①③ B．①④ C．①②③ D．②③④

【答案】D

由已知关系式，

对于序号①，∵，故令，得，则，

∴是奇函数，设时，

由不能保证推出，

故序号①不能肯定成立；

对于序号②，∵时，令，则，进而有，

∴是偶函数，此时不妨特取，显然有，即满足，且有最大值1.

故序号②成立.

对于序号③来说，∵序号②正确，显然，有，故序号③C正确.

对于序号④，∵，特取，

则，

进而有，整理得①.

且有②

由①②得，推得，又得，

∴是最小正周期为6的周期函数，根据，特取，则得.

再取，即，

解得，令，.

于是，

解得.

∴.故序号④正确.

综上所述，本题正确的序号为②③④.

故选：D.

3．已知函数与的图象上存在两对关于直线对称的点，则的取值范围是（    ）

A． B． C． D．

【答案】B

∵ 函数与的图象上存在两对关于直线对称的点，∴ 函数与函数的图象有两个交点，即方程，有两解，

即方程，有两解，

令，，

则，

当时，，函数为减函数；

当时，，函数为增函数.

故当时，，

又，

所以当时，，

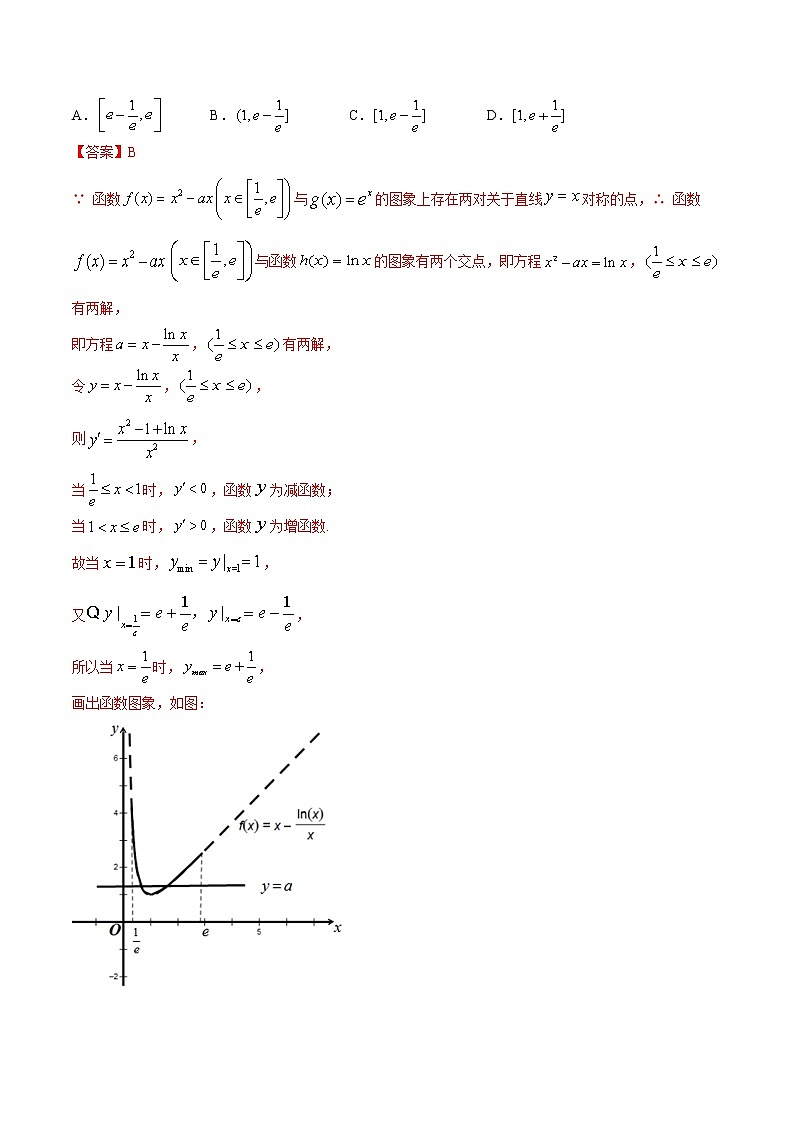
画出函数图象，如图：

由图可知的取值范围.

故选：B.

4．已知函数，对于，使得，则实数的取值范围是（    ）

A． B．

C． D．

【答案】C

对于，使得，等价于.

因为函数.

因为与在[0，1]上为增函数

所以函数在[0，1]上为增函数，

所以.

同理可知函数在[0，4]上为增函数，则.

则当时，，

于是由，得；

当时，，满足；

当时，，于是由，得.

综上可知，

故选：C.

5．已知函数是奇函数，且，若对，恒成立，则的取值范围是（    ）

A． B． C． D．

【答案】A

因为函数是奇函数，

所以函数是偶函数.

，

即，

又，

所以，.

函数的定义域为，所以，

则函数在上为单调递增函数.又在上，

，所以为偶函数，且在上单调递增.

由，

可得，对恒成立，

则，对恒成立，，

得，

所以的取值范围是.

故选：A.

6．对于定义域为的函数，如果存在区间满足是上的单调函数，且在区间上的值域也为，则称函数为区间上的“保值函数”，为“保值区间”．根据此定义给出下列命题：①函数是上的“保值函数”；②若函数是上的“保值函数”，则；③对于函数存在区间，且，使函数为上的“保值函数”．其中所有真命题的序号为（    ）

A．② B．③ C．①③ D．②③

【答案】D

由“保值函数”定义可知为区间上的“保值函数”则在上是单调函数且在区间时其值域也为，那么当函数为增函数时满足条件在上有两个不同的实数解，的函数就是“保值函数”，

命题①中，虽满足在上单调但值域为，不是，故①为假命题；

②中由的图象可知，函数在上单调且值域为，其为区间上的“保值函数”故②为真命题；

③中，则由在成立，所以为上的增函数，再由解得有两个根，，构造函数，是减函数，，，由零点存在性定理知存在，使成立，故③为真命题．综上所有真命题的序号为②③，

故选：D．

7．若存在实数，对任意，不等式恒成立，则实数的取值范围是（    ）

A． B． C． D．

【答案】B

对任意，不等式恒成立，

等价于不等式恒成立，

等价于恒成立，

等价于恒成立，

等价于函数的图象和函数的图象分别位于直线的两侧

在直角坐标系内画出函数和函数的图象如图所示，

由解得,

所以两个函数图象的横坐标较小的交点坐标为，

由图易得当时，取得最大值，令，解得，

所以的取值范围为，

故选：B

8．函数．若存在，使得，则的取值范围是（    ）．

A． B． C． D．

【答案】D

当时，，因此，可化为，即存在，使成立，由于的对称轴为，所以，当单调递增，因此只要，即，解得，又因，所以，当时，，，满足题意，

综上，．

故选：．

9．设函数由方程确定，对于函数给出下列命题：

①存在，，使得成立；

②，，使得且同时成立；

③对于任意，恒成立；

④对任意，，；都有恒成立．

其中正确的命题共有（    ）

A．1个 B．2个 C．3个 D．4个

【答案】A

由方程知，

当且时，方程为；

当且时，方程为，不成立；

当且时，方程为；

当且时，方程为，不成立；

作出函数的图象如图所示，

对于①，是定义域R上的单调减函数，

则对任意，都有恒成立，①错误；

对于②，假设点在第一象限，则点也在第一象限，

所以，该方程组没有实数解，所以该情况不可能；

假设点在第四象限，则点在第二象限，

所以，该方程组没有实数解，所以该种情况不可能；

同理点在第二象限，则点在第四象限，也不可能．

故该命题是假命题．

对于③，由图形知，对于任意，有

即恒成立，③正确；

对于④，不妨令，

则为，

又由题，则 ，

即不恒成立，所以④错误．

综上知，正确的命题序号是③．

故选：A

10．设函数，函数的图象与的图象关于直线对称．若实数，满足，且有极小值，则实数的值是（    ）．

A．3 B．2 C．1 D．

【答案】B

设为函数的图象上任意一点，

则关于直线对称点为在函数的图象上，

所以，

即，

令，

则，，

所以，

则，

令，得，

当时，，函数为减函数，

当时，，函数为增函数，

所以当，有极小值，

解得，

故选：B

11．若不等式．对x∈恒成立，则sin(a+b)和sin(a-b)分别等于（    ）

A． B． C． D．

【答案】D

由，则，

当或时，即或时，，

当时，即时，，

所以当或时，，

当时，，

设函数，则在上单调递增，在上单调递减，

且函数的图象关于直线对称，所以，

所以，解得，

又由，解得，

所以，.

故选：D.

12．函数是定义域为的奇函数，且它的最小正周期是T，已知，.给出下列四个判断：①对于给定的正整数，存在，使得成立；②当a时，对于给定的正整数，存在，使得成立；③当时，函数既有对称轴又有对称中心；④当时，的值只有0或.其中正确判断的有(    )

A．1个 B．2个 C．3个 D．4个

【答案】C

对于①，要使成立，

即，

当时，，

，故，故①正确；

对于②，要使成立，

即，

取，此时

，故②正确；

对于③④，当时，为将右移个单位，此时周期变为，既有对称轴也有对称中心，值域为，

当时，为将右移个单位，此时，

当时，为将右移个单位，此时，故③正确，④错误；

故选：C.

13．当时，函数恒成立，则的最大值为（    ）

A． B．2 C． D．1

【答案】C

解：由题可知，时，函数恒成立，

即为恒成立，

设，即，

为最小正周期为2的函数，且，，

设，可得，

分别作出和的图象，可得它们有两个交点，，，

由题意可得当，时，恒成立，即恒成立，

此时取得最大值.

故选：C.

14．函数，若存在正实数，其中且，使得，则的最大值为（    ）

A．6 B．7 C．8 D．9

【答案】C

，

当时，，，

，，

即，所以，

，

由知，

集合，

因为且，所以，，

所以，即，又，

所以的最大值为8.

故选：C．

15．已知是定义在R上的奇函数，当时，.对于任意不小于2的正整数n，当时，都满足.给出以下命题：

①的值域为；

②当时，；

③当时，方程有且只有三个实根.

以上三个命题中，所有真命题的序号是（    ）

A．①② B．①③ C．②③ D．①②③

【答案】A

因为当时，都满足

所以当时，

，

当时，

，

从而类推可得当时，

当时，，即②正确；

当时，

因为是定义在R上的奇函数，所以，即①正确；

当时，由图可知 不止三个交点，所以③错误；

故选：A

16．定义域均为D的三个函数，，满足条件：对任意，点与点都关于点对称，则称是关于的“对称函数”.已知函数，，是关于的“对称函数“，记的定义域为D，若对任意，都存在，使得成立，则实数a的取值范围是（    ）

A．. B．. C．. D．.

【答案】C

解：由函数，，是关于的“对称函数”，

可得，，，，

可得的解为，

由，（1），，

且在递增，，递减，可得的最小值为，最大值为1，

可得的值域为，，

而在，递增，可得的值域为，，

由题意可得，，，

即有，即为，

解得或，

则的范围是，

故选：．

17．定义函数为不大于的最大整数，对于函数有以下四个命题：①；②在每一个区间，上，都是增函数；③；④的定义域是，值域是.其中真命题的序号是（    ）.

A．③④ B．①③④ C．②④ D．①②④

【答案】D

画出的图象如图所示，

由函数的图象可知，是最小正周期为1的函数，且当时，，

所以，所以①②④都正确，

而，，所以③错误.

故选：D

18．若函数在其图象上存在不同的两点，其坐标满足条件：的最大值为0，则称为“柯西函数”，则下列函数：

①；②；③；④．其中是“柯西函数”的为（    ）

A．①② B．③④ C．①③ D．②④

【答案】B

由柯西不等式得，对任意实数恒成立，

当且仅当时取等号，

若函数在其图象上存在不同的两点，

其坐标满足条件：的最大值为0，

则函数在其图象上存在不同的两点，使得共线，

即存在过原点的直线与的图象有两个不同的交点．

对于①，方程，即，最多有1个正根，所以不是柯西函数；对于②，由图①可知不存在；因为在点处，与相切，所以最多有1个正解；

对于③，由图②可知存在；对于④，由图③可知存在．所以①②不是柯西函数，③④是柯西函数．

19．把方程表示的曲线作为函数的图象，则下列结论正确的是（    ）

①在R上单调递减

②的图像关于原点对称

③的图象上的点到坐标原点的距离的最小值为3

④函数不存在零点

A．①③ B．①②③ C．①③④ D．①②③④

【答案】C

，当，时不成立；当，时，；

当，时，；当，时，；

画出图像，如图所示：

由图判断函数在R上单调递减，故①正确，②错误.

由图判断图象上的点到原点距离的最小值点应在，的图象上，

即满足，设图象上的点，

，当时取最小值3，故③正确；

当，即，函数的零点，就是函数和的交点，而是曲线，，和，，的渐近线，所以没有交点，

由图象可知，和，，没有交点，

所以函数不存在零点，故④正确.

故选：C.

20．设定义在上的函数单调递增恒成立，且满足，则（    ）

A． B． C． D．

【答案】A

若，则，

即，

因为函数在上单调递增且，所以，

而与矛盾，故，排除B、C；

若，则，

即，

因为函数在上单调递增且，所以，

而与矛盾，故排除D.

故选：A

21．若函数，则（    ）

A．

B．

C．

D．

【答案】A

解：依题意，，

因为，故函数关于直线对称，

令，且，为偶函数.

，

可知：当时，，故；

当时，，故，

故函数在上单调递增，又因为为偶函数，故在上单调递减，

所以函数在上单调递减，在上单调递增，

因为，

，，

即.

故选：A.

22．定义在上的连续函数，导函数为．若对任意不等于的实数，均有成立，且，则下列命题中一定成立的是（    ）

A． B．

C． D．

【答案】B

构造函数，则，

当时，.

当时，则，；

当时，则，.

所以，函数在上单调递增，在上单调递减.

又，所以，

即，故函数的图象关于直线对称．

对于A选项，，即，与的大小关系不确定，A选项错误；

对于B选项，，即，即，B选项正确；

对于C、D选项，，即，C、D选项错误.

故选：B．

23．已知函数，其中，记为的最小值，则当时，的取值范围为（    ）

A． B． C． D．

【答案】D

①当时，在上单调递增，

所以，因此满足题意；

②当时，在上单调递增，在上单调递减

因此⑴当时，在上单调递增，所以

，

或或

⑵当时，在上单调递增，在上单调递减，

所以；

综上，的取值范围为，

故选：D

24．已知函数对任意的，都有，函数是奇函数，当时，，则函数在区间内的零点个数为（    ）

A．8 B．7 C．6 D．5

【答案】A

解：∵函数是奇函数

∴函数的图象关于点对称

∴把函数的图象向右平移1个单位可得函数的图象，即函数的图象关于点对称，即满足

又∵

∴，从而

∴，即

∴函数的周期为2，且图象关于直线对称.

画出函数的图象如图所示：

结合图象可得区间内有8个零点.

故选：A.

25．定义为中的最大值，设，则的最小值是（    ）

A．2 B．3 C．4 D．6

【答案】C

【解析】

画出函数的图象，如图

由图可知，函数在 处取得最小值，即的最小值为，故选B.

26．已知定义域为的函数的图像关于原点对称，且，若曲线在处切线的斜率为4，则曲线在处的切线方程为（    ）

A． B． C． D．

【答案】B

因为定义域为的函数的图像关于原点对称，所以，

因为，，两式相减可得，，故，故；

因为，故所求切线方程为，

故选：B．

27．已知函数，若，则实数的取值范围是（    ）

A． B．

C． D．

【答案】A

由函数的解析式可得函数为奇函数，绘制函数图像如图所示，

则不等式即，即，

观察函数图像可得实数的取值范围是.

故选A.

28．已知单调函数的定义域为，对于定义域内任意，，则函数的零点所在的区间为（  ）

A． B． C． D．

【答案】C

根据题意，对任意的，都有，又由是定义在上的单调函数，则为定值，设，则，又由，∴，所以，所以，所以，因为，所以零点所在的区间为（3，4）.

29．已知函数若存在实数满足，其中，则的取值范围是（   ）

A． B． C． D．

【答案】B

画出 图象，如图，

，

由二次函数的性质可得，

由图可知，，

，

，

，

，

即的取值范围是，故选B.

30．已知函数是定义在上的奇函数，且当时，，则方程的所有解的和为（　　）

A． B．1 C．3 D．5

【答案】C

∵是定义在R上的奇函数，且当时，

∴当时，

则

即

则

作出的图象如图：

∵的图象与的图象关于对称

∴作出的图象，由图象知与的图象有三个交点

即有三个根，其中一个根为1，另外两个根a，b关于对称

即

则所有解的和为

故选C．