期末复习综合测试题（4）-【新教材】人教A版（2019）高中数学必修第一册

必修第一册综合测试题四

一．选择题（共12小题）

1．函数定义域为　　

A． B． C．， D．，

2．已知全集为实数集，，，则　　

A． B． C． D．

3．关于的方程有实数解的充要条件是　　

A． B． C． D．

4．已知命题：“，”，若为真命题，则实数的取值范围是　　

A． B． C．， D．，

5．不等式的解集是，，则等于　　

A． B．14 C． D．10

6．已知实数，，且，则的最小值为　　

A． B． C． D．

7．已知函数，若关于的方程恰有3个不同的实数根，则实数的取值范围为　　

A． B．， C． D．，

8．刘徽（约公元225年年），魏晋期间伟大的数学家，中国古典数学理论的奠基人之一．他在割圆术中提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这可视为中国古代极限观念的佳作．割圆术的核心思想是将一个圆的内接正边形等分成个等腰三角形（如图所示），当变得很大时，这个等腰三角形的面积之和近似等于圆的面积，运用割圆术的思想得到的近似值为　　

A． B． C． D．

二．多选题（共4小题）

9．已知集合，，若对于任意，，存在，，使得成立，则称集合是“完美对点集”．给出下列四个集合：

①；

②；

③；

④．

其中是“完美对点集”的序号为　　

A．① B．② C．③ D．④

10．已知，为正实数，且，则　　

A．的最大值为 B．的最小值为 

C．的最小值为4 D．的最大值为

11．已知定义在上的函数满足，且当时，，则可作为方程实根的有　　

A． B． C． D．

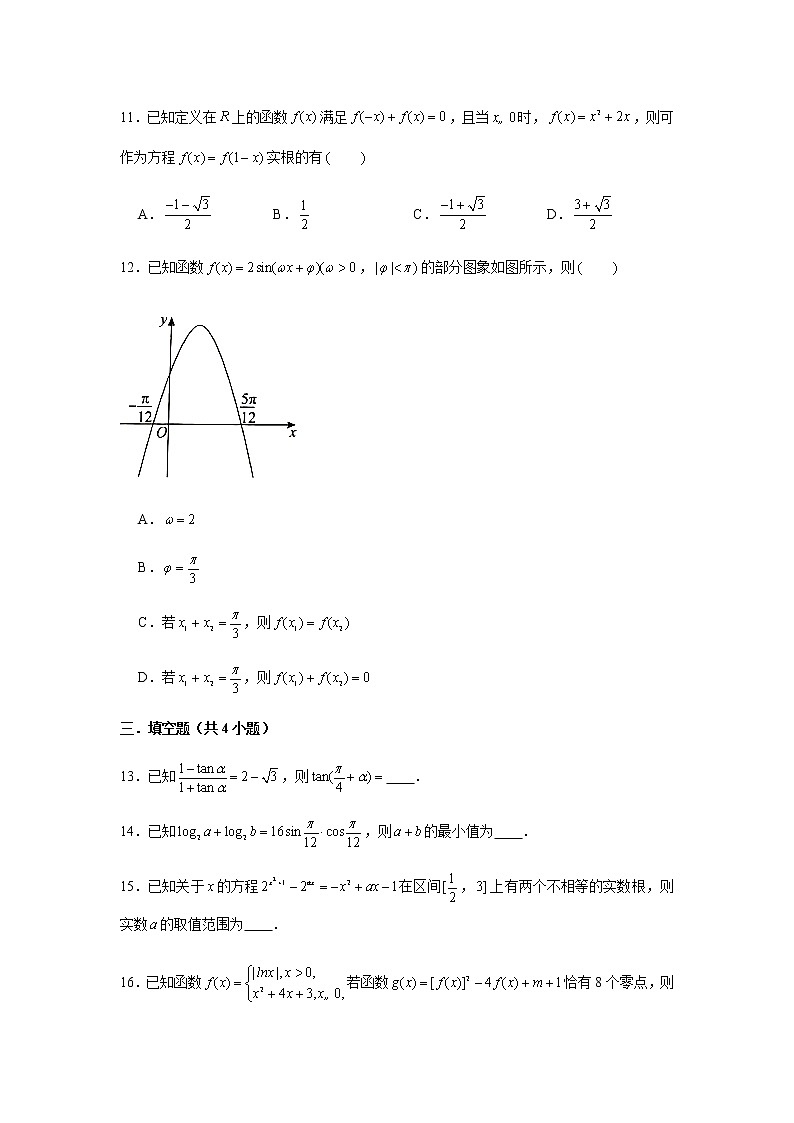
12．已知函数，的部分图象如图所示，则　　

A． 

B． 

C．若，则 

D．若，则

三．填空题（共4小题）

13．已知，则　　．

14．已知，则的最小值为　　．

15．已知关于的方程在区间，上有两个不相等的实数根，则实数的取值范围为　　．

16．已知函数若函数恰有8个零点，则的范围为　　．

四．解答题（共6小题）

17．已知函数．

（1）求的值及函数的单调增区间；

（2）若，，不等式恒成立，求实数的取值集合．

18．已知函数为常数）是奇函数．

（1）求的值；

（2）函数，若函数有零点，求参数的取值范围．

19．某公园欲将如图所示的一块矩形空地进行重新规划，拟在边长为的正方形内种植红色郁金香，正方形的剩余部分（即四个直角三角形内）种植黄色郁金香．现要将以为一边长的矩形改造为绿色草坪，要求绿色草坪的面积等于黄色郁金香的面积，设，．

（1）求与之间的函数关系式；

（2）求的最大值．

20．已知函数．

（1）证明：函数在，上单调递减；

（2）解关于的不等式；

（3）求函数的值域．

21．已知奇函数．

（1）求的值，并求函数的值域；

（2）若函数在区间，上有两个不同的零点，求的取值范围．

22．已知命题：关于的方程有两个大于1的实数根．

（1）若命题为真命题，求实数的取值范围；

（2）命题，是否存在实数使得是的必要不充分条件，若存在，求出实数的取值范围；若不存在，说明理由．

必修第一册综合测试题四

参考答案与试题解析

一．选择题（共12小题）

1．函数定义域为　　

A． B． C．， D．，

【分析】根据二次根式以及对数函数的性质求出函数的定义域即可．

【解答】解：由题意得：，

解得：，

故选：．

2．已知全集为实数集，，，则　　

A． B． C． D．

【分析】可求出集合，然后进行补集和交集的运算即可．

【解答】解：，，

，．

故选：．

3．关于的方程有实数解的充要条件是　　

A． B． C． D．

【分析】由，得的取值范围，逐项判断即可求得答案．

【解答】解：因为，

所以关于的方程有实根的充要条件是．

故选：．

4．已知命题：“，”，若为真命题，则实数的取值范围是　　

A． B． C．， D．，

【分析】直接利用存在性问题和真值表的应用求出结果．

【解答】解：命题：“，”，若为真命题，

所以，即．

故选：．

5．不等式的解集是，，则等于　　

A． B．14 C． D．10

【分析】由不等式的解集，可求对应方程的根，求出、，然后求出．

【解答】解：因为

所以是方程的根，

所以

， 所以

故选：．

6．已知实数，，且，则的最小值为　　

A． B． C． D．

【分析】利用“乘1法”与基本不等式的性质即可得出．

【解答】解：，，且，

，

则

．

当且仅当且，

即时取等号．

的最小值为．

故选：．

7．已知函数，若关于的方程恰有3个不同的实数根，则实数的取值范围为　　

A． B．， C． D．，

【分析】先根据函数的解析式作出函数的图象，然后利用换元法将关于的方程恰有3个不同的实数根，转化为有两个不同的实数根，且，，，然后再利用二次方程根的分布列出不等式组，求解即可得到答案．

【解答】解：因为函数，作出函数图象如图所示，

因为关于的方程恰有3个不同的实数根，

所以令，根据图象可得，有两个不同的实数根，且，，，

记，则有，

解得，

所以实数的取值范围为．

故选：．

8．刘徽（约公元225年年），魏晋期间伟大的数学家，中国古典数学理论的奠基人之一．他在割圆术中提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这可视为中国古代极限观念的佳作．割圆术的核心思想是将一个圆的内接正边形等分成个等腰三角形（如图所示），当变得很大时，这个等腰三角形的面积之和近似等于圆的面积，运用割圆术的思想得到的近似值为　　

A． B． C． D．

【分析】取正60边形，设半径为1，利用等腰三角形的面积计算公式、圆的面积计算公式得出方程，即可得出的近似值．

【解答】解：取正60边形，设半径为1，则，解得．

故选：．

二．多选题（共4小题）

9．已知集合，，若对于任意，，存在，，使得成立，则称集合是“完美对点集”．给出下列四个集合：

①；

②；

③；

④．

其中是“完美对点集”的序号为　　

A．① B．② C．③ D．④

【分析】利用数形结合的方法解决，根据题意，若集合，是“完美对点集”，就是在函数图象上任取一点，得直线，过原点与垂直的直线，若总与函数图象相交即可．

【解答】解：对于①，是以，轴为渐近线的双曲线，渐近线的夹角是，所以在同一支上，任意，，不存在，，满足“完美对点集”的定义；在另一支上对任意，，不存在，，使得成立，所以不满足“完美对点集”的定义，不是“完美对点集”．

对于②，，对于任意，，存在，，使得成立，例如、，，满足“完美对点集”的定义，所以是“完美对点集”；

对于③，，取点，曲线上不存在另外的点，使得两点与原点的连线互相垂直，所以集合不是“完美对点集”．

对于④，，如下图红线的直角始终存在，对于任意，，存在，，使得成立，例如取，则，满足“完美对点集”的定义，所以是“完美对点集”；正确．

故答案为：②④．

故选：．

10．已知，为正实数，且，则　　

A．的最大值为 B．的最小值为 

C．的最小值为4 D．的最大值为

【分析】由不等式可分析选项，由不等式可分析选项，由已知得出，通过恒等变形以及基本不等式可分析，．

【解答】解：对于选项，，即，

又，为正实数，所以，即，当且仅当时，不等式可取等号，故正确；

对于选项，，即，

又，为正实数，所以，当且仅当时，不等式可取等号，故正确；

对于选项，，，

，

当且仅当，即，时，不等式可取等号，故错误；

对于选项，，，

即，

当且仅当，即，时，不等式可取等号，故正确；

故选：．

11．已知定义在上的函数满足，且当时，，则可作为方程实根的有　　

A． B． C． D．

【分析】由已知求得函数解析式，得到，进一步写出分段函数，求解方程得答案．

【解答】解：，为定义在上的奇函数，

当时，，设，则，

得，即．

，则，

令，

当时，解得或或．

故选：．

12．已知函数，的部分图象如图所示，则　　

A． 

B． 

C．若，则 

D．若，则

【分析】由周期求出，由五点法作图求出的值，可得函数的解析式，再利用正弦函数的图象和性质，得出结论．

【解答】解：根据函数，的部分图象，，

，，故正确．

为其图象的一条对称轴，故有，，，故错误．

为其图象的一条对称轴，故若，则有，故正确，错误，

故选：．

三．填空题（共4小题）

13．已知，则　　．

【分析】利用两角和的正切公式即可得解．

【解答】解：因为，

所以．

故答案为：．

14．已知，则的最小值为　8　．

【分析】由已知结合对数的运算性质及二倍角公式进行化简可求，然后结合基本不等式即可求解．

【解答】解：因为，

所以，

故，

则，

当且仅当时取等号，的最小值8．

故答案为：8．

15．已知关于的方程在区间，上有两个不相等的实数根，则实数的取值范围为　　．

【分析】观察方程的结构特征，将它进行变形为，然后构造函数，确定函数的单调性，从而将问题转化为当时，有两个不相等的实数根，利用根的分布列出不等式组，求解即可得到答案．

【解答】解：因为方程，

所以变形为，

令，

则有，

因为在上单调递增，

所以即为，

故当时，有两个不相等的实数根，

在中，则有，即，

解得，

所以实数的取值范围为．

故答案为：．

16．已知函数若函数恰有8个零点，则的范围为　　．

【分析】利用分段函数的解析式，先作出函数的图象，然后利用换元法将函数恰有8个零点转化为方程在，必有两个不等的实数根，再结合图象分析即可得到答案．

【解答】解：画出函数的图象如图所示，

设，由，得，

因为有8个零点，

所以方程有4个不同的实根，

结合的图象可得在，内有4个不同的实根，

所以方程必有两个不等的实数根，

即在，内有2个不同的实根，

结合图象可知，

则有，解得，

所以的范围为．

故答案为：．

四．解答题（共6小题）

17．已知函数．

（1）求的值及函数的单调增区间；

（2）若，，不等式恒成立，求实数的取值集合．

【分析】（1）利用三角函数恒等变换的应用化简函数解析式，代入计算可求的值，结合正弦函数的单调性列出不等式解出单调区间；

（2）求出在，上的值域，根据题意列出不等式组即可解出的范围．

【解答】解：（1），

，

令，解得，．

的单调递增区间是，，．

（2），，可得，，

当时，取得最大值1，当时，取得最小值．

恒成立，，解得．

实数的取值范围是，．

18．已知函数为常数）是奇函数．

（1）求的值；

（2）函数，若函数有零点，求参数的取值范围．

【分析】（1）根据题意，求出函数的定义域，由奇函数的定义域可得，即，变形分析可得答案，

（2）若函数有零点，则直线与曲线有交点，分析的值域，即可得，，，解可得的取值范围，即可得答案．

【解答】解：（1）根据题意，函数，则有，解可得，

即函数的定义域为，，，

根据奇函数的定义，对于，，，则有，

即，化简得：即；

（2）若函数有零点，则直线与曲线有交点，

又由，那么，则的值域为，，；

故由，，，

解得：，

即的取值范围为：，，．

19．某公园欲将如图所示的一块矩形空地进行重新规划，拟在边长为的正方形内种植红色郁金香，正方形的剩余部分（即四个直角三角形内）种植黄色郁金香．现要将以为一边长的矩形改造为绿色草坪，要求绿色草坪的面积等于黄色郁金香的面积，设，．

（1）求与之间的函数关系式；

（2）求的最大值．

【分析】（1）通过求解三角形推出，，，结合面积关系，推出的不等式即可．

（2）令，则，化简函数的解析式，结合函数的单调性求解函数最值即可．

【解答】解：（1）在中，，则，

同理在中，，则，

，，

绿色草坪的面积等于黄色郁金香的面积，

则，，

，．

（2）令，则，

，，

，

易知在上单调递增，

，

答：的最大值为．

20．已知函数．

（1）证明：函数在，上单调递减；

（2）解关于的不等式；

（3）求函数的值域．

【分析】（1）解法一：直接利用导数，证明函数在，上单调递减；

解法二：利用函数单调性的定义，证明函数在，上单调递减；

（2）首先判断为奇函数，再利用函数的奇偶性、单调性，得到，由此求得的范围．

（3）根据奇函数的性质，分类讨论，再利用基本不等式，求出的值域．

【解答】解：（1）解法一：函数，，

故在，上，，当且仅当时，，

故函数在，上单调递减．

解法二：设，

则，

由题设可得，，，，即，

故函数在，上单调递减．

（2）由于满足，故为奇函数，

不等式，即不等式．

，，函数在，上单调递减，

，求得，故原不等式的解集为．

（3）当时，；

当时，，即，．

根据为奇函数，可得当时，，．

综上可得，的值域为，．

21．已知奇函数．

（1）求的值，并求函数的值域；

（2）若函数在区间，上有两个不同的零点，求的取值范围．

【分析】（1）由奇函数的性质知，求得的值；利用分离常数法，将变形为，即可求得值域；

（2）令，，原问题可转化为在，上有两个不同的零点，再根据二次函数根的分布，即可得解．

【解答】解：（1）为奇函数，且定义域为，

，解得，

，

，

，

，

故函数的值域为．

（2），

令，则，

，，，，

原问题等价于在，上有两个不同的零点，

△，解得，

当时，有，无解；

当时，有，解得，

综上所述，的取值范围为，．

22．已知命题：关于的方程有两个大于1的实数根．

（1）若命题为真命题，求实数的取值范围；

（2）命题，是否存在实数使得是的必要不充分条件，若存在，求出实数的取值范围；若不存在，说明理由．

【分析】（1）由解出两根，列出不等式组即可解出；

（2）根据充分条件，必要条件与集合包含关系等价法即可求出．

【解答】解：（1），

，解得或．依题意可得，

且，解得，故实数的取值范围为．

（2）假设存在实数使得是的必要不充分条件，所以．，

即或，解得，故实数的取值范围为，