
2022年广东省深圳市九年级数学中考二模数学试卷(四)(word版含答案)
展开2022年广东省深圳市九年级数学中考二模数学试卷(四)
一、选择题(共10小题,共30分)
1.(3分)下列计算正确的是( )
A.a2+a2=2a4 B.(a﹣1)2=a﹣2
C.(﹣2a4)4=16a8 D.a5•a2=a10
2.(3分)定义A*B、B*C、C*D、D*B,分别对应图形1、2、3、4,那么图形(1)、(2)、(3)、(4)中,可表示A*D、A*C的分别为( )
A.(1),(2) B.(2),(4) C.(2),(3) D.(1),(4)
3.(3分)如图,A,B是函数的图象上关于原点O的任意一对对称点,AC平行于y轴,BC平行于x轴,△ABC的面积为S,则( )
A.S=1 B.S=2 C.1<S<2 D.S>2
4.(3分)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为,AC=2,则sinB的值是( )
A. B. C. D.
5.(3分)小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h=3.5t﹣4.9t2(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
6.(3分)下列四种说法:
①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;
②将2020减去它的,再减去剩下的,再减去余下的,再减去余下的…依次减下去,一直到减去余下的,结果是1;
③实验的次数越多,频率越靠近理论概率;
④对于任何实数x、y,多项式x2+y2﹣4x﹣2y+7的值不小于2.其中正确的个数是( )
A.1 B.2 C.3 D.4
7.(3分)某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成,其俯视图如图所示,则此工件的左视图是( )
A. B. C. D.
8.(3分)同学们喜欢足球吗?足球一般是用黑白两种颜色的皮块缝制而成,如图所示,黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为( )
A.16块、16块 B.8块、24块 C.20块、12块 D.12块、20块
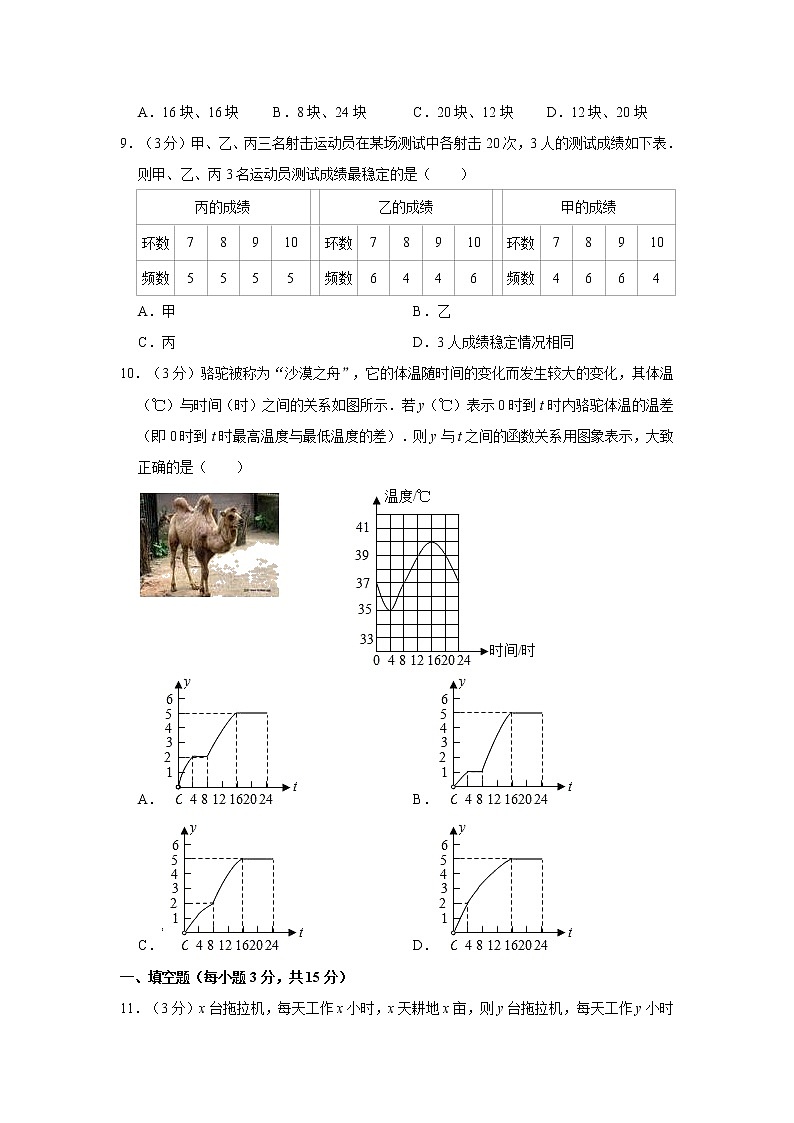
9.(3分)甲、乙、丙三名射击运动员在某场测试中各射击20次,3人的测试成绩如下表.则甲、乙、丙3名运动员测试成绩最稳定的是( )
丙的成绩
乙的成绩
甲的成绩
环数
7
8
9
10
环数
7
8
9
10
环数
7
8
9
10
频数
5
5
5
5
频数
6
4
4
6
频数
4
6
6
4
A.甲 B.乙
C.丙 D.3人成绩稳定情况相同
10.(3分)骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,其体温(℃)与时间(时)之间的关系如图所示.若y(℃)表示0时到t时内骆驼体温的温差(即0时到t时最高温度与最低温度的差).则y与t之间的函数关系用图象表示,大致正确的是( )
A. B.
C. D.
一、填空题(每小题3分,共15分)
11.(3分)x台拖拉机,每天工作x小时,x天耕地x亩,则y台拖拉机,每天工作y小时,y天耕地 亩.
12.(3分)将一块弧长为2π的半圆形铁皮围成一个圆锥的侧面(接头忽略不计),则围成的圆锥的高为 .
13.(3分)一颗参天大树,树干周长为3米,地上有一根常青藤恰好绕了它5圈,藤尖离地面20米高.那么,这根常青藤至少有 米.
14.(3分)如图,△ADC中,AD=AC,延长CD至B,使BD=CD,ED⊥BC交AB于E,EC交AD于F,下列四个结论:
①EB=EC:
②BC=2AD;
③△ABC∽△FCD;
④若AC=6,则DF=3.
其中正确的是
15.(3分)已知方程2x2+kx﹣2k+1=0的两个实数根的平方和为,则k的值为 .
二、解答题(共7小题,共55分)
16.(6分)当x=+1,求(x﹣)÷(1+)的值.
17.(6分)将A,B,C,D四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
(1)A在甲组的概率是多少?
(2)A,B都在甲组的概率是多少?
18.(7分)一次函数y=k1x+b和反比例函数y=的图象相交于点P(m﹣1,n+1),点Q(0,a)在函数y=k1x+b的图象上,且m,n是关于x的方程ax2﹣(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),求一次函数和反比例函数的解析式.
19.(8分)节日里,姐妹两人在50米的跑道上进行短路比赛,两人从出发点同时起跑,姐姐到达终点时,妹妹离终点还差3米,已知姐妹两人的平均速度分别为a米/秒、b米/秒.
(1)如果两人重新开始比赛,姐姐从起点向后退3米,姐妹同时起跑,两人能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)如果两人想同时到达终点,应如何安排两人的起跑位置?请你设计两种方案.
20.(8分)如图,AB是半圆O的直径,AD为弦,∠DBC=∠A.
(1)求证:BC是半圆O的切线;
(2)若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
21.(10分)某环保器材公司销售一种市场需求较大的新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售该种产品的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
(1)求y关于x的函数关系式;
(2)写出该公司销售该种产品年获利w(万元)关于销售单价x(元)的函数关系式;(年获利=年销售总金额一年销售产品的总进价一年总开支金额)当销售单价x为何值时,年获利最大?最大值是多少?
(3)若公司希望该产品一年的销售获利不低于57.5万元,请你利用(2)小题中的函数图象帮助该公司确定这种产品的销售单价的范围.在此条件下要使产品的销售量最大,你认为销售单价应定为多少元?
22.(10分)如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.
2022年广东省深圳市九年级数学中考二模数学试卷(四)
参考答案与试题解析
一、选择题(共10小题,共30分)
1.(3分)下列计算正确的是( )
A.a2+a2=2a4 B.(a﹣1)2=a﹣2
C.(﹣2a4)4=16a8 D.a5•a2=a10
【分析】分别根据合并同类项法则,幂的乘方运算法则,积的乘方运算法则以及同底数幂的乘法法则逐一判断即可.
【解答】解:A.a2+a2=2a2,故本选项不合题意;
B.(a﹣1)2=a﹣2,故本选项符合题意;
C.(﹣2a4)4=16a16,故本选项不合题意;
D.a5•a2=a7,故本选项不合题意.
故选:B.
2.(3分)定义A*B、B*C、C*D、D*B,分别对应图形1、2、3、4,那么图形(1)、(2)、(3)、(4)中,可表示A*D、A*C的分别为( )
A.(1),(2) B.(2),(4) C.(2),(3) D.(1),(4)
【分析】观察发现,“*”表示两种几何图形的复合,根据已知定义判断出A、B、C、D分别表示的图形,然后代入A*D、A*C即可求解.
【解答】解:运算“*”表示两种几何图形的复合图形,
∵由1、2可得B是公共图形,
∴B表示大方框,
∵由2、3可得C是公共图形,
∴C表示横线,
∴A表示竖线,D表示小方框,
∴A*D表示竖线与小方框组成的图形,A*C表示竖线与横线组成的图形,
故A*D、A*C的分别为(2),(4).
故选:B.
3.(3分)如图,A,B是函数的图象上关于原点O的任意一对对称点,AC平行于y轴,BC平行于x轴,△ABC的面积为S,则( )
A.S=1 B.S=2 C.1<S<2 D.S>2
【分析】设出点A的坐标,可得点B的坐标.易得△ABC为直角三角形,面积等于×AC×BC,把相关数值代入求值即可.
【解答】解:设点A的坐标为(x,y),点A在反比例函数解析式上,
∴点B的坐标为(﹣x,﹣y),k=xy=1
∵AC平行于y轴,BC平行于x轴,
∴△ABC的直角三角形,
∴AC=2y,BC=2x,
∴S=×2y×2x=2xy=2.
故选:B.
4.(3分)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为,AC=2,则sinB的值是( )
A. B. C. D.
【分析】求角的三角函数值,可以转化为求直角三角形边的比,连接DC.根据同弧所对的圆周角相等,就可以转化为:求直角三角形的锐角的三角函数值的问题.
【解答】解:连接DC.
根据直径所对的圆周角是直角,得∠ACD=90°.
根据同弧所对的圆周角相等,得∠B=∠D.
∴sinB=sinD==.
故选:A.
5.(3分)小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h=3.5t﹣4.9t2(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
【分析】找重心最高点,就是要求这个二次函数的顶点,应该把一般式化成顶点式后,直接解答.
【解答】解:
h=3.5t﹣4.9t2
=﹣4.9(t﹣)2+,
∵﹣4.9<0
∴当t=≈0.36s时,h最大.
故选:D.
6.(3分)下列四种说法:
①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;
②将2020减去它的,再减去剩下的,再减去余下的,再减去余下的…依次减下去,一直到减去余下的,结果是1;
③实验的次数越多,频率越靠近理论概率;
④对于任何实数x、y,多项式x2+y2﹣4x﹣2y+7的值不小于2.其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】①根据平行线的性质即可判断;
②根据题意列出算式,进行化简计算即可;
③利用频率估计概率的方法即可判断;
④根据配方法先将多项式进行配方,再利用非负数的性质进行计算即可.
【解答】解:①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,故①错误;
②将2020减去它的,再减去剩下的,再减去余下的,再减去余下的…依次减下去,一直到减去余下的,结果是1,正确,
∵2020×(1﹣)×(1﹣)×(1﹣)×…×(1﹣)
=2020××××…××
=2020×
=1.
故②正确;
③实验的次数越多,频率越靠近理论概率,故③正确;
④对于任何实数x、y,多项式x2+y2﹣4x﹣2y+7的值不小于2,正确,
∵x2+y2﹣4x﹣2y+7
=x2﹣4x+4+y2﹣2y+1+2
=(x﹣2)2+(y﹣1)2+2,
∵(x﹣2)2≥0,(y﹣1)2≥0,
∴(x﹣2)2+(y﹣1)2+2≥2,
故④正确.
其中正确的个数是3.
故选:C.
7.(3分)某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成,其俯视图如图所示,则此工件的左视图是( )
A. B. C. D.
【分析】找到从正面看所得到的图形即可,注意看到的用实线表示,看不到的用虚线表示.
【解答】解:从左面看应是一长方形,看不到的应用虚线,由俯视图可知,虚线离边较近.
故选:A.
8.(3分)同学们喜欢足球吗?足球一般是用黑白两种颜色的皮块缝制而成,如图所示,黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为( )
A.16块、16块 B.8块、24块 C.20块、12块 D.12块、20块
【分析】根据题意可知:本题中的等量关系是“黑白皮块32块”和因为每块白皮有3条边与黑边连在一起,所以与黑皮重合的边有3y,而黑皮共有边数为5x,依此列方程组求解即可.
【解答】解:设黑色皮块和白色皮块的块数依次为x,y.
则,
解得,
即黑色皮块和白色皮块的块数依次为12块、20块.
故选:D.
9.(3分)甲、乙、丙三名射击运动员在某场测试中各射击20次,3人的测试成绩如下表.则甲、乙、丙3名运动员测试成绩最稳定的是( )
丙的成绩
乙的成绩
甲的成绩
环数
7
8
9
10
环数
7
8
9
10
环数
7
8
9
10
频数
5
5
5
5
频数
6
4
4
6
频数
4
6
6
4
A.甲 B.乙
C.丙 D.3人成绩稳定情况相同
【分析】根据题意,分别计算甲乙丙三个人的方差可得,甲的方差小于乙、丙的方差,结合方差的意义,可得甲最稳定.
【解答】解:甲的平均数=(7×4+8×6+9×6+10×4)÷20=8.5
乙的平均数=(7×6+8×4+9×4+10×6)÷20=8.5
丙的平均数=(7×5+8×5+9×5+10×5)÷20=8.5
S甲2=[4×(7﹣8.5)2+6×(8﹣8.5)2+6×(9﹣8.5)2+4×(10﹣8.5)2]÷20=1.05
S乙2=[4×(8﹣8.5)2+6×(7﹣8.5)2+6×(10﹣8.5)2+4×(9﹣8.5)2]÷20=1.45
S丙2=[5×(7﹣8.5)2+5×(8﹣8.5)2+5×(9﹣8.5)2+5×(10﹣8.5)2]÷20=1.25
∵S甲2<S丙2<S乙2
∴甲的成绩最稳定.
故选:A.
10.(3分)骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,其体温(℃)与时间(时)之间的关系如图所示.若y(℃)表示0时到t时内骆驼体温的温差(即0时到t时最高温度与最低温度的差).则y与t之间的函数关系用图象表示,大致正确的是( )
A. B.
C. D.
【分析】根据时间和体温的变化,将时间分为3段:0﹣4,4﹣8,8﹣16,16﹣24,分别观察每段中的温差,由此即可求出答案.
【解答】解:从0时到4时,温差随时间的增大而增大,在4时达到最大,是2℃;再到8时,这段时间的最高温度是37℃,最低是35℃,温差不变,由此可以排除C、D,从8时开始,最高温度变大,最低温度不变是35℃,温差变大,达到3℃,从16时开始体温下降,温差不变.
故选:A.
二、填空题(每小题3分,共15分)
11.(3分)x台拖拉机,每天工作x小时,x天耕地x亩,则y台拖拉机,每天工作y小时,y天耕地 亩.
【分析】根据题意,可以表示出每亩地需要的时间,然后即可得到y台拖拉机,每天工作y小时,y天耕地多少亩.
【解答】解:由题意可得,
每亩地需要的时间为:=x2,
则y台拖拉机,每天工作y小时,y天耕地:=,
故答案为:.
12.(3分)将一块弧长为2π的半圆形铁皮围成一个圆锥的侧面(接头忽略不计),则围成的圆锥的高为 .
【分析】根据弧长公式计算出半径和母线长,然后运用勾股定理求出圆锥的高.
【解答】解:∵l==2π,
∴母线长为R=2,
又∵2π=2πr,
∴r=1,
设高为H,则H,R,r构成以R为斜边的直角三角形,
所以H==.
故答案为:.
13.(3分)一颗参天大树,树干周长为3米,地上有一根常青藤恰好绕了它5圈,藤尖离地面20米高.那么,这根常青藤至少有 25 米.
【分析】根据勾股定理即可得到结论.
【解答】解:根据题意得,这根常青藤至少有=25(米),
故答案为:25米.
14.(3分)如图,△ADC中,AD=AC,延长CD至B,使BD=CD,ED⊥BC交AB于E,EC交AD于F,下列四个结论:
①EB=EC:
②BC=2AD;
③△ABC∽△FCD;
④若AC=6,则DF=3.
其中正确的是①③④
【分析】根据线段垂直平分线的性质得到BE=CE,BC=2BD=2CD,故①正确;②错误;根据等腰三角形的性质得到∠ADC=∠ACB,推出△ABC∽△FCD;故③正确;根据相似三角形的性质得到=,得到DF=3,故④正确.
【解答】解:∵BD=CD,ED⊥BC,
∴BE=CE,BC=2BD=2CD,故①正确;②错误;
∵AD=AC,
∴∠ADC=∠ACB,
∵∠B=∠ECB,
∴△ABC∽△FCD;故③正确;
∴=,
∵BC=2CD,
∴AD=AC=2FD=6,
∴DF=3,故④正确;
故答案是:①③④ .
15.(3分)已知方程2x2+kx﹣2k+1=0的两个实数根的平方和为,则k的值为 3 .
【分析】根据根与系数的关系求得x1+x2=﹣,x1•x2=﹣k+;然后将其代入x12+x22=(x1+x2)2﹣4x1x2列出关于k的新方程,通过解新方程即可求得k的值.
【解答】解:∵方程2x2+kx﹣2k+1=0有两个实数根,
∴△=k2﹣4×2(﹣2k+1)≥0,
解得k≥6﹣8或k≤﹣6﹣8.
设方程2x2+kx﹣2k+1=0两个实数根为x1、x2.则
x1+x2=﹣,x1•x2=﹣k+,
∴x12+x22=(x1+x2)2﹣2x1x2=+2k﹣1=,即k2+8k﹣33=0,
解得k1=3,k2=﹣11(不合题意,舍去).
故答案是:3.
三、解答题(共7小题,共55分)
16.(6分)当x=+1,求(x﹣)÷(1+)的值.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x的值化简、代入计算可得.
【解答】解:原式=(﹣)÷(+)
=•
=x﹣1,
当x=+1=2+1时,
原式=2+1﹣1=2.
17.(6分)将A,B,C,D四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
(1)A在甲组的概率是多少?
(2)A,B都在甲组的概率是多少?
【分析】列举出符合题意的各种情况的个数,再根据概率公式解答即可.
【解答】解:所有可能出现的结果如下:
甲组
乙组
结果
AB
CD
(AB,CD)
AC
BD
(AC,BD)
AD
BC
(AD,BC)
BC
AD
(BC,AD)
BD
A C
(BD,AC)
CD
AB
(CD,AB)
总共有6种结果,每种结果出现的可能性相同.
(1)所有的结果中,满足A在甲组的结果有3种,所以A在甲组的概率是.(2分)
(2)所有的结果中,满足A,B都在甲组的结果有1种,所以A,B都在甲组的概率是.(6分)
18.(7分)一次函数y=k1x+b和反比例函数y=的图象相交于点P(m﹣1,n+1),点Q(0,a)在函数y=k1x+b的图象上,且m,n是关于x的方程ax2﹣(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),求一次函数和反比例函数的解析式.
【分析】m,n是关于x的方程ax2﹣(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),得出a=﹣1,m=2,n=0,或m=0,n=2,从而求得P、Q的坐标,根据待定系数法即可求得一次函数和反比例函数的解析式.
【解答】解:解方程ax2﹣(3a+1)x+2(a+1)=0,
得:x=2,x=
∵m,n是关于x的方程ax2﹣(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),
∴a=﹣1,
∴x1=2,x2=0,
∴m=2,n=0,或m=0,n=2,
∴P(1,1),或P(﹣1,3),Q(0,﹣1),
把P,Q的坐标代入y=k1x+b得或,
解得或,
∴一次函数的解析式为y=2x﹣1或y=﹣4x﹣1;
把P的坐标代入y=得k2=1或﹣3,
∴反比例函数的解析式y=或y=﹣.
19.(8分)节日里,姐妹两人在50米的跑道上进行短路比赛,两人从出发点同时起跑,姐姐到达终点时,妹妹离终点还差3米,已知姐妹两人的平均速度分别为a米/秒、b米/秒.
(1)如果两人重新开始比赛,姐姐从起点向后退3米,姐妹同时起跑,两人能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)如果两人想同时到达终点,应如何安排两人的起跑位置?请你设计两种方案.
【分析】(1)姐妹两人在相同时间内所走的路程之比为:50:47,可得两人的速度之比为50:47,设出其中一人的速度,得到另一人的速度,分别算出两人到底终点的时间,比较即可得到谁先到达终点;
(2)①若妹妹在起跑线不动,表示出同时到终点所用时间,所以姐姐应该后退的米数为姐姐的速度乘以到达的时间数﹣50;
②同理,若姐姐在起跑线不动,则妹妹只需向前3米,便可与姐姐同时到达终点.
【解答】解:(1)姐妹两人在相同时间内所走的路程之比为:50:47,可得两人的速度之比为50:47,设姐姐的速度为50k米/秒,则妹妹的速度为47k米/秒,
姐姐所用的时间为:秒,
妹妹所用的时间为:秒,
﹣==<0,
∴姐姐先到;
(2)若安排姐姐后退,则两人同时到达的时间为妹妹跑50米用的时间为,此时姐姐跑的米数为:×50k=米,
后退的米数为:﹣50=米;
若安排妹妹前进,则两人同时到达的时间为姐姐跑50米用的时间为=,此时妹妹跑的米数为:×47k=47m,需前进的米数为50﹣47=3米;
答:姐姐后退米或妹妹前进3米.
20.(8分)如图,AB是半圆O的直径,AD为弦,∠DBC=∠A.
(1)求证:BC是半圆O的切线;
(2)若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
【分析】(1)若证明BC是半圆O的切线,利用切线的判定定理:即证明AB⊥BC即可;
(2)因为OC∥AD,可得∠BEC=∠D=90°,再有其他条件可判定△BCE∽△BAD,利用相似三角形的性质:对应边的比值相等即可求出AD的长.
【解答】(1)证明:∵AB是半圆O的直径,
∴BD⊥AD,
∴∠DBA+∠A=90°,
∵∠DBC=∠A,
∴∠DBA+∠DBC=90°即AB⊥BC,
∴BC是半圆O的切线;
(2)解:∵OC∥AD,
∴∠BEC=∠D=90°,
∵BD⊥AD,BD=6,
∴BE=DE=3,
∵∠DBC=∠A,
∴△BCE∽△BAD,
∴,即,
∴AD=4.5
21.(10分)某环保器材公司销售一种市场需求较大的新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售该种产品的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
(1)求y关于x的函数关系式;
(2)写出该公司销售该种产品年获利w(万元)关于销售单价x(元)的函数关系式;(年获利=年销售总金额一年销售产品的总进价一年总开支金额)当销售单价x为何值时,年获利最大?最大值是多少?
(3)若公司希望该产品一年的销售获利不低于57.5万元,请你利用(2)小题中的函数图象帮助该公司确定这种产品的销售单价的范围.在此条件下要使产品的销售量最大,你认为销售单价应定为多少元?
【分析】(1)由图象可知y关于x的函数关系式是一次函数,设y=kx+b,用“两点法”可求解析式;
(2)根据年获利=年销售总金额一年销售产品的总进价一年总开支金额,列出函数关系式;
(3)求出年销售获利等于57.5万元时,销售单价x的值,从而确定销售单价x的范围,及二次函数w最大时,x的值.
【解答】解:(1)由题意,设y=kx+b,图象过点(70,5),(90,3),
∴
解得
∴y=﹣x+12.
(2)由题意,得
w=y(x﹣40)﹣z
=y(x﹣40)﹣(10y+42.5)
=(x+12)(x﹣40)﹣10(x+12)﹣42.5
=﹣0.1x2+17x﹣642.5=(x﹣85)2+80.
当x=85元时,年获利的最大值为80万元.
(3)令w=57.5,得﹣0.1x2+17x﹣642.5=57.5.
整理,得x2﹣170x+7000=0.
解得x1=70,x2=100.
由图象可知,要使年获利不低于57.5万元,销售单价应在70元到100元之间.
又因为销售单价越低,销售量越大,
所以要使销售量最大,又使年获利不低于57.5万元,销售单价应定为70元.
22.(10分)如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.
【分析】(1)根据已知,由直角三角形的性质可知AB=2,从而求得AD,CD,利用中位线的性质可得EF,DF,利用三角函数可得GF,由矩形的面积公式可得结果;
(2)首先利用分类讨论的思想,分析当矩形与△CBD重叠部分为三角形时(),利用三角函数和三角形的面积公式可得结果;当矩形与△CBD重叠部分为直角梯形时(),列出方程解得x;
(3)作H2Q⊥AB于Q,设DQ=m,则,又DG1=,,利用勾股定理可得m,在Rt△QH2G1中,利用三角函数解得cosα.
【解答】解:(1)如图①,在△ABC中,
∵∠ACB=90°,∠B=30°,AC=1,
∴AB=2,
又∵D是AB的中点,
∴AD=1,,
又∵EF是△ACD的中位线,
∴,
在△ACD中,AD=CD,∠A=60°,
∴∠ADC=60°,
在△FGD中,GF=DF•sin60°=,
∴矩形EFGH的面积;
(2)如图②,设矩形移动的距离为x,则,
当矩形与△CBD重叠部分为三角形时,
则,,
∴.(舍去),
当矩形与△CBD重叠部分为直角梯形时,则,
重叠部分的面积S=,
∴,
即矩形移动的距离为时,矩形与△CBD重叠部分的面积是;
(3)如图③,作H2Q⊥AB于Q,
设DQ=m,则,又DG1=,.
在Rt△H2QG1中,(m)2+(m+)2=()2,
解之得:m1=,m2=(负的舍去).
∴cosα===.
2022年广东省深圳市深圳中学中考数学一模试卷(word版含答案): 这是一份2022年广东省深圳市深圳中学中考数学一模试卷(word版含答案),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年广东省深圳市坪山区中考数学一模试题(word版含答案): 这是一份2022年广东省深圳市坪山区中考数学一模试题(word版含答案),共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2021年广东省深圳市九年级中考二模数学试卷(word版含答案): 这是一份2021年广东省深圳市九年级中考二模数学试卷(word版含答案),共25页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












