



- 专题10.12第10章分式单元测试(培优卷)-2021-2022学年八年级数学下册尖子生同步培优题典【苏科版】 试卷 6 次下载
- 专题11.1反比例函数-2021-2022学年八年级数学下册尖子生同步培优题典【苏科版】 试卷 3 次下载
- 专题11.3用反比例函数解决问题-2021-2022学年八年级数学下册尖子生同步培优题典【苏科版】 试卷 4 次下载
- 专题11.4反比例函数的k值问题(重难点培优)-2021-2022学年八年级数学下册尖子生同步培优题典【苏科版】 试卷 8 次下载
- 专题11.5反比例函数与一次函数(重难点培优)-2021-2022学年八年级数学下册尖子生同步培优题典【苏科版】 试卷 9 次下载
数学苏科版11.2 反比例函数的图象与性质课时作业
展开2021-2022学年八年级数学下册尖子生同步培优题典【苏科版】
专题11.2反比例函数的图象与性质
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋•兰州期末)在反比例函数y=1−2mx,图象分布在一三象限,则m的取值范围是( )
A.m<0 B.m>0 C.m<12 D.m>12
【分析】根据反比例函数图象所在象限可得1﹣2m>0,再解即可.
【解析】∵反比例函数y=1−2mx,图象分布在一三象限,
∴1﹣2m>0,
解得:m<12,
故选:C.
2.(2020秋•如皋市期中)如图,在平面直角坐标系中,函数y=3x(x>0)与y=x﹣1的图象交于点P(a,b),则代数式1a−1b的值为( )
A.−14 B.14 C.−13 D.13
【分析】由题意得,函数y=3x(x>0)与y=x﹣1的图象交于点P(a,b),则ab=3,b=a﹣1,进而求解.
【解答】由题意得,函数y=3x(x>0)与y=x﹣1的图象交于点P(a,b),
∴ab=3,b=a﹣1,
∴1a−1b=b−aab=−13;
故选:C.
3.(2020春•工业园区校级期中)反比例函数y=1−mx的图象在第一、第三象限,则m可能取的一个值为( )
A.0 B.1 C.2 D.3
【分析】根据反比例函数的性质可知,当函数图象在第一、第三象限,则反比例函数的系数大于0,据此列不等式解答即可.
【解析】∵反比例函数y=1−mx的图象在第一、第三象限,
∴1﹣m>0,
∴m<1,
符合条件的答案只有A,
故选:A.
4.(2020春•亭湖区校级月考)如图,已知点P在反比例函数y=kx的图象上,PA⊥x轴,垂足为点A.且△AOP的面积为2,则k的值为( )
A.4 B.﹣4 C.2 D.﹣2
【分析】根据反比例函数k的几何意义,可得12|k|=2,再根据k<0,求出k的值.
【解析】∵点P在反比例函数y=kx的图象上,PA⊥x轴,且△AOP的面积为2,
∴12|k|=2,
∵k<0,
∴k=﹣4.
故选:B.
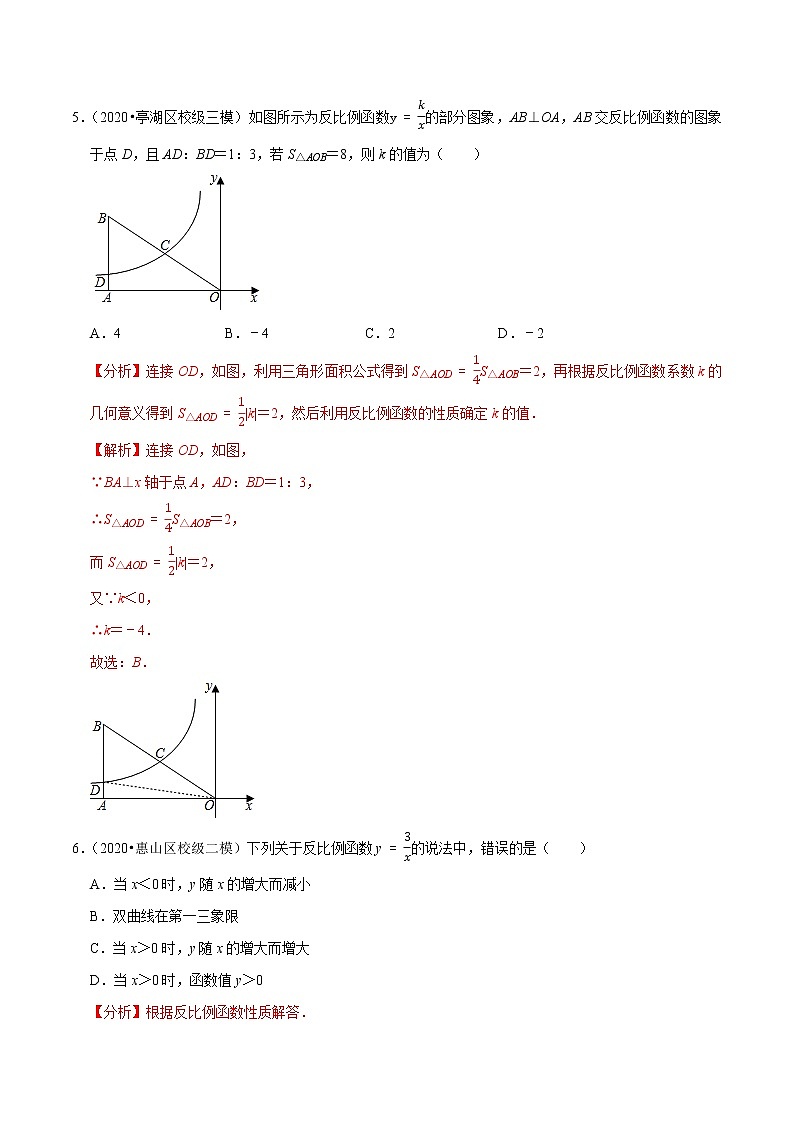
5.(2020•亭湖区校级三模)如图所示为反比例函数y=kx的部分图象,AB⊥OA,AB交反比例函数的图象于点D,且AD:BD=1:3,若S△AOB=8,则k的值为( )
A.4 B.﹣4 C.2 D.﹣2
【分析】连接OD,如图,利用三角形面积公式得到S△AOD=14S△AOB=2,再根据反比例函数系数k的几何意义得到S△AOD=12|k|=2,然后利用反比例函数的性质确定k的值.
【解析】连接OD,如图,
∵BA⊥x轴于点A,AD:BD=1:3,
∴S△AOD=14S△AOB=2,
而S△AOD=12|k|=2,
又∵k<0,
∴k=﹣4.
故选:B.
6.(2020•惠山区校级二模)下列关于反比例函数y=3x的说法中,错误的是( )
A.当x<0时,y随x的增大而减小
B.双曲线在第一三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,函数值y>0
【分析】根据反比例函数性质解答.
【解析】∵反比例函数y=3x中,k=3>0,
∴双曲线在第一、三象限,在每个象限内,y随x的增大而减小,
∴A、B、D正确,C错误;
故选:C.
7.(2020•射阳县二模)如图,矩形OABC的一个顶点与坐标原点重合,OC、OA分别在x轴和y轴上,正方形CDEF的一条边在x轴上,另一条边CD在BC上,反比例函数y=−20x的图象经过B、E两点,已知OA=5,则正方形的边长是( )
A.46−2 B.4﹣26 C.26−2 D.6
【分析】先求出点B坐标,设正方形的边长为a,可得点E(﹣4﹣a,a),代入解析式可求解.
【解析】∵OA=5,
∴点B的纵坐标为5,
∵点B在反比例函数图象上,
∴5=−20x,
∴x=﹣4,
∴点B(﹣4,5),
设正方形的边长为a,
∴点E(﹣4﹣a,a),
∵点E在反比例函数y=−20x的图象上,
∴(﹣4﹣a)a=﹣20,
∴a=26−2,(负值舍去),
故选:C.
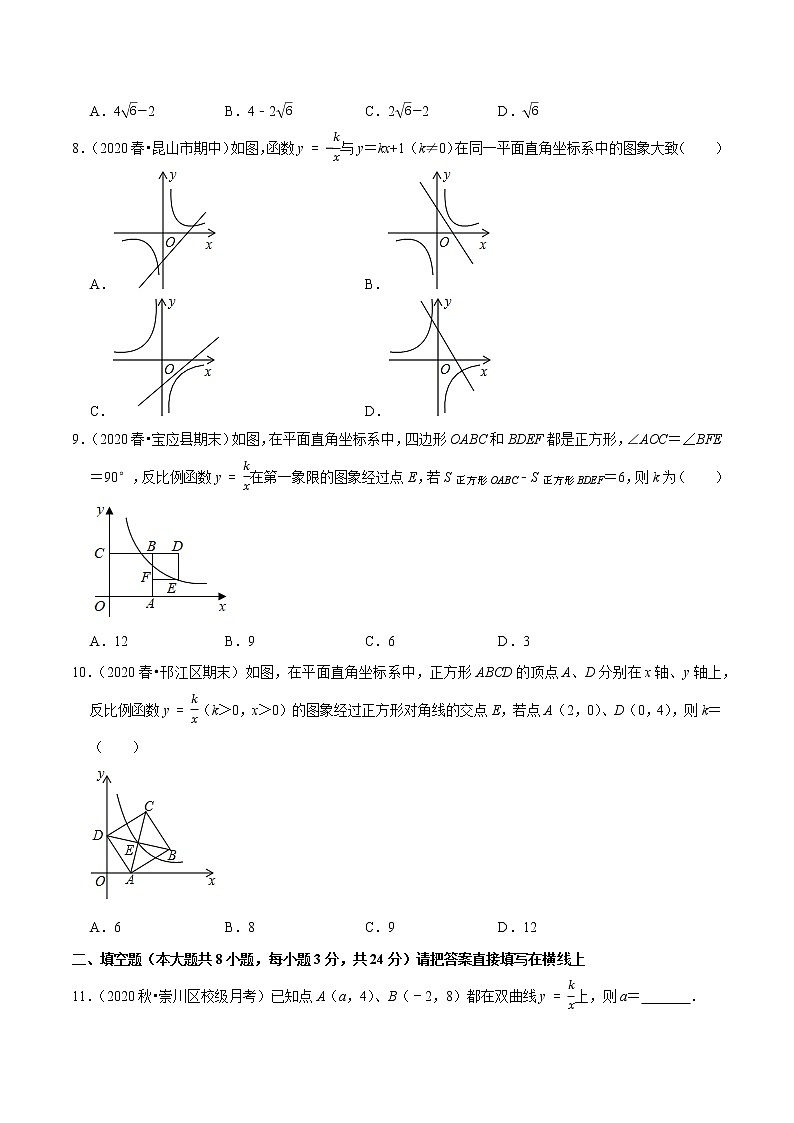
8.(2020春•昆山市期中)如图,函数y=−kx与y=kx+1(k≠0)在同一平面直角坐标系中的图象大致( )
A. B.
C. D.
【分析】比例系数相同,两个函数必有交点,然后根据比例系数的符号确定正确选项即可.
【解析】k>0时,一次函数y=kx+1的图象经过第一、二、三象限,反比例函数的两个分支分别位于第二、四象限;
当k<0时,函数y=kx+1的图象经过一、二、四象限,反比例函数的图象分布在一、三象限,B选项正确,
故选:B.
9.(2020春•宝应县期末)如图,在平面直角坐标系中,四边形OABC和BDEF都是正方形,∠AOC=∠BFE=90°,反比例函数y=kx在第一象限的图象经过点E,若S正方形OABC﹣S正方形BDEF=6,则k为( )
A.12 B.9 C.6 D.3
【分析】设正方形OABC、BDEF的边长分别为a和b,则可表示出D(a+b,a),E(a+b,a﹣b),则a2﹣b2=k,然后利用正方形的面积公式易得k=6.
【解析】设正方形OABC、BDEF的边长分别为a和b,则D(a+b,a),E(a+b,a﹣b),
∵点E在反比例函数上,
∴(a+b)(a﹣b)=k,
∴a2﹣b2=k,
∵S正方形OABC﹣S正方形BDEF=a2﹣b2=6,
∴k=6
故选:C.
10.(2020春•邗江区期末)如图,在平面直角坐标系中,正方形ABCD的顶点A、D分别在x轴、y轴上,反比例函数y=kx(k>0,x>0)的图象经过正方形对角线的交点E,若点A(2,0)、D(0,4),则k=( )
A.6 B.8 C.9 D.12
【分析】通过证得△AOD≌△BMA求出B的坐标,进而得到E点坐标,代入y=kx,利用待定系数法求出k.
【解析】作BM⊥x轴于M,
由正方形的性质可知AD=AB,∠BAD=90°,BE=DE,
∴∠ADO+∠DAO=∠DAO+∠BAM,
∴∠ADO=∠BAM,
∵∠AOD=∠BMA=90°,
∴△AOD≌△BMA(AAS),
∴OA=BM,OD=AM,
∵点A(2,0)、D(0,4),
∴OA=2,OD=4,
∴BM=OA=2,OM=2+4=6,
∴B(6,2),
∵E是BD的中点,
∴E(3,3),
∵反比例函数y=kx(k>0,x>0)的图象经过点E,
∴k=3×3=9.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋•崇川区校级月考)已知点A(a,4)、B(﹣2,8)都在双曲线y=kx上,则a= ﹣4 .
【分析】将点A坐标,点B坐标代入解析式可求a的值.
【解析】∵点A(a,4)、B(﹣2,8)都在双曲线y=kx上,
∴k=4a=﹣2×8,
∴a=﹣4,
故答案为:﹣4.
12.(2020春•工业园区校级期中)点P(m,n)是函数y=−3x和y=x+4图象的一个交点,则mn+n﹣m的值为 1 .
【分析】把P的坐标分别代入两个解析式即可得到mn=﹣3,n﹣m=4,代入代数式 求得即可.
【解析】∵点P(m,n)是函数y=−3x和y=x+4图象的一个交点,
∴mn=﹣3,n=m+4,
∴n﹣m=4,
∴mn+n﹣m=﹣3+4=1,
故答案为1.
13.(2020•建邺区二模)在同一平面直角坐标系中,正比例函数y=k1x的图象与反比例函数y=k2x的图象一个交点的坐标是(﹣1,3),则它们另一个交点的坐标是 (1,﹣3) .
【分析】反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称.
【解析】根据题意,直线y=k1x经过原点与双曲线y=k2x相交于两点,
又由于双曲线y=k2x与直线y=k1x均关于原点对称.
则两点关于原点对称,一个交点的坐标为(﹣1,3),
则另一个交点的坐标为(1,﹣3).
故答案为:(1,﹣3).
14.(2020秋•崇川区校级月考)在平面直角坐标系中,等边△ABC如图放置,其中B(2,0),则过点A的反比例函数的表达式为 y=3x .
【分析】作AC⊥OB,根据等边三角形的性质、正弦和余弦的定义分别求出OC、AC,利用待定系数法求出反比例函数解析式.
【解析】过点A作AC⊥OB于C,
设过点A的反比例函数的表达式为y=kx,
∵△OAB是等边三角形,
∴OA=2,∠AOC=60°,
∴OC=OA×cos∠AOC=2×12=1,AC=OA×sin∠AOC=2×32=3,
∴点A的坐标为(1,3),
∴3=k1,
解得,k=3,
∴过点A的反比例函数的表达式为y=3x,
故答案为:y=3x.
15.(2020春•海陵区校级期中)双曲线y=kx经过点A(a,﹣2a),B(﹣2,m),C(﹣3,n),则m > n(>,=,<).
【分析】先求得双曲线所处的象限,然后根据反比例函数的性质即可求得.
【解析】∵双曲线y=kx经过点A(a,﹣2a),
∴k=﹣2a2<0,
∴双曲线在二、四象限,在每个象限内,y随x的增大而增大,
∵B(﹣2,m),C(﹣3,n),﹣2>﹣3,
∴m>n,
故答案为>.
16.(2020春•相城区期中)在反比例函数y=−k2+1x图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则y1、y2、y3的大小关系为 y2<y3<y1 .(用“<”连接)
【分析】根据反比例函数的性质得到反比例函数图象分布在第二、四象限,然后利用x1<0<x2<x3得到y1>0,y2<y3<0.
【解析】∵﹣(k2+1)<0,
∴反比例函数图象分布在第二、四象限,
∵x1<0<x2<x3,
∴y1>0,y2<y3<0,
∴y2<y3<y1.
故答案为y2<y3<y1.
17.(2020•东台市模拟)如图,已知点A是反比例函数y=−4x图象上的一个动点,连接OA,若将线段OA绕点O逆时针旋转90°得到线段OB,则过点B的反比例函数解析式为 y=4x .
【分析】设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,得到AC=n,OC=﹣m,根据全等三角形的性质得到AC=OD=n,CO=BD=﹣m,于是得到结论.
【解析】设A(m,n),
∵点A是反比例函数y=−4x图象上的一个动点,
∴mn=﹣4,
过A作AC⊥x轴于C,过B作BD⊥x轴于D,
∴AC=n,OC=﹣m,
∴∠ACO=∠BDO=90°,
∵∠AOB=90°,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
在△ACO与△ODB中,
∠ACO=∠ODB∠CAO=∠BODAO=BO,
∴△ACO≌△ODB(AAS),
∴AC=OD=n,CO=BD=﹣m,
∴B(﹣n,m),
∵mn=﹣4,
∴﹣nm=4,
∴点B所在图象的函数表达式为y=4x,
故答案为:y=4x.
18.(2020•滨湖区模拟)如图,已知平面直角坐标系中A点坐标为(0,3),以OA为一边在第一象限作三角形OAB.E为AB中点,OB=4.若反比例函数y=kx的图象恰好经过点B和点E,则k的值为 15 .
【分析】分别按照点E在反比例函数图象上和作为线段AB的中点,用两种方式表示出点E的纵坐标,从而得到关于x和k的等式,解得x和k的关系,然后根据勾股定理得关于k的方程,解得k的值,舍去负值,即可得出答案.
【解析】∵反比例函数y=kx的图象恰好经过点B和点E,E为AB中点,
∴设B(x,kx),则点E(x2,2kx),
∵A(0,3)E为AB中点,
∴点E的坐标又可以表示为:(x2,kx+32),
∴2kx=k2x+32,
解得:kx=1,
∴x=k,
∴B(k,1)
∵OB=4,
∴k2+12=42,
∴k=±15,
∵k>0,
∴k=15,
故答案为15.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春•张家港市期末)已知反比例函数y=−3x的图象经过点A(﹣2,m).
(1)求m的值;
(2)若点B(x1,y1),C(x2,y2)是该反比例函数图象上的两点,并且满足x1>x2>0,则y1与y2的大小关系是 y2<y1 (用“<”号连接).
【分析】(1)把点A(﹣2,m)代入y=−3x即可求得.
(2)根据反比例函数y=−3x,判断此函数图象所在的象限,再根据x1>x2>0判断出B(x1,y1)、C(x2,y2)所在的象限,根据此函数的增减性即可解答.
【解析】(1)∵反比例函数y=−3x的图象经过点A(﹣2,m).
∴m=−3−2=32;
(2)反比例函数y=−3x中,k=﹣3<0,
∴此函数的图象在二、四象限,在每一象限内y随x的增大而增大,
∵x1>x2>0,
∴B(x1,y1)、C(x2,y2)两点均位于第四象限,
∴y2<y1.
故答案为:y2<y1.
20.(2020春•宝应县期末)如图,一次函数y=x+m的图象与反比例函数y=kx的图象交于A、B两点,点A的坐标为(1,2).
(1)求m、k的值;
(2)求点B的坐标,并结合图象写出不等式x+m−kx<0的解集?
【分析】(1)用待定系数法即可求解;
(2)联立①②并整理得:x2+x﹣2=0,解得:x=2或1,通过观察图象即可求解.
【解析】(1)将点A的坐标代入反比例函数表达式得:2=k1,
解得:k=2,
故反比例函数的表达式为y=2x①,
将点A的坐标代入一次函数表达式得:1+m=2,解得:m=1,
故一次函数的表达式为y=x+1②,
即k=2,m=1;
(2)联立①②并整理得:x2+x﹣2=0,解得:x=2或1,
即点B的坐标为(﹣2,﹣1),
由图象知,x+m−kx<0的解集为x<﹣2或0<x<1.
21.(2020春•扬中市期末)如图,在平面直角坐标系中,点A(3,2)在反比例函数y=kx(x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.
(1)求该反比例函数的解析式;
(2)当点B(6,4)时,求S△ABD;
(3)若S△ACD=52,则线段BD= 353 .
【分析】(1)把点A(3,2)代入反比例函数的解析式y=kx,即可求出函数解析式;
(2)由B的坐标和反比例函数解析式求得D点的坐标,进而求得BD,根据三角形的面积公式即可求得结论;
(3)直线OA的关系式可求,由于点C(a,0),可以表示点B、D的坐标,根据S△ACD=52,建立方程可以解出a的值;
根据求得a的值可以求出BD的长.
【解析】(1)∵点A(3,2)在反比例函数y=kx(x>0)的图象上,
∴k=3×2=6,
∴反比例函数的解析式为y=6x;
(2)∵点B(6,4),
∴D点的横坐标是6,
∵D在反比例函数的图象上,
∴66=1,
∴D(6,1),
∴BD=4﹣1=3,
∴S△ABD=12×3×(6﹣3)=92;
(3)过点A作AE⊥OC,垂足为E,连接AC,
设直线OA的关系式为y=kx,将A(3,2)代入得,k=23,
∴直线OA的关系式为y=23x,
设点C(a,0),把x=a代入y=23x,得:y=23a,
把x=a代入y=6x,得:y=6a,
∴B(a,23a),即BC═23a,
∴D(a,6a),即CD=6a,
∵S△ACD=52,
∴12CD•EC=52,即12×6a×(a﹣3)=52,解得:a=18,
BD=BC﹣CD=23a−6a=353,
故答案为:353.
22.(2020春•江都区期末)在函数的学习中,我们经历了“确定函数表达式﹣﹣画函数图象﹣﹣利用函数图象研究函数性质﹣﹣利用图象解决问题”的学习过程.我们可以借鉴这种方法探究函数y=4x−1的图象性质.
(1)补充表格,并画出函数的图象.
①列表:
x
…
﹣3
﹣1
0
2
3
5
…
y
…
﹣1
﹣2
﹣4
4
1
…
②描点并连线,画图.
(2)观察图象,写出该函数图象的一个增减性特征: 当x>1时,y随x的增大而减小,当x<1时,y随x的增大而减小 ;
(3)函数y=4x−1的图象是由函数y=4x的图象如何平移得到的?其对称中心的坐标为 (1,0) ;
(4)根据上述经验,猜一猜函数y=4x−1+2的图象大致位置,结合图象直接写出y≥3时,x的取值范围
1<x≤5 .
【分析】(1)①利用函数解析式求值即可.
②利用描点法画出函数图象即可.
(2)根据图象解答问题即可.
(3)根据图象解答问题即可.
(4)根据平移的性质解决问题即可.
【解析】(1)①x=3时,y=43−1=2.
②图象如图所示:
(2)当x>1时,y随x的增大而减小,当x<1时,y随x的增大而减小.
故答案为:当x>1时,y随x的增大而减小,当x<1时,y随x的增大而减小.
(3)函数y=4x−1的图象是由函数y=4x的图象向右平移1个单位得到.y=4x−1的对称中心为(1,0).
故答案为(1,0)
(4)数y=4x−1+2的图象是由y=4x−1的图象向上平移2个得到,y≥3时,1<x≤5.
故答案为1<x≤5.
23.(2020春•邳州市期末)在平面直角坐标系中,一次函数y=kx+b的图象与反比例y=mx的图象相交于A(3,5)、B(a,﹣3)两点,与x轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)若点P为y轴上的动点,当PB+PC取最小值时,求△BPC的面积.
【分析】(1)利用待定系数法,即可得到反比例函数和一次函数的解析式;
(2)根据一次函数y=x+2,求得C的坐标,即可求得C点关于y轴的对称点C′的坐标,根据待定系数法求得直线BC′的解析式,即可求得P的坐标,然后根据S△BPC=S△BCC′﹣S△PCC′求得即可.
【解析】(1)把A(3,5)代入y=mx可得m=3×5=15,
∴反比例函数的解析式为y=15x;
把点B(a,﹣3)代入y=15x,可得a=﹣5,
∴B(﹣5,﹣3).
把A(3,5),B(﹣5,﹣3)代入y=kx+b,可得3k+b=5−5k+b=−3,
解得k=1b=2,
∴一次函数的解析式为y=x+2;
(2)一次函数的解析式为y=x+2,令y=0,则x=﹣2,
∴C(﹣2,0),
作C点关于y轴的对称点C′,则C′(2,0),即CC=4,
连接B、C′交y轴于P,此时PA+PB有最小值,
设直线BC′的解析式为y=k′x+b′,
∴−5k'+b'=−32k'+b'=0,解得k'=37b'=−67,
则BC′的解析式为y=37x−67,
∴P(0,−67),即OP=67,
∴S△BPC=S△BCC′﹣S△PCC′=12×4×3−12×4×67=307.
24.(2020春•沭阳县期末)已知反比例函数y=kx的图象经过点A(3,n)和B(1,n﹣1).点P(x1,y1)和Q(x2,y2)也在比反比例函数的图象上,且x1<x2.
(1)求n和k的值;
(2)试比较y1与y2的大小.
【分析】(1)将点A(3,n)和B(1,n﹣1)代入反比例函数y=kx即可求n和k的值;
(2)根据点P(x1,y1)和Q(x2,y2)在比反比例函数的图象上,且x1<x2.代入可得y1和y2,进而根据作差法比较y1与y2的大小.
【解析】(1)将点A(3,n)和B(1,n﹣1)代入反比例函数y=kx,
3n=k1×(n−1)=k,
解得n=−12k=−32,
答:n和k的值分别为:−12,−32;
(2)由(1)得,反比例函数解析式为:y=−32x=−32x,
∵点P(x1,y1)和Q(x2,y2)也在比反比例函数的图象上,
∴y1=−32x1,y2=−32x2,
∴y1﹣y2=−32x1+32x2,=32(x1−x2)x1x2,
∵x1<x2.
∴32(x1﹣x2)<0,
∴当x1<x2<0或0<x1<x2时,x1x2>0,
∴y1﹣y2=32(x1−x2)x1x2<0,
即y1<y2;
当x1<0<x2时,x1x2<0,
∴y1﹣y2=32(x1−x2)x1x2>0,
即y1>y2.
苏科版八年级下册9.4 矩形、菱形、正方形课堂检测: 这是一份苏科版八年级下册9.4 矩形、菱形、正方形课堂检测,文件包含专题99正方形-2021-2022学年八年级数学下册尖子生同步培优题典解析版苏科版docx、专题99正方形-2021-2022学年八年级数学下册尖子生同步培优题典原卷版苏科版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
初中数学苏科版八年级下册第9章 中心对称图形——平行四边形9.4 矩形、菱形、正方形课后练习题: 这是一份初中数学苏科版八年级下册第9章 中心对称图形——平行四边形9.4 矩形、菱形、正方形课后练习题,文件包含专题98菱形的判定-2021-2022学年八年级数学下册尖子生同步培优题典解析版苏科版docx、专题98菱形的判定-2021-2022学年八年级数学下册尖子生同步培优题典原卷版苏科版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
初中数学苏科版八年级下册9.4 矩形、菱形、正方形一课一练: 这是一份初中数学苏科版八年级下册9.4 矩形、菱形、正方形一课一练,文件包含专题97菱形的性质-2021-2022学年八年级数学下册尖子生同步培优题典解析版苏科版docx、专题97菱形的性质-2021-2022学年八年级数学下册尖子生同步培优题典原卷版苏科版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。













