华师大版九年级下册3. 切线图文课件ppt

这是一份华师大版九年级下册3. 切线图文课件ppt，文件包含课时1切线的判定和性质定理pptx、电子教案课时1切线的判定和性质定理doc等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
切线的判定切线的性质.（重点、难点）
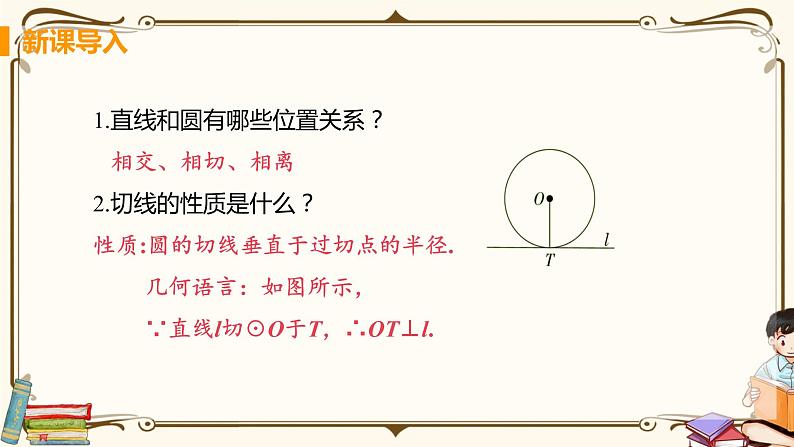
1.直线和圆有哪些位置关系？ 相交、相切、相离2.切线的性质是什么？性质:圆的切线垂直于过切点的半径. 几何语言：如图所示， ∵直线l切☉O于T，∴OT⊥l.
知识点1 切线的判定
　　如图，在⊙O中，经过半径 OA 的外端点 A 作直线 l⊥OA，则圆心 O 到直线 l 的距离是多少？直线 l 和⊙O 有什么位置关系？
经过半径的外端并且垂直于这条半径的直线是圆的切线．
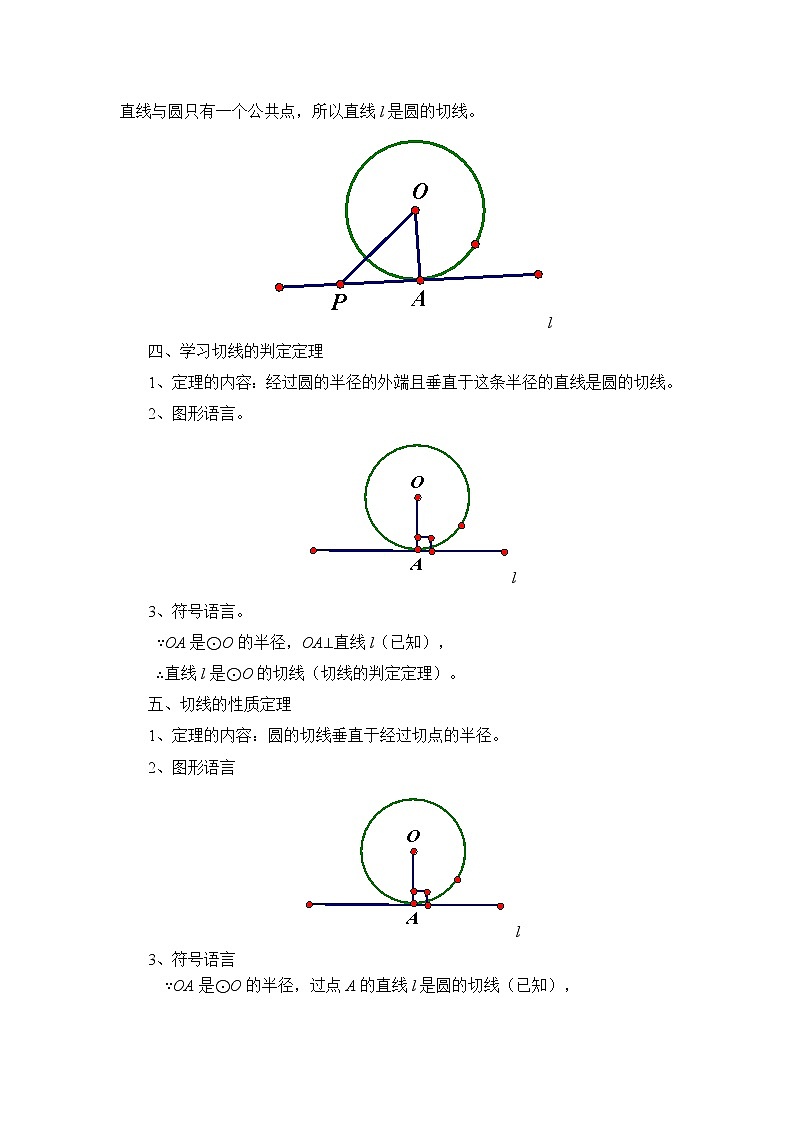
1. 判定定理：经过圆的半径的外端且垂直于这条半径的直 线是圆的切线． 要点精析：切线必须同时具备两个条件：(1)直线过半径的外端；(2)直线垂直于半径．2. 判定方法：(1)定义法：与圆有唯一公共点的直线是圆的切线； (2)数量法：圆心到直线的距离等于半径的直线是圆的切线；(3)判定定理：经过半径的外端并且垂直于这条半径的直线是 圆的切线．
3. 切线判定常用的证明方法：(1)有切点，连半径，证垂直： 如果已知直线经过圆上的一点，那么连结这点和圆心，得到 辅助半径，再证明所作半径与这条直线垂直即可，简记为： 有切点，连半径，证垂直．(2)无切点，作垂直，证半径： 如果已知条件中不知道直线与圆是否有公共点，那么过圆心 作直线的垂线段，再证明垂线段的长度等于半径即可，简记 为：无切点，作垂直，证半径．
如图，已知AB 是⊙ O 的直径，AB=4， 点C 在线段AB 的延长线上， 点D 在⊙ O 上， 连接CD， 且CD=OA，OC=2 ，求证：CD 是⊙ O 的切线.
分析：利用“有切点，连半径，证垂直”判定圆的切线.
证明：连接OD.由题意可知CD=OD=OA= AB=2.∵ OC=2 ，∴ OD2+CD2=OC2.∴∠ ODC=90°，即OD ⊥ CD.又点D 在⊙ O 上，∴ CD 是⊙ O 的切线.
1.下列四个命题：①与圆有公共点的直线是圆的切线；②垂直于圆的半径的直线是圆的切线；③到圆心的距离等于半径的直线是圆的切线；④过直径端点，且垂直于此直径的直线是圆的切线．其中是真命题的是(　　)A．①② B．②③ C．③④ D．①④
2.如图，△ABC是⊙O的内接三角形，下列选项中，能使过点A的直线EF与⊙O相切于点A的条件是(　　)A．∠EAB＝∠C B．∠EAB＝∠BACC．EF⊥AC D．AC是⊙O的直径
知识点2 切线的性质
前面我们已学过的切线的性质有哪些？
答：①切线和圆有且只有一个公共点； ②切线和圆心的距离等于半径.
切线的性质定理：圆的切线垂直于过切点的半径.
如图所示，AB 为⊙ O 的直径，PD 切⊙ O 于点C，交AB 的延长线于点D，且∠ D=2 ∠ CAD.（1）求∠ D 的度数.（2）若CD=2，求BD 的长.
（1）连接OC. ∵ AO=CO，∴∠ OAC= ∠ ACO. ∴∠ COD=2 ∠ CAD.又∵∠ D=2 ∠ CAD，∴∠ D= ∠ COD.∵ PD 与⊙ O 相切于点C，∴ OC ⊥ PD，即∠ OCD=90° .∴∠ D=45° .（2）由（1）可知△ OCD 是等腰直角三角形. ∴ OC=CD=2.由勾股定理，得OD= = =2 ，∴ BD=OD-OB=2 -2.
1.下列说法正确的是(　　)A．圆的切线垂直于半径B．垂直于切线的直线经过圆心C．经过圆心且垂直于切线的直线经过切点D．经过切点的直线经过圆心
2.如图，直线l是⊙O的切线，A为切点，B为直线l上一点，连接OB交⊙O于点C.若AB＝12，OA＝5，则BC的长为(　　)A．5 B．6 C．7 D．8
1.证明直线与圆相切有如下三种途径：(1)定义法：和圆有且只有一个公共点的直线是圆的 切线．(2)数量法(d＝r)：圆心到直线的距离等于半径的 直线是圆的切线．(3)判定定理：经过半径的外端并且垂直于这条半径 的直线是圆的切线．
2.作辅助线的两种方法：(1)若直线与圆的公共点未指明，则过圆心作直线的垂线段， 然后说明这条垂线段的长等于圆的半径；即“作垂直， 证半径”．(2)若直线与圆的一个公共点已指明，则连结这点和圆心， 说明直线垂直于经过这点的半径；即“连半径，证垂直”．3.切线的性质定理：圆的切线垂直于过且点的半径。4.已知直线满足：①过圆心；②过切点；③垂直于切线中的 任意两个，就可得到第三个．
1.如图，AB是⊙O的直径，线段BC与⊙O的交点D是BC的中点，DE⊥AC于点E，连接AD，则下列结论中正确的个数是(　　) ①AD⊥BC；②∠EDA＝∠B；③OA＝ AC；④DE是⊙O的切线．A．1 B．2C．3 D．4
2.如图，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连接BD，AD.若∠ACD＝30°，则∠DBA的大小是(　　)A．15° B．30° C．60° D．75°
如图，点O为∠MPN的平分线上一点，以点O为圆心的⊙O与PN相切于点A. 求证：PM为⊙O的切线．