人教版八年级下册18.2.3 正方形课后练习题

这是一份人教版八年级下册18.2.3 正方形课后练习题，共50页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
专题 18.2.3 正方形（基础篇）（专项练习）
一、单选题
1．如图，四边形ABCD是平行四边形，下列结论中错误的是（ ）

A．当▱ABCD是矩形时，∠ABC＝90° B．当▱ABCD是菱形时，AC⊥BD
C．当▱ABCD是正方形时，AC＝BD D．当▱ABCD是菱形时，AB＝AC
2．如图，正方形ABCD外侧作等边三角形ADE，则∠AEB的度数为（ ）

A．30° B．20° C．15° D．10°
3．如图，四边形是正方形，O，D两点的坐标分别是，，点C在第一象限，则点C的坐标是（ ）

A． B． C． D．
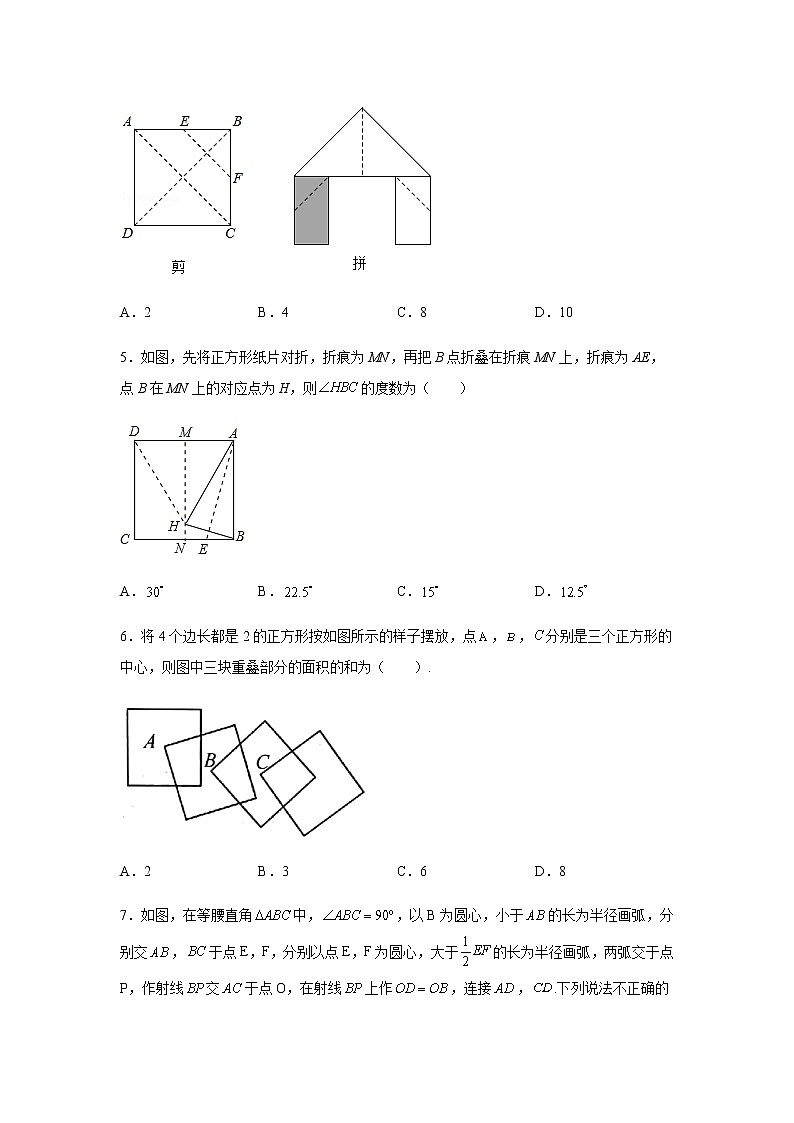
4．如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如图的一座“小别墅”，则图中阴影部分的面积是（　　）

A．2 B．4 C．8 D．10
5．如图，先将正方形纸片对折，折痕为MN，再把B点折叠在折痕MN上，折痕为AE，点B在MN上的对应点为H，则的度数为（ ）

A． B． C． D．
6．将4个边长都是2的正方形按如图所示的样子摆放，点，，分别是三个正方形的中心，则图中三块重叠部分的面积的和为（ ）.

A．2 B．3 C．6 D．8
7．如图，在等腰直角中，，以B为圆心，小于的长为半径画弧，分别交，于点E，F，分别以点E，F为圆心，大于的长为半径画弧，两弧交于点P，作射线交于点O，在射线上作，连接，.下列说法不正确的是（ ）

A． B． C． D．若四边形的周长为16，则
8．下列命题是假命题的是（ ）
A．对角线互相垂直且相等的平行四边形是正方形． B．对角线互相垂直的矩形是正方形．
C．对角线相等的菱形是正方形． D．对角线互相垂直平分的四边形是正方形．
9．已知四边形是平行四边形，下列结论中不正确的是（ ）
A．当时，它是菱形 B．当时，它是正方形
C．当时，它是矩形 D．当时，它是菱形
10．在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（　　）
A．AC＝BD，AB∥CD，AB＝CD B．AD∥BC，∠A＝∠C
C．AO＝BO＝CO＝DO，AC⊥BD D．AO＝CO，BO＝DO，AB＝BC
11．已知菱形ABCD与线段AE，且AE与AB重合．现将线段AE绕点A逆时针旋转180°，在旋转过程中，若不考虑点E与点B重合的情形，点E还有三次落在菱形ABCD的边上，设∠B=α，则下列结论正确的是(　　)
A． B． C． D．
12．如图，在正方形ABCD中，△BPC是等边三角形，BP，CP的延长线分别交AD于点E，F，连接BD，DP，BD与CF交于点H．下列结论：①BE=2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2=PH•PC，其中正确的结论是

A．①②③④ B．②③ C．①②④ D．①③④
13．如图，点P是边长为2cm的正方形ABCD的边上一动点，O是对角线的交点，当点P由A→D→C运动时，设DP＝xcm，则△POD的面积y(cm2)随x(cm)变化的关系图象为( )

A． B．
C． D．
14．如图，在边长为8的正方形中，、分别是边、上的动点，且，为中点，是边上的一个动点，则的最小值是（ ）

A．10 B． C． D．
15．顺次连接矩形ABCD各边的中点，所得四边形必定是（ ）
A．邻边不等的平行四边形 B．矩形
C．正方形 D．菱形
16．下面各图中，所有大正方形边长是，所有小正方形边长是.下面各图中阴影部分面积最大的是( )
A． B． C． D．
17．如图，正方形的两边在坐标轴上，，，点P为OB上一动点，的最小值是（ ）

A．8 B．10 C． D．
18．如图，在菱形ABCD中，AB=4，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（ ）

A．2 B．2 C．4 D．2+2
19．将矩形ABCD按如图所示的方式折叠，BE，EG，FG为折痕，若顶点A，C，D都落在点O处，且点B，O，G在同一条直线上，同时点E，O，F在另一条直线上，则下列说法：①AE＝DE；②EG＞GC；③BE＝BF；④若AB＝1，则AD＝，正确的有（　　）

A．①②③ B．①②④ C．①③④ D．①②③④


二、填空题
20．如图，以边长为2的正方形的中心O为端点，引两条相互垂直的射线，分别与正方形的边交于A、B两点，则线段AB长度的最小值为_________．

21．如图，在正方形ABCD中，点O在内，，则的度数为______．

22．已知正方形ABCD的对角线AC＝，则正方形ABCD的面积为_____．
23．如图，菱形ABCD中，∠B＝60°，AB＝3，四边形ACEF是正方形，则EF的长为_____．

24．如图，将正方形纸片折叠，使点D落在边点E处，点A落在点F处，折痕为，若_____．

25．如图，两个边长为a的正方形重叠，其中一个的顶点在另一个的对角线的交点上，则重叠部分的面积为___________________平方单位．

26．如图，在正方形，E是对角线上一点，的延长线交于点F，连接．若，则______．

27．用两个全等的直角三角形拼下列图形：
①平行四边形（非菱形、矩形和正方形）;
②矩形;
③正方形;
④等腰三角形.
一定可以拼成的图形是_________.(把所有符合条件的图形的序号都写上)
28．如图，中，交于，交于，是的角平分线，那么四边形的形状是________形；在前面的条件下，若再满足一个条件________，则四边形是正方形．

29．对下列现象中蕴含的数学原理阐述正确的是_____（填序号）

①如图（1），剪两张对边平行的纸条，随意交叉叠放在一起，重合的部分构成一个平行四边形．其依据是两组对边分别平行的四边形是平行四边形．
②如图（2），工人师傅在做矩形门窗时，不仅测量出两组对边的长度是否相等，还要测量出两条条对角线的长度相等，以确保图形是矩形．其依据是对角线相等的四边形是矩形．
③如图（3），将两张等宽的纸条放在一起，重合部分构成的四边形ABCD一定是菱形．其依据是一组邻边相等的平行四边形是菱形．
④如图（4），把一张长方形纸片按如图方式折一下，就可以裁出正方形．其依据是一组邻边相等的矩形是正方形．
30．如图，点P是正方形ABCD内位于对角线AC下方的一点，∠1＝∠2，则∠BPC的度数为_____°．

31．如图，在矩形纸片ABCD中，AB＝4，BC＝4，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A'EF，连接A'C，A'D，则当△A'DC是以A'D为腰的等腰三角形时，FD的长是_____．

32．如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是______．

33．如图，矩形纸片ABCD中，，．现将其沿AE对折，使得点B落在边AD上的点处，折痕与边BC交于点E，则的长为___________（cm）．

34．如图所示,在四边形ABCD中，对角线AC⊥BD，垂足为O,点E，F，G,H分别为边AD，AB，BC，CD的中点.若AC＝8，BD＝6,则四边形EFGH的面积为____．

35．如图，在菱形中，，，点，同时由，两点出发，分别沿，方向向点匀速运动，点的运动速度为，点的运动速度为，点到达点后，点与点同时停止运动．若运动时间为秒时，为等边三角形，则的值为__________．

36．如图，在中，，，，点E为边上的一个动点，连接，， 以、为邻边构造，连接，则的最小值为__________．

37．如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8，四边形DHOG面积为（　）

A．6 B．7 C．8 D．9

三、解答题
38．如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE，
（1）求证：四边形AEBD是矩形；
（2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．










39．如图，四边形ABCD是正方形，M为BC上一点，连接AM，延长AD至点E，使得AE=AM，过点E作EF⊥AM，垂足为F，求证：AB=EF．






40．如图所示，已知平行四边形ABCD，对角线AC，BD相交于点O，∠OBC＝∠OCB．
（1）求证：平行四边形ABCD是矩形；
（2）请添加一个条件使矩形ABCD为正方形．






41．如图，在四边形纸片 ABCD 中，∠B＝∠D＝90°，点 E，F 分别在边 BC，CD 上，将 AB，AD 分别沿 AE，AF 折叠，点 B，D 恰好都和点 G 重合，∠EAF＝45°．

（1）求证：四边形 ABCD 是正方形；
（2）若 EC＝FC＝1，求 AB 的长度．




参考答案
1．D
【分析】
由矩形的四个角是直角可判断A，由菱形的对角线互相垂直可判断B，由正方形的对角线相等可判断C，由菱形的四条边相等可判断D，从而可得答案.
【详解】
解：当▱ABCD是矩形时，∠ABC＝90°，正确，故A不符合题意；
当▱ABCD是菱形时，AC⊥BD，正确，故B不符合题意；
当▱ABCD是正方形时，AC＝BD，正确，故C不符合题意；
当▱ABCD是菱形时，AB＝BC，故D符合题意；
故选D
【点拨】本题考查的是矩形，菱形，正方形的性质，熟练的记忆矩形，菱形，正方形的性质是解本题的关键.
2．C
【分析】
根据正方形、等边三角形和三角形内角和定理可以得到答案．
【详解】
四边形是正方形，
，，
是等边三角形，
，，
，，
，
故选：C．
【点拨】本题考查正方形、等边三角形和三角形内角和定理的综合应用，灵活运用有关性质求解是解题关键．
3．D
【分析】
利用O，D两点的坐标，求出OD的长度，利用正方形的性质求出ＯB，BC的长度，进而得出C点的坐标即可．
【详解】
解：∵O，D两点的坐标分别是，，
∴OD＝6，
∵四边形是正方形，
∴OB⊥BC，OB=BC=6
∴C点的坐标为：，
故选：D．
【点拨】本题主要考查了点的坐标和正方形的性质，正确求出OB，BC的长度是解决本题的关键．
4．B
【详解】
解：根据题意，“小别墅”的上面是一个等腰三角形，它的面积是正方形ABCD的一半，而“小别墅”的下面的面积是正方形ABCD的一半，并且下面是两个相等的矩形，
所以图中阴影部分的面积是正方形ABCD面积的
即阴影部分的面积=
考点：正方形
点评：本题考查正方形，解答本题的关键是通过审题，弄清楚阴影部分的面积与正方形面积之间的关系，考生要善于观察
5．C
【分析】
由翻折的性质得到AH=AB，MN垂直平分AD，证明△ADH是等边三角形，得到∠DAH，可得∠HAB，结合AB=AH计算出∠ABH，从而可得∠HBC．
【详解】
解：由翻折的性质可知：AH=AB，MN垂直平分AD，
∴DH=AH，
∴AH=AD=DH=AB，
∴△ADH是等边三角形，
∴∠DAH=60°．
∴∠HAB=30°．
∵AB=AH，
∴∠ABH=×（180°-30°）=75°．
∴∠HBC=15°．
故选C．
【点拨】本题主要考查的是翻折的性质、线段垂直平分线的性质、等边三角形的性质和判定、等腰三角形的性质，证得三角形ADH是一个等边三角形是解题的关键．
6．B
【分析】
如图：连接AP，AN，点A是正方形的对角线的交点，易证≌，可得的面积是正方形的面积的，即每个阴影部分的面积都等于正方形面积的，即可解答.
【详解】
解：如图，

连接AP，AN，点A是正方形的对角线的交点，
则，，
，
，
≌，
四边形AENF的面积等于的面积，
而的面积是正方形的面积的，而正方形的面积为4，
四边形AENF的面积为，三块阴影面积的和为．
故选B．
【点拨】本题主要考查了正方形的特性及面积公式，由图形的特点可知，每个阴影部分的面积都等于正方形面积的，据此解题解答本题的关键是发现每个阴影部分的面积都等于正方形面积的．
7．D
【分析】
根据作图过程可以得出四边形ABCD为正方形，根据正方形的性质逐项判断即可.
【详解】
由作法可知平分，
∴.
∵为等腰直角三角形，
∴.
∴，.
又∵，
∴四边形是菱形.
又∵，
∴四边形是正方形.
∴，.
∵四边形的周长为16，
∴.
∴.
故选D.
【点拨】本题考查了尺规作图，正方形的判定和性质，关键是由作图过程得出判定的条件.
错因分析 中等题.失分的原因是：1.没有掌握基本的尺规作图；2.不能根据角平分线性质，等腰直角三角形性质推导出四边形为正方形.
8．D
【分析】
根据正方形的各种判定方法逐项分析即可．
【详解】
解：对角线互相垂直且相等的平行四边形是正方形，正确；
对角线互相垂直的矩形是正方形，正确；
对角线相等的菱形是正方形，正确；
对角线互相垂直平分且相等的四边形是正方形；
可知选项D是错误的．
故选：D．
【点拨】本题主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．

9．B
【分析】
根据菱形、正方形、矩形的判定方法一一判断即可．
【详解】
解：A、正确．根据邻边相等的平行四边形是菱形；
B、错误．对角线相等的四边形是矩形，不一定是正方形．
C、正确．有一个角是直角的平行四边形是矩形．
D、正确．对角线垂直的平行四边形是菱形．
故选：B．
【点拨】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握，属于基础题．
10．C
【详解】
试题分析：根据正方形的判定：对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案．
解：A，不能，只能判定为矩形；
B，不能，只能判定为平行四边形；
C，能；
D，不能，只能判定为菱形．
故选C．
11．C
【解析】
【分析】
通过临界值的情况结合图形分析，可知当60°<