











初中数学北师大版九年级下册9 弧长及扇形的面积图片ppt课件
展开同学们,你参加过田径运动会吗?为什么在田径200米比赛中,每位运动员的起跑位置不相同呢?
因为每个运动员所跑的弯道的路线是一条弧,而他们各自的半径不相等,所以他们的起跑位置不相同.
【问题】 怎么才能求出弧的长度呢?
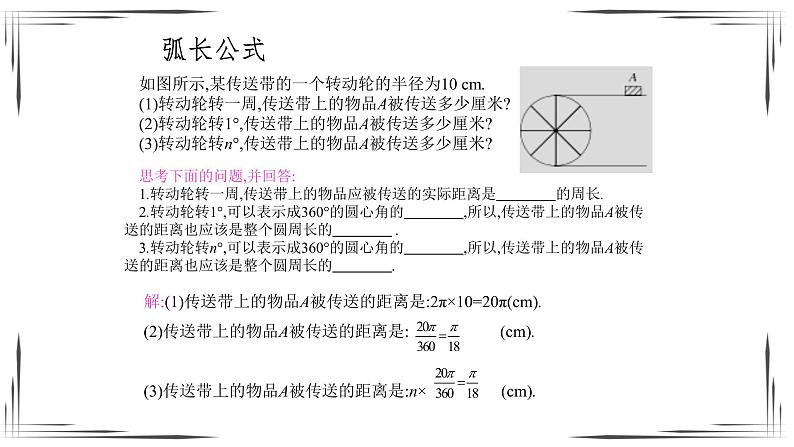
如图所示,某传送带的一个转动轮的半径为10 cm.(1)转动轮转一周,传送带上的物品A被传送多少厘米?(2)转动轮转1°,传送带上的物品A被传送多少厘米?(3)转动轮转n°,传送带上的物品A被传送多少厘米?
思考下面的问题,并回答:1.转动轮转一周,传送带上的物品应被传送的实际距离是 的周长. 2.转动轮转1°,可以表示成360°的圆心角的 ,所以,传送带上的物品A被传送的距离也应该是整个圆周长的 . 3.转动轮转n°,可以表示成360°的圆心角的 ,所以,传送带上的物品A被传送的距离也应该是整个圆周长的 .
解:(1)传送带上的物品A被传送的距离是:2π×10=20π(cm).(2)传送带上的物品A被传送的距离是: (cm).(3)传送带上的物品A被传送的距离是:n× (cm).
【问题】 根据上面的计算,你能探讨出在半径为R的圆中,n°的圆心角所对的弧长的计算公式吗?
分析:360°的圆心角对应圆周长为2πR,那么1°的圆心角对应的弧长为 ,n°的圆心角对应的弧长应为1°的圆心角对应的弧长的n倍,即n× .
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为:l= .
【强调】 弧长的计算公式l= 中的n表示的是1°的圆心角的倍数,所以没有单位.
∴ ×40π≈76.8(mm).因此,管道的展直长度约为76.8 mm.
〔解析〕 管道的展直长度即弧AB的长,已知R=40 mm,n=110,根据弧长公式l= 可求得AB 的长.
制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即 AB 的长(结果精确到0.1 mm).
解:∵R=40 mm,n=110.
在一块空旷的草地上有一根柱子,柱子上拴着一条长3 m的绳子,绳子的另一端拴着一只狗. (1)这只狗的最大活动区域有多大? (2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?
解:(1)这只狗的最大活动区域是圆,它的面积为:32π=9π(m2).
(2)狗的活动区域是扇形(如图(2)所示),扇形是圆的一部分,360°的圆心角对应的圆面积是9π,1°的圆心角对应圆面积的 ,即 ,n°的圆心角对应的圆面积为 .
【点评】 如果圆的半径为R,那么圆的面积为πR2,1°的圆心角对应的扇形面积为 ,n°的圆心角对应的扇形面积为 扇形的面积公式:S= .
比较弧长公式和扇形的面积公式有什么相同点和不同点.它们之间存在什么关系?
解:∵l= ,S扇形= πR2,∴ = .∴S扇形= lR.
扇形面积的计算公式:1.S= πR2;2.S扇形= lR.
扇形AOB的半径为12 cm,∠AOB=120°,求 的长(结果精确到0.1 cm)和扇形AOB的面积(结果精确到0.1 cm2).
〔解析〕 分别利用弧长公式l= πR和扇形的面积公式S= πR2,把已知数据代入即可求AB 的长和扇形AOB的面积.等学生完成后,教师出示解题过程,规范他们的步骤.
解: AB的长= π×12=8π≈25.1(cm).S扇形= π×122≈150.7(cm2).因此, AB 的长约为25.1 cm,扇形AOB的面积约为150.7 cm2.
1.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( ) A. B.2π C.3π D.12π
解析:根据弧长公式可得l= =3π.故选C.
2.如图所示,半径为1的圆中,圆心角为120°的扇形面积为( )
A. B. C. π D. π
解析:由扇形面积公式得S= .故选C.
解析:设圆的半径为x cm,由题意得 ,解得x=6.故填6.
3.150°的圆心角所对的弧长是5π cm,则此弧所在圆的半径是 cm.
4.如图所示,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为 (结果保留π).
解析:S扇形= , S△AOB= ×2×2=2,则S阴影=S扇形-S△AOB=π-2.故填π-2.
5.如图(1)所示,AB是☉O的直径,且AB=4,AC是弦,∠CAB=40°,求劣弧BC和弦AC的长.(弧长计算结果保留π,弦长精确到0.01)
解:连接OC,BC,如图(2)所示,∵∠CAB=40°,∴∠COB=80°,∴劣弧BC的长= ,∵AB为直径,∴∠ACB=90°,在Rt△ACB中,cs 40°= ,∴AC=4cs 40°≈4×0.766≈3.06.
初中数学北师大版九年级下册第三章 圆9 弧长及扇形的面积备课ppt课件: 这是一份初中数学北师大版九年级下册第三章 圆9 弧长及扇形的面积备课ppt课件,文件包含39弧长及扇形的面积pptx、39弧长及扇形的面积doc等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
九年级下册9 弧长及扇形的面积教课ppt课件: 这是一份九年级下册9 弧长及扇形的面积教课ppt课件,共9页。
初中数学北师大版九年级下册9 弧长及扇形的面积课前预习ppt课件: 这是一份初中数学北师大版九年级下册9 弧长及扇形的面积课前预习ppt课件,文件包含39弧长及扇形的面积pptx、北师大版中学数学九年级下册第三章圆39弧长及扇形的面积教学详案docx、北师大版数学九年级下册第三章第9节练练基础题docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。













