初中数学人教版七年级下册5.1.2 垂线导学案

5.1.2  垂 线（知识讲解）

【学习目标】

1. 理解垂直作为两条直线相交的特殊情形，掌握垂直的定义及性质；
2. 理解并运用“垂线段最短”解决实际问题；

3.理解点到直线的距离的概念，并会度量点到直线的距离；

4.能依据对顶角、邻补角及垂直的概念与性质，进行简单的计算.

【要点梳理】

1．垂线的定义：两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫垂足．

特别说明：

(1)记法：直线a与b垂直，记作：；

         直线AB和CD垂直于点O，记作：AB⊥CD于点O.

(2) 垂直的定义具有二重性，既可以作垂直的判定，又可以作垂直的性质，即有：

CD⊥AB．

2．垂线的画法：过一点画已知直线的垂线，可通过直角三角板来画，具体方法是使直角三角板的一条直角边和已知直线重合，沿直线左右移动三角板，使另一条直角边经过已知点，沿此直角边画直线，则所画直线就为已知直线的垂线(如图所示)．

特别说明：

 (1)如果过一点画已知射线或线段的垂线时，指的是它所在直线的垂线，垂足可能在射线的反向延长线上，也可能在线段的延长线上．

(2)过直线外一点作已知直线的垂线，这点与垂足间的线段为垂线段．

3．垂线的性质：

（1）在同一平面内，过一点有且只有一条直线与已知直线垂直．

（2）连接直线外一点与直线上各点的所有线段中，垂线段最短．简单说成：垂线段最短．

特别说明：

（1）性质（1）成立的前提是在“同一平面内”，“有”表示存在，“只有”表示唯一，“有且只有”说明了垂线的存在性和唯一性．

（2）性质（2）是“连接直线外一点和直线上各点的所有线段中，垂线段最短．”实际上，连接直线外一点和直线上各点的线段有无数条，但只有一条最短，即垂线段最短．在实际问题中经常应用其“最短性”解决问题．

4．点到直线的距离：

定义：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．

特别说明：

（1） 点到直线的距离是垂线段的长度，是一个数量，不能说垂线段是距离；

（2）求点到直线的距离时，要从已知条件中找出垂线段或画出垂线段，然后计算或度量垂线段的长度．

【典型例题】

类型一、垂线定义的理解 

1．【答案】130°或50°

【分析】作图分析，若两个角的边互相垂直，那么这两个角必相等或互补，可据此解答．

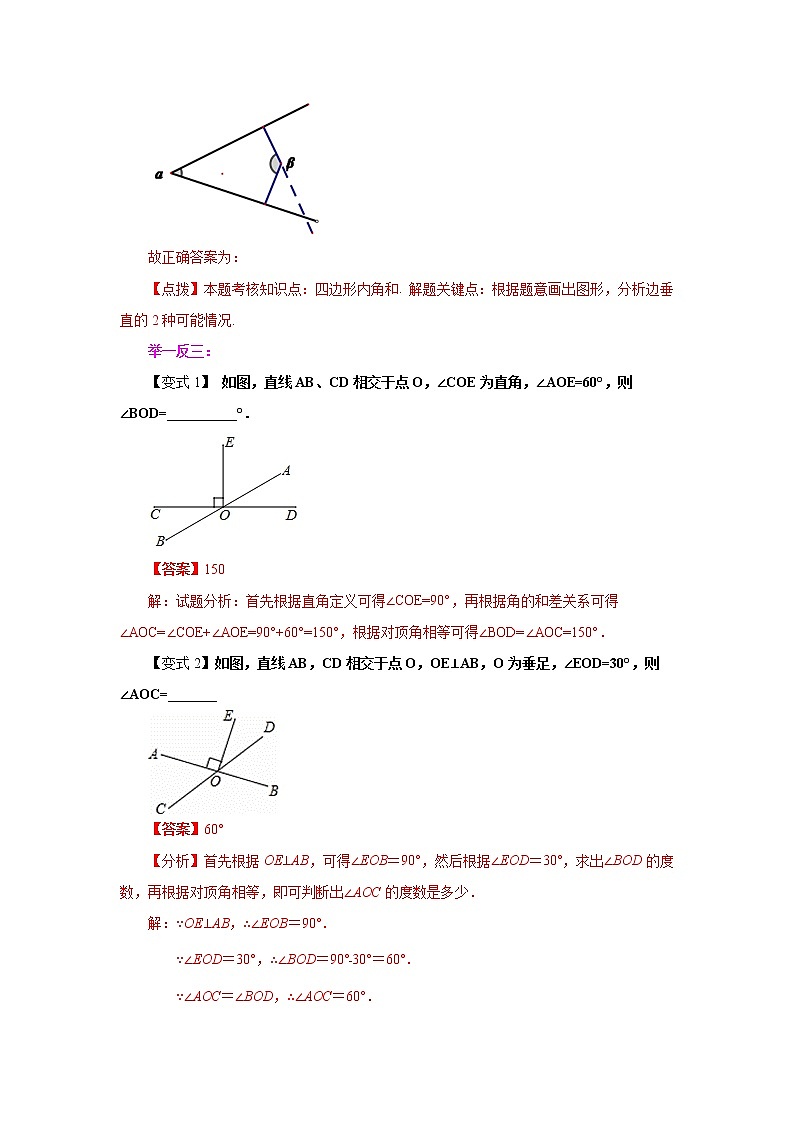
解：如图∵β的两边与α的两边分别垂直，

∴α+β=180°

故β=130°，

在上述情况下，若反向延长∠β的一边，那么∠β的补角的两边也与∠α的两边互相垂直，故此时∠β=50；

综上可知：∠β=50°或130°，

故正确答案为：

【点拨】本题考核知识点：四边形内角和. 解题关键点：根据题意画出图形，分析边垂直的2种可能情况.

举一反三：

【变式1】 如图，直线AB、CD相交于点O，∠COE为直角，∠AOE=60°，则∠BOD=__________°．

【答案】150

解：试题分析：首先根据直角定义可得∠COE=90°，再根据角的和差关系可得∠AOC=∠COE+∠AOE=90°+60°=150°，根据对顶角相等可得∠BOD=∠AOC=150°．

【变式2】如图，直线AB，CD相交于点O，OE⊥AB，O为垂足，∠EOD=30°，则∠AOC=_______

【答案】60°

【分析】首先根据OE⊥AB，可得∠EOB＝90°，然后根据∠EOD＝30°，求出∠BOD的度数，再根据对顶角相等，即可判断出∠AOC的度数是多少．

解：∵OE⊥AB，∴∠EOB＝90°．

∵∠EOD＝30°，∴∠BOD＝90°﹣30°＝60°．

∵∠AOC＝∠BOD，∴∠AOC＝60°．

故答案为60°．

【点拨】（1）此题主要考查了垂线的性质和应用，要熟练掌握，解答此类问题的关键是要明确：垂线的性质在平面内，过一点有且只有一条直线与已知直线垂直．

（2）此题还考查了对顶角的特征和性质的应用，要熟练掌握，解答此题的关键是要明确：对顶角相等．

类型二、画垂线 

2．如图所示，直线AB，CD相交于点O，P是CD上一点．

（1）过点P画AB的垂线段PE．

（2）过点P画CD的垂线，与AB相交于F点．

（3）说明线段PE，PO，FO三者的大小关系，其依据是什么？

【答案】(1)见解析；（2）见解析；（3）PE＜PO＜FO，其依据是“垂线段最短”

【分析】前两问尺规作图见详解,第（3）问中利用垂线段最短即可解题.

解：（1）（2）如图所示．

（3）在直角△FPO中,PO＜FO,

在直角△PEO中,PE＜PO,

∴PE＜PO＜FO，其依据是“垂线段最短”．

【点拨】本题考查了尺规作图和垂线段的性质,属于简单题,熟悉尺规作图的方法和步骤,垂线段的性质是解题关键.

举一反三：

【变式1】 如图：点C是∠AOB的边OB上的一点，按下列要求画图并回答问题．

（1）过C点画OB的垂线，交OA于点D；

（2）过C点画OA的垂线，垂足为E；

（3）比较线段CE，OD，CD的大小（请直接写出结论）；

（4）请写出第（3）小题图中与∠AOB互余的角（不增添其它字母）．

【答案】(1)见解析；（2）见解析；（3）CE＜CD＜OD；（4）与∠AOB互余的角是∠OCE与∠ODC

【分析】(1)作DC⊥OB即可；

(2)作CE⊥OA即可；

(3)根据垂线段最短及直角三角形的斜边大于任一直角边即可得出结论；

(4)根据两角互余的定义即可得出结论．

解：解：(1)、(2)如图所示；

(3)∵CE⊥OA，

∴CE＜CD.

∵△OCD中OD是斜边，CD是直角边，

∴CD＜OD，

∴CE＜CD＜OD；

(4)  ∵CE⊥OA，

∴∠AOB+∠OCE=90°．

∵CD⊥OB，

∴∠AOB+∠ODC=90°，

∴与∠AOB互余的角是∠OCE与∠ODC．

【点拨】本题考查的是作图-基本作图，熟知垂线的作法是解答此题的关键．

【变式2】如图，，在的内部有一条射线.

（1）画射线

（2）写出此时与的数量关系，并说明理由.

【答案】（1）作图见解析（2）（1）或

【解析】

试题分析：（1）根据基本作图—做已知直线的垂线即可；

（2）通过图形判断即可.

试题解析：（1）画图，如下图

（2）或

类型三、垂线段最短 

3．如图所示，在△ABC中，AC=5，BC=6，BC边上高AD=4，若点P在边AC上（不含端点）移动，求BP最短时的值．

【答案】

【分析】根据点到直线的连线中，垂线段最短，得到当BP垂直于AC时，BP的长最小，利用面积法即可求出此时BP的长．

解：根据垂线段最短可知，当BP⊥AC时，BP最短．

∵S△ABCBC×ADAC×BP，∴6×4=5BP，∴PB，即BP最短时的值为：．

【点拨】本题考查了垂线段最短，熟练掌握垂线段的性质是解答本题的关键．

举一反三：

【变式1】 如图，在直线MN的异侧有A、B两点，按要求画图取点，并注明画图取点的依据．

(1)在直线MN上取一点C，使线段AC最短．依据是______________．

(2)在直线MN上取一点D，使线段AD＋BD最短．依据是______________________．

【答案】垂线段最短    两点之间，线段最短   

【分析】(1)过A作AC⊥MN，AC最短；

(2)连接AB交MN于D，这时线段AD+BD最短．

解：(1)过A作AC⊥MN，根据垂线段最短，

故答案为垂线段最短；

(2)连接AB交MN于D，根据是两点之间线段最短，

故答案为两点之间线段最短．

【点拨】本题主要考查了垂线段的性质和线段的性质，关键是掌握垂线段最短；两点之间线段最短．

【变式2】火车站，码头分别位于A，B两点，直线a，b分别表示铁路与河流．

(1)从火车站到码头怎样走最近？

(2)从码头到铁路怎样走最近？请画图并说明理由．

【答案】（1）详见解析；（2）详见解析.

【分析】(1)从火车站到码头的距离是点到点的距离，即两点间的距离，依据两点之间线段最短解答即可；

(2)从码头到铁路的距离是点到直线的距离，依据垂线段最短解答即可．

解：如图所示

(1)沿AB走，两点之间线段最短；

(2)沿BD走，垂线段最短.

【点拨】本题考查了线段的性质、垂线段的性质，根据具体的问题正确判断出是点到点的距离还是点到线的距离是解答问题的关键．

类型四、点到直线的距离 

4．如图，已知直线AB及直线AB外一点P，按下列要求完成画图和解答：（1）连接PA，PB，用量角器画出∠APB的平分线PC，交AB于点C；

（2）过点P作PD⊥AB于点D；

（3）用刻度尺取AB中点E，连接PE；

（4）根据图形回答：点P到直线AB的距离是线段         的长度．

【答案】（1）答案见解析；（2）答案见解析；（3）答案见解析；（4）PD．

解：试题分析：(1)、用量角器量出∠APB的度数，然后求出一半的度数得出答案；(2)、根据垂线的作法得出答案；(3)、用刻度尺量出AB的长度，然后找出中点，从而得出答案；(4)、点到直线的距离是指点到直线垂线段的长度．

解：(1)、如图所示；(2)、如图所示；(3)、如图所示；

(4)、PD．

举一反三：

【变式1】 如图.

（1）试说出点A到直线BC的距离；点B到直线AC的距离；

（2）点C到直线AB的距离是多少？

【答案】（1）点A到直线BC的距离、点B到直线AC的距离分别是9，12；（2）

【分析】根据点到直线的距离即为垂线段的距离，求解即可.

解：（1）∵，

∴点A到直线BC的距离、点B到直线AC的距离分别是9，12.

（2）设点C到直线AB的距离为h，

的面积为，

∴，

∴.

∴点C到直线AB的距离为.

【点拨】此题主要考查对垂线段的理解，熟练掌握，即可解题.

【变式2】如图，△ABC中，∠A+∠B=900.

⑴根据要求画图：

①过点C画直线MN∥AB

②过点C画AB的垂线，交AB于点D．

⑵请在⑴的基础上回答下列问题：

①已知∠B+∠DCB=900，则∠A与∠DCB的大小关系为__________，理由是__________.

②图中线段_________的长度表示点A到直线CD的距离.

【答案】（1）作图见解析（2）① ；∠A=∠DCB；同角的余角相等；②AD

解：

试题分析：（1）根据题意画出MN∥AB，CD⊥AB于D；

（2）①根据同角的余角相等可判断∠A=∠DCB；

②根据点到直线的距离的定义求解．

试题解析：解：（1）①如图，MN为所求；

②如图，CD为所求；

（2）①∵∠B+∠DCB=90°，∠B+∠A=90°，∴∠A=∠DCB；

②线段AD长度表示点A到直线CD的距离．

故答案为∠A=∠DCB，同角的余角相等；AD．