

考点16相似三角形(解析版)-2022年数学中考一轮复习考点透析(华师大版)
展开考点16相似三角形
考点总结
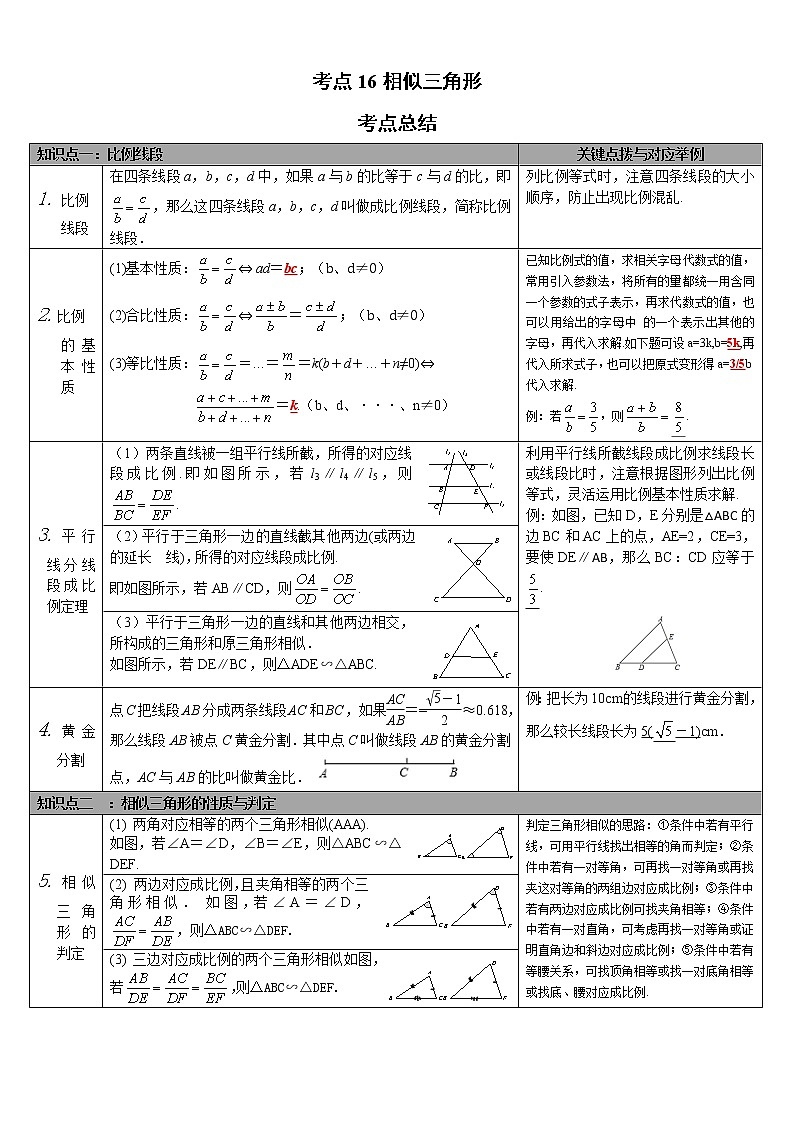
知识点一:比例线段
关键点拨与对应举例
1. 比例
线段
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
列比例等式时,注意四条线段的大小顺序,防止出现比例混乱.
2.比例
的基本性质
(1)基本性质:⇔ ad=bc;(b、d≠0)
(2)合比性质:⇔=;(b、d≠0)
(3)等比性质:=…==k(b+d+…+n≠0)⇔
=k.(b、d、···、n≠0)
已知比例式的值,求相关字母代数式的值,常用引入参数法,将所有的量都统一用含同一个参数的式子表示,再求代数式的值,也可以用给出的字母中 的一个表示出其他的字母,再代入求解.如下题可设a=3k,b=5k,再代入所求式子,也可以把原式变形得a=3/5b代入求解.
例:若,则.
3.平行线分线段成比例定理
(1)两条直线被一组平行线所截,所得的对应线 段成比例.即如图所示,若l3∥l4∥l5,则.
利用平行线所截线段成比例求线段长或线段比时,注意根据图形列出比例等式,灵活运用比例基本性质求解.
例:如图,已知D,E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB,那么BC:CD应等于.
(2)平行于三角形一边的直线截其他两边(或两边的延长 线),所得的对应线段成比例.
即如图所示,若AB∥CD,则.
(3)平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.
如图所示,若DE∥BC,则△ADE∽△ABC.
4.黄金分割
点C把线段AB分成两条线段AC和BC,如果==≈0.618,那么线段AB被点C黄金分割.其中点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.
例:把长为10cm的线段进行黄金分割,那么较长线段长为5(-1)cm.
知识点二 :相似三角形的性质与判定
5.相似三角形的判定
(1) 两角对应相等的两个三角形相似(AAA).
如图,若∠A=∠D,∠B=∠E,则△ABC∽△DEF.
判定三角形相似的思路:①条件中若有平行
线,可用平行线找出相等的角而判定;②条
件中若有一对等角,可再找一对等角或再找
夹这对等角的两组边对应成比例;③条件中
若有两边对应成比例可找夹角相等;④条件
中若有一对直角,可考虑再找一对等角或证
明直角边和斜边对应成比例;⑤条件中若有
等腰关系,可找顶角相等或找一对底角相等
或找底、腰对应成比例.
(2) 两边对应成比例,且夹角相等的两个三角形相似. 如图,若∠A=∠D,,则△ABC∽△DEF.
(3) 三边对应成比例的两个三角形相似.如图,若,则△ABC∽△DEF.
6.相似
三角形的性质
(1)对应角相等,对应边成比例.
(2)周长之比等于相似比,面积之比等于相似比的平方.
(3)相似三角形对应高的比、对应角平分线的比和对应中线的比等于相似比.
例:(1)已知△ABC∽△DEF,△ABC的周长为3,△DEF的周长为2,则△ABC与△DEF的面积之比为9:4.
(2) 如图,DE∥BC, AF⊥BC,已知S△ADE:S△ABC=1:4,则AF:AG=1:2.
7.相似三角形的基本模型
(1)熟悉利用利用相似求解问题的基本图形,可以迅速找到解题思路,事半功倍.
(2)证明等积式或者比例式的一般方法:经常把等积式化为比例式,把比例式的四条线段分别看做两个三角形的对应边.然后,通过证明这两个三角形相似,从而得出结果.
真题演练
一、单选题
1.(2021·山东滨州·中考真题)如图,在中,,点C为边AB上一点,且.如果函数的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(-2019,674) B.(-2020,675)
C.(2021,-669) D.(2022,-670)
【答案】D
【分析】
根据反比例函数图象上点的坐标特征,求出B、C点的坐标,再写出BC解析式,再判断点在BC上.
【详解】
解:作,,
,
,
设,
,
或(舍去),
,
,
.
,
,,
,
,
,
,
图象经过点,
,
,
设的解析式为,
,
解得,
,
当时,,
当时,,
当时,,
当时,,
故选:D.
2.(2021·山东淄博·中考真题)如图,在平面直角坐标系中,四边形的边与轴的正半轴重合,,轴,对角线交于点.已知的面积为4.若反比例函数的图象恰好经过点,则的值为( )
A. B. C. D.12
【答案】B
【分析】
过点M作ME⊥x轴于点E,则有ME∥BD,,进而可得、,然后根据相似三角形的面积比与相似比的关系可进行求解.
【详解】
解:过点M作ME⊥x轴于点E,如图所示:
∵轴,
∴ME∥BD,
∵,
∴,
∵,
∴,
∵的面积为4,
∴,
∵,
∴,
由题可知△OMB、△OBD的高是相同的,则有,
∴,
∵ME∥BD,
∴,
∴,
∴,
由反比例函数k的几何意义可得:,
∵,
∴;
故选B.
3.(2021·山东淄博·中考真题)如图,在中,是斜边上的中线,过点作交于点.若的面积为5,则的值为( )
A. B. C. D.
【答案】A
【分析】
由题意易得,设,则有,则有,,然后可得,过点C作CH⊥AB于点H,进而根据三角函数及勾股定理可求解问题.
【详解】
解:∵,,
∴,
∴,
∵是斜边上的中线,
∴,
设,则有,
∵,
∴由勾股定理可得,
∵的面积为5,
∴,
∵,
∴,即,化简得:,
解得:或,
当时,则AC=2,与题意矛盾,舍去;
∴当时,即,过点C作CH⊥AB于点H,如图所示:
∴,,,
∴,,
∴,
∴,
∴;
故选A.
4.(2021·山东淄博·中考真题)如图,相交于点,且,点在同一条直线上.已知,则之间满足的数量关系式是( )
A. B. C. D.
【答案】C
【分析】
由题意易得,,则有,,然后可得,进而问题可求解.
【详解】
解:∵,
∴,,
∴,,
∴,
∵,
∴,即;
故选C.
5.(2021·山东济宁·中考真题)如图,已知.
(1)以点A为圆心,以适当长为半径画弧,交于点M,交于点N.
(2)分别以M,N为圆心,以大于的长为半径画弧,两弧在的内部相交于点P.
(3)作射线交于点D.
(4)分别以A,D为圆心,以大于的长为半径画弧,两弧相交于G,H两点.
(5)作直线,交,分别于点E,F.
依据以上作图,若,,,则的长是( )
A. B.1 C. D.4
【答案】C
【分析】
连接,则,根据相似三角形对应边成比例即可得出结果
【详解】
如图,连接
垂直平分
,
平分
同理可知
四边形是平行四边形
又
平行四边形是菱形
又
,
解得:
故选C
6.(2021·山东聊城·中考真题)如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1,则点A1的坐标为( )
A.() B.() C.() D.()
【答案】A
【分析】
先求出AB,OA1,再作辅助线构造相似三角形,如图所示,得到对应边成比例,求出OC和A1C,即可求解.
【详解】
解:如图所示,∵点A,B的坐标分别为A(0,2),B(﹣1,0),
∴OB=1,OA=2,
∴,
∵∠AOB=90°,
∴∠A1OB1=90°,
∴O A1⊥OB1,
又∵AB⊥OB1,
∴O A1∥AB,
∴∠1=∠2,
过A1点作A1C⊥x轴,
∴∠A1CO=∠AOB,
∴,
∴,
∵O A1=OA=2,
∴,
∴,,
∴,
故选:A.
7.(2021·山东威海·中考真题)如图,在和中,,,.连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分,则下列结论错误的是( )
A. B. C. D.
【答案】C
【分析】
根据即可证明,再利用全等三角形的性质以及等腰三角形的性质,结合相似三角形的判定和性质,即可一一判断
【详解】
,故选项A正确;
平分
,故选项B正确;
即
,故选项C错误;
,故选项D正确;
故答案选:C.
8.(2021·山东东营·中考真题)如图,是边长为1的等边三角形,D、E为线段AC上两动点,且,过点D、E分别作AB、BC的平行线相交于点F,分别交BC、AB于点H、G.现有以下结论:①;②当点D与点C重合时,;③;④当时,四边形BHFG为菱形,其中正确结论为( )
A.①②③ B.①②④ C.①②③④ D.②③④
【答案】B
【分析】
过A作AI⊥BC垂足为I,然后计算△ABC的面积即可判定①;先画出图形,然后根据等边三角形的性质和相似三角形的性质即可判定②;如图将△BCD绕B点逆时针旋转60°得到△ABN,求证NE=DE;再延长EA到P使AP=CD=AN,证得∠P=60°,NP=AP=CD,然后讨论即可判定③;如图1,当AE=CD时,根据题意求得CH=CD、AG=CH,再证明四边形BHFG为平行四边形,最后再说明是否为菱形.
【详解】
解:如图1, 过A作AI⊥BC垂足为I
∵是边长为1的等边三角形
∴∠BAC=∠ABC=∠C=60°,CI=
∴AI=
∴S△ABC=,故①正确;
如图2,当D与C重合时
∵∠DBE=30°,是等边三角形
∴∠DBE=∠ABE=30°
∴DE=AE=
∵GE//BD
∴
∴BG=
∵GF//BD,BG//DF
∴HF=BG=,故②正确;
如图3,将△BCD绕B点逆时针旋转60°得到△ABN
∴∠1=∠2,∠5=∠6=60°,AN=CD,BD=BN
∵∠3=30°
∴∠2+∠4=∠1+∠4=30°
∴∠NBE=∠3=30°
又∵BD=BN,BE=BE
∴△NBE≌△DBE(SAS)
∴NE=DE
延长EA到P使AP=CD=AN
∵∠NAP=180°-60°-60°=60°
∴△ANP为等边三角形
∴∠P=60°,NP=AP=CD
如果AE+CD=DE成立,则PE=NE,需∠NEP=90°,但∠NEP不一定为90°,故③不成立;
如图1,当AE=CD时,
∵GE//BC
∴∠AGE=∠ABC=60°,∠GEA=∠C=60°
∴∠AGE=∠AEG=60°,
∴AG=AE
同理:CH=CD
∴AG=CH
∵BG//FH,GF//BH
∴四边形BHFG是平行四边形
∵BG=BH
∴四边形BHFG为菱形,故④正确.
故选B.
9.(2021·山东东营·中考真题)如图,中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作的位似图形,并把的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是( )
A. B. C. D.
【答案】A
【分析】
设点的横坐标为,然后表示出、的横坐标的距离,再根据位似比列式计算即可得解.
【详解】
设点的横坐标为,
则、间的横坐标的差为,、间的横坐标的差为,
放大到原来的倍得到,
,
解得:.
故选:A.
10.(2021·山东聊城·中考真题)如图,四边形ABCD中,已知AB∥CD,AB与CD之间的距离为4,AD=5,CD=3,∠ABC=45°,点P,Q同时由A点出发,分别沿边AB,折线ADCB向终点B方向移动,在移动过程中始终保持PQ⊥AB,已知点P的移动速度为每秒1个单位长度,设点P的移动时间为x秒,△APQ的面积为y,则能反映y与x之间函数关系的图象是( )
A. B. C. D.
【答案】B
【分析】
依次分析当、、三种情况下的三角形面积表达式,再根据其对应图像进行判断即可确定正确选项.
【详解】
解:如图所示,分别过点D、点C向AB作垂线,垂足分别为点E、点F,
∵已知AB∥CD,AB与CD之间的距离为4,
∴DE=CF=4,
∵点P,Q同时由A点出发,分别沿边AB,折线ADCB向终点B方向移动,在移动过程中始终保持PQ⊥AB,
∴PQ∥DE∥CF,
∵AD=5,
∴,
∴当时,P点在AE之间,此时,AP=t,
∵,
∴,
∴,
因此,当时,其对应的图像为,故排除C和D;
∵CD=3,
∴EF=CD=3,
∴当时,P点位于EF上,此时,Q点位于DC上,其位置如图中的P1Q1,则,
因此当时,对应图像为,即为一条线段;
∵∠ABC=45°,
∴BF=CF=4,
∴AB=3+3+4=10,
∴当时,P点位于FB上,其位置如图中的P2Q2,此时,P2B=10-x,
同理可得,Q2P2=P2B=10-x,
,
因此当时,对应图像为,其为开口向下的抛物线的的一段图像;
故选:B.
二、填空题
11.(2021·山东青岛·中考真题)已知正方形的边长为3,为上一点,连接并延长,交的延长线于点,过点作,交于点,交于点,为的中点,为上一动点,分别连接,.若,则的最小值为__________.
【答案】
【分析】
由正方形的性质,可得A点与C点关于BD对称,则有MN +CM=MN+AM≥AN,所以当A、M、N三点共线时,MN+CM的值最小为AN,先证明△DCG~△FCE,再由,可得,分别求出DE=1,CE=2,CF=6,即可求出AN.
【详解】
解:∵四边形ABCD是正方形,
∴A点与C点关于BD对称,
∴CM=AM,
∴MN+CM=MN+AM≥AN,
∴当A、M、N三点共线时,MN+CM的值最小,
∵AD∥CF,
∴∠DAE=∠F,
∵∠DAE+∠DEH=90°,
∵DG⊥AF,
∴∠CDG+∠DEH=90°,
∴∠DAE=∠CDG,
∴∠CDG=∠F,
∴△DCG~△FCE,
∵,
∴ ,
∵正方形边长为3,
∴CF=6,
∵AD∥CF,
,
∴DE=1,CE=2,
在Rt△CEF中,EF2=CE2+CF2,
∴ ,
∵N是EF的中点,
,
在Rt△ADE中,EA2=AD2+DE2,
∴ ,
∴ ,
∴MN+MC的最小值为 .
故答案为:.
12.(2021·山东济南·中考真题)如图,一个由8个正方形组成的“”型模板恰好完全放入一个矩形框内,模板四周的直角顶点,,,,都在矩形的边上,若8个小正方形的面积均为1,则边的长为__________.
【答案】
【分析】
如图,延长交于点,连接,根据题意求得的长,设,先证明,再证明,,分别求出矩形的四边,根据矩形对边相等列方程组求得的值,进而求得的值.
【详解】
小正方形的面积为1,则小正方形的边长为,
如图,延长交于点,连接,
,,
四边形是正方形,
,
,
设,
四边形是矩形,
,
,
,
,
,,
,
,,
,
即①
②
联立
解得
故答案为:
13.(2021·山东日照·中考真题)如图,在平面直角坐标系中,正方形的边、分别在轴和轴上,,点是边上靠近点的三等分点,将沿直线折叠后得到,若反比例函数的图象经过点,则的值为_______.
【答案】48
【分析】
过作于,交于,设,,,通过证得△△,得到,解方程组求得、的值,即可得到的坐标,代入即可求得的值.
【详解】
解:过作于,交于,
,
,
,
,
,
△△,
,
设,
,,
正方形的边、分别在轴和轴上,,点是边上靠近点的三等分点,
,,
,
解得,,
,
反比例函数的图象经过点,
,
故答案为48.
14.(2021·山东泰安·中考真题)如图,点在直线上,点的横坐标为2,过点作,交x轴于点,以为边,向右作正方形,延长交x轴于点;以为边,向右作正方形,延长交x轴于点;以为边,向右作正方形,延长的交x轴于点;…;按照这个规律进行下去,则第n个正方形的边长为________(结果用含正整数n的代数式表示).
【答案】
【分析】
根据题中条件,证明所有的直角三角形都相似且确定相似比,再具体算出前几个正方形的边长,然后再找规律得出第个正方形的边长.
【详解】
解:点在直线上,点的横坐标为2,
点纵坐标为1.
分别过,作轴的垂线,分别交于,下图只显示一条;
,
类似证明可得,图上所有直角三角形都相似,有
,
不妨设第1个至第个正方形的边长分别用:来表示,通过计算得:
,
,
按照这个规律进行下去,则第n个正方形的边长为,
故答案是:.
15.(2021·山东东营·中考真题)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若,则GE的长为________.
【答案】
【分析】
因为折叠,则有,从而可知,利用线段比求出DG的长,即可求出EG.
【详解】
如图, 四边形ABCD是正方形,
,
因为折叠,,设垂足为H,
,
,
,
,
,
,,DE=,
,
,
故答案为.
三、解答题
16.(2021·山东青岛·中考真题)已知:如图,在矩形和等腰中,,,.点从点出发,沿方向匀速运动.速度为;同时,点从点出发,沿方向匀速运动,速度为.过点作,交于点,交于点,过点作,交于点.分别连接,,设运动时间为.
解答下列问题:
(1)当时,求的值;
(2)设五边形的面积为,求与之间的函数关系式;
(3)当时,求的值;
(4)若与相交于点,分别连接和.在运动过程中,是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
【答案】(1);(2);(3);(4)存在,
【分析】
(1)先证,得代数计算即可;
(2)如图2中,过点P作PO⊥QM于点O.证明S=S四边形DQPM+S△DNQ=(PQ+DH)•QM+QN•ND=(HA+DH)•QM+QN•ND=•AD•QM+QN•ND,可得结论.
(3)如图3中,延长NQ交BE于点G.根据PQ=PM,构建方程求解即可.
(4)存在.证明△HQW∽△AEW,△MHW∽△PAW,推出,,推出,由此构建方程求解即可
【详解】
(1)由题意可得,,,
在矩形中,
∵,,
,
在中,,
,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
∴.
答:为时,.
(2)过点作,交于点,
在等腰中,
,,
则.
∵,
∴,
∴四边形是矩形,
∴.
∵,
∴,
又∵,
∴,
∴,∴,∴.
∵,∴,
又∵,
∴,
∴,
∴,
∴,.
∴
.
答:与的函数关系式是.
(3)延长交于点,由(1),(2)可得,
,,
∵,
∴四边形是矩形,
∴,
同理可证,四边形是矩形.
∴,
当时,
∵,
∴,
∴.
又∵,
∴,
∴.
答:当时,.
(4)由(2)得,,
∵,,
∴,
∴为矩形,
∴,且.
∴,
∵,
∴,
同理可证,
∴,,
∴,
∴,
∴.
答:在运动的过程中,存在时刻,使.
17.(2021·山东济南·中考真题)如图,直线与双曲线交于,两点,点的坐标为,点是双曲线第一象限分支上的一点,连接并延长交轴于点,且.
(1)求的值并直接写出点的坐标;
(2)点是轴上的动点,连接,,求的最小值;
(3)是坐标轴上的点,是平面内一点,是否存在点,,使得四边形是矩形?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.
【答案】(1),B(2,3);(2);(3)P(,0)或(0,).
【分析】
(1)根据直线经过点A,可求出点A(-2,-3),因为点A在图象上,可求出k,根据点A和点B关于原点对称,即可求出点B;
(2)先根据利用相似三角形的性质求出点C,再根据对称性求出点B关于y轴的对称点B’,连接B’C,即B’C的长度是的最小值;
(3)先作出图形,分情况讨论,利用相似三角形的性质求解即可.
【详解】
(1)解:因为直线经过点,
所以,
所以m=-2,
所以点A(-2,-3),
因为点A在图象上,
所以,
因为与双曲线交于A,两点,
所以点A和点B关于原点对称,
所以点B(2,3);
(2)过点B,C分别作BE⊥x轴,CF⊥x轴,作B关于y轴对称点B’,连接B’C,
因为BE⊥x轴,CF⊥x轴,
所以BE//CF,
所以,
所以,
因为,
所以,
因为B(2,3),
所以BE=3,
所以CF=1,
所以C点纵坐标是1,
将代入可得:x=6,
所以点C(6,1),
又因为点B’是点B关于y轴对称的点,
所以点B’(-2,3),
所以B’C=,
即的最小值是;
(3)解:①当点P在x轴上时,
当∠ABP=90°,四边形ABPQ是矩形时,过点B作BH⊥x轴,
因为∠OBP=90°,BH⊥OP,
所以,
所以,
所以,
所以,
所以,
所以,
所以点P(,0);
②当点P在y轴上时,
当∠ABP=90°,四边形ABPQ是矩形时,过点B作BH⊥y轴,
因为∠OBP=90°,BH⊥OP,
所以,
所以,
所以,
所以,
所以,
所以,
所以点P(0,)
综合可得:P(,0)或(0,).
18.(2021·山东日照·中考真题)已知:抛物线经过,,三点.
(1)求抛物线的解析式;
(2)如图1,点为直线上方抛物线上任意一点,连、、,交直线于点,设,求当取最大值时点的坐标,并求此时的值;
(3)如图2,点为抛物线对称轴与轴的交点,点关于轴的对称点为点.
①求的周长及的值;
②点是轴负半轴上的点,且满足(为大于0的常数),求点的坐标.
【答案】(1)y=-x2+2x+3;(2)k=,P(,);(3)①,;②(0,)或(0,)
【分析】
(1)运用待定系数法即可求得答案;
(2)如图1,过点作轴交直线于点,则,进而可得,再运用待定系数法求得直线的解析式为,设点,则,从而得出,再利用二次函数性质即可得出答案;
(3)①如图2,过点作于点,则,利用配方法求得抛物线对称轴为直线,得出,运用勾股定理即可求得的周长;再证明是等腰直角三角形,利用三角函数求得,,即可求得答案;
②设,则,根据,求得、,再利用,求得,根据,可得,化简得,解方程即可求得答案.
【详解】
解:(1)抛物线经过,,,
设,将代入,得,
解得:,
,
抛物线的解析式为;
(2)如图1,过点作轴交直线于点,
,
,
,,
,
设直线的解析式为,
,,
,
解得:,
直线的解析式为,
设点,则,
,
,
当时,取得最大值,此时,,;
(3)①如图2,过点作于点,则,
,
抛物线对称轴为直线,
,
,,
点关于轴的对称点为点,
,
,
,
,
,
,
的周长;
在中,,,
,
,
是等腰直角三角形,
,
,
;
②设,则,
,
,
,
,
,
,
,
,,
,
,即,
,
,
,
整理得,,
,,
,即,
当△,即时,
,
或.
考点16相似三角形(解析版)-2022年数学中考一轮复习考点透析(苏科版): 这是一份考点16相似三角形(解析版)-2022年数学中考一轮复习考点透析(苏科版),共21页。试卷主要包含了比和比例的有关概念等内容,欢迎下载使用。
考点03分式(解析版)-2022年数学中考一轮复习考点透析(华师大版): 这是一份考点03分式(解析版)-2022年数学中考一轮复习考点透析(华师大版),共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
考点01实数(解析版)-2022年数学中考一轮复习考点透析(华师大版): 这是一份考点01实数(解析版)-2022年数学中考一轮复习考点透析(华师大版),共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












